Kapitel 7 Spezielle Features
7.1 Co-occurrence-Analyse
Häufig kann ein einzelnes Wort je nach Kontext unterschiedliche Bedeutungen annehmen, was ganz verschiedene Informationen ermöglicht.
Der Begriff “Design” ist von entscheidender Bedeutung, wenn es darum geht, das Innovationsmanagement auf struktureller Ebene zu beschreiben (Heyden, Sidhu & Volberda, 2018). Trotz der Verwendung des Begriffs “Design” in den beiden folgenden Phrasen, unterscheiden sie sich grundlegend in ihrer Semantik (Bedeutung).
“Das kontinuierliche Anpassen und Weiterentwickeln des Designs ist entscheidend, um den sich wandelnden Anforderungen und Trends gerecht zu werden.”
“Das bewährte Design der Führungsstruktur sorgt für Stabilität und klare Kommunikationswege innerhalb des Unternehmens.”
Das gemeinsame Auftreten bestimmter Wörter ermöglicht eine Kontextualisierung und Annäherung an die intendierte Bedeutung. Diese Methoden bilden auch die Grundlage für fortgeschrittene Sprachmodelle wie Topic Models und Large Language Models.
Heyden et al. (2018) verwenden diesen Ansatz in einer textbasierten Messung für “Management Innovation” (MI). MI wird definiert als die Einführung von Veränderungen in Managementstrukturen, -prozessen und -praktiken, um die organisatorische Funktionsweise zu verbessern. In dieser Messung werden Wörter aus drei Wörterbüchern (Strukturen; Prozesse; Praktiken) nur dann einzeln gezählt, wenn sie mit Schlüsselwörtern aus einem Wörterbuch für “Change” relevanten Begriffen auftreten.
Um beispielsweise Veränderungen in Strukturen zu messen, wird das Schlüsselwort “design” nur dann als relevant gezählt, wenn sich im Textkontext plus/minus 10 Wörter ein “Change”-relevantes Schlüsselwort findet. In diesem Beispiel sind es gleich drei Treffer: “Anpassen”, “Weiterentwickeln” und “Wandel”.
“Das kontinuierliche Anpassen und Weiterentwickeln des Designs ist entscheidend, um den sich wandelnden Anforderungen und Trends gerecht zu werden.”
“Das bewährte Design der Führungsstruktur sorgt für Stabilität und klare Kommunikationswege innerhalb des Unternehmens.”
Im Folgenden wird solch eine Textanalyse mit den Beschreibungen aus den 32 Coworking-Spaces gezeigt. Es werden die Struktur- und Veränderungsrelevanten Schlüsselworte von Heyden et al. (2018) verwendet. Darüber hinaus wird eine Liste von Schlüsselworten für “Amorphie” einbezogen. Amorphie bezeichnet einen Zustand oder eine Eigenschaft, die durch das Fehlen einer klaren oder geordneten Struktur charakterisiert wird. Im Kontext von MI können damit kategoriale Abiguität, Flexibilität und Fluidität einhergehen.
Hierfür werden zunächst die Beschreibungen der Coworking-Spaces, die als einzelne Text-Datein (.txt) in einem Verzeichnis vorliegen bereinigt. Dabei werden z.B. doppelte Leerzeichen, Satzzeichen, Zahlen und Formatierungen entfernt und der Text wird in Kleinbuchstaben umgewandelt. Mit der Funktion “zaehle_wortliste” werden die Treffer für jedes Wörterbuch gezählt. Die anschließende Funktion “zaehle_co_occurrence” zählt die Treffer für das gemeinsame Auftreten von Schlüsselworten aus zwei Wörterbüchern.
library(tm) # Für das Entfernen von Stopwords
# keywords from Heyden (2018)
structures = c("architect","design","diversif","flex","hierarch","layer","network","outsourc","portfolio","struct")
change = c("adopt","chang","first","implement","improv","innov","modif","new","novel","replac","simplif","strateg","transform","unprecedent")
# keywords from Bouncken_Ratzmann (2024)
amorphous =c("emerg", "fluid", "liquid", "change", "transform", "dynamic", "unfold", "flow", "fluent", "flexib", "adjust", "fluct", "versatil", "modifi")
# Funktion zur Überprüfung, ob eine Datei bereits in der Ergebnis-CSV vorhanden ist
ist_bereits_verarbeitet <- function(dateiname, csv_dateipfad) {
if (file.exists(csv_dateipfad)) {
df <- read.csv(csv_dateipfad, stringsAsFactors = FALSE)
return(dateiname %in% df$Filename)
}
return(FALSE)
}
# Funktion zum Zählen der Wörter in einer Textdatei
clean_text <- function(text) {
# Entferne unvollständige Zeilen
text <- gsub("[\r\n]+$", "", text)
# Entferne Satzzeichen, Zahlen und doppelte Leerzeichen
text <- gsub("[[:punct:]0-9]", "", text)
text <- gsub("\\s+", " ", text)
# Entferne führende und abschließende Leerzeichen
text <- trimws(text)
# Wandle in Kleinbuchstaben um
text <- tolower(text)
return(text)
}
zaehle_wortliste <- function(text, wortliste) {
summe <- 0
for (wort in wortliste) {
x <- nchar(wort)
woerter_text <- unlist(strsplit(text, "\\s+"))
for (wort_text in woerter_text) {
if (nchar(wort_text) >= x) {
if (substr(wort_text, 1, x) == wort) {
summe <- summe + 1
}
}
}
# Suche nach Treffern
}
return(summe)
}
# Funktion zum Zählen der Co-Occurrence zwischen Wörtern aus Liste 1 und Liste 2
zaehle_co_occurrence <- function(text, woerter_liste1, woerter_liste2) {
co_occurrence <- 0
woerter_text <- unlist(strsplit(text, "\\s+"))
i=1
j=1
j_beginn=1
j_end=1
l=1
m=1
# Suche das i-te wort aus Liste 1
for (i in 1:length(woerter_liste1)) {
# verwende das j-te wort aus dem Text
for (j in 1:length(woerter_text)) {
# wenn das i-te Wort aus der Liste gleich dem j-ten Wort des Textes (reduzierte auf die Anzahl der Buchstaben des i-ten Wortes)
if (woerter_liste1[i] == substr(woerter_text[j], 1, nchar(woerter_liste1[i]))) {
#print (paste("HIT in Textposition", j))
#print (paste("Vergleiche ",
# substr(woerter_text[j], 1, nchar(woerter_liste1[i])),
# " & ",
# woerter_liste1[i]))
# Bestimme den Bereich um das j-te Wort des Textes
j_beginn = j-10
j_end = j+10
j_beginn <- ifelse (j_beginn < 1,1,j_beginn)
j_end <- ifelse (j_end < length(woerter_text),j_end, length(woerter_text))
#print (paste("Textbereich:",j_beginn, " - ", j_end))
# Suche im Bereich l
for (l in j_beginn:j_end) {
# und vergleiche das Wort in Position l
# mit dem m-ten Worten in Liste 2
for (m in 1:length(woerter_liste2)) {
# wenn das Wort in Position l des Textes (reduziert auf die Anzahl der Zeichen des m-ten Wortes aus Liste 2) mit dem m-ten Wort der Liste 2 übereinstimmt
co_occurrence <- ifelse (substr(woerter_text[l], 1, nchar(woerter_liste2[m])) == woerter_liste2[m] , co_occurrence+1, co_occurrence)
}
}
}
}
}
return(co_occurrence)
}Im Folgenden werden diese Funktionen für die einzelnen Wörterbücher und ihre Kombinationen aufgerufen und die Ergebnisse in einer Datei abgespeichert.
# Setze den Pfad zum Hauptordner, der die TXT-Dateien enthält
hauptordner_pfad <- "data/cws"
# Setze den Dateipfad für die Ergebnis-CSV Datei
csv_dateipfad <- file.path(hauptordner_pfad, "Results.csv")
# Überprüfe, ob die Ergebnis-CSV vorhanden ist. Wenn nicht, erstelle sie.
if (!file.exists(csv_dateipfad)) {
write.csv(data.frame(Filename = character(), TotalWords = numeric(), Structures = numeric(), Change = numeric(), Amorphous = numeric(), Change_Structures = numeric(), Amorph_Structures = numeric(), Amorph_Change = numeric()),csv_dateipfad, row.names = FALSE)
}
# Liste alle TXT-Dateien im Hauptordner auf
txt_dateien <- list.files(path = hauptordner_pfad, pattern = "\\.txt$", full.names = TRUE)
# Lade und verarbeite jede TXT-Datei
options(warn = -1) # Unterdrücke alle Warnungen
for (datei_pfad in txt_dateien) {
dateiname <- basename(datei_pfad)
if (!ist_bereits_verarbeitet(dateiname, csv_dateipfad)) {
# Lade den Text aus der Datei
text <- paste(readLines(datei_pfad), collapse = " ")
# Bereinige den Text und zähle die Wörter
text <- clean_text(text)
total <- length(unlist(strsplit(text, "\\s+")))
# woerter <- wort_info$Worte
# Zähle die Wörter aus Liste 1 und Liste 2
counts1 <- zaehle_wortliste(text, structures)
counts2 <- zaehle_wortliste(text, change)
counts3 <- zaehle_wortliste(text, amorphous)
# Zähle die Co-Occurrence zwischen den Wörtern aus Liste 1 und Liste 2
co_occur_change_MI_structures <- zaehle_co_occurrence(text, structures, change)
co_occur_amorph_MI_structures <- zaehle_co_occurrence(text, structures, amorphous)
co_occur_amorph_change <- zaehle_co_occurrence(text, change, amorphous)
# Speichere die Ergebnisse in der Ergebnis-CSV
ergebnis <- data.frame(Filename = dateiname, TotalWords = total, Structures = counts1, Change = counts2, Amorphous=counts3, Change_Structures = co_occur_change_MI_structures, Amorph_Structures=co_occur_amorph_MI_structures, Amorph_Change=co_occur_amorph_change)
write.table(ergebnis, csv_dateipfad, sep = ",", col.names = !file.exists(csv_dateipfad), append = TRUE, row.names = FALSE)
}
}
options(warn = 0) # Stelle die Warnungen wieder auf den Standardwert zurückDas Ergebnis der Co-Occurency-Analyse liegt nun in der Datei “result.csv” vor und wird zur weiteren Analyse geladen.
cooccur <- read.csv("data/cws/Results.csv")
questionair <- read.csv("data/cws/CWS_admin_user.csv")
questionair <- questionair[-3]
total <- merge(cooccur, questionair, by = c ("Filename"), all=TRUE)
total <- total[-9:-11]
total <- total[-1]
# Bestimmen der relativen Werte an der Textlänge
total$Structures = total$Structures*100/total$TotalWords
total$Change = total$Change*100/total$TotalWords
total$Amorphous = total$Amorphous*100/total$TotalWords
total$Change_Structures = total$Change_Structures*100/total$TotalWords
total$Amorph_Structures = total$Amorph_Structures*100/total$TotalWords
total$Amorph_Change = total$Amorph_Change*100/total$TotalWords
total <- total[-1]
total <- total[-7:-13]7.2 Verteilungen und Anpassungen
Die Verteilung der Daten in der Stichprobe und innerhalb der Antwortkategorien von Daten hat einige zentrale Aspekte für die Anwendbarkeit von spezifischen Methoden, wie z.B. der Regression. Daher werden hier einige mögliche bzw. typische Verteilungsformen dargestellt.
Das folgende Skript zeigt die Anpassung aller Variablen eines Datensets an die Normalverteilung. Dazu wird hier das R-Package “bestNormalize” eingesetzt werden, welches eine Vielzahl von möglichen Transformationen prüft und automatisiert auf die spezifische Verteilung anwendet.
## Loading required package: bestNormalize##
## Attaching package: 'bestNormalize'## The following object is masked from 'package:MASS':
##
## boxcoxlibrary(bestNormalize)
#data_norm <- function(df) {
# par(mfrow=c(2,2))
# for (i in 1:ncol(df)) {
# hist(df[,i], xlab=colnames(df[i]), main="Histogram")
# boxplot(df[,i], main=colnames(df[i]))
# x_bN <- bestNormalize(df[,i] , allow_lambert_s = TRUE)
# #Transformation anwenden
# df[,i] <- predict (x_bN)
# hist(df[,i], xlab=colnames(df[i]), main="Histogram")
# boxplot(df[,i], main=colnames(df[i]))
# Sys.sleep(1)
# }
#return(df)
#}
#total <- data_norm (total)Am Beispiel der Häufigkeit von “Change”-relevanten Worten (Heyden et al., 2018) werden hier Häufigkeitsdiagramm und Box-Plot gezeigt.
x_bN <- bestNormalize(total$Change , allow_lambert_s = TRUE)
total$Change_norm <- predict (x_bN)
par(mfrow=c(2,2))
hist(total$Change, xlab="Change (rel.Anteil)", main="Histogram")
hist(total$Change_norm, xlab="Change (Normalisiert)", main="Histogram")
boxplot(total$Change, main="Change (rel.Anteil)")
boxplot(total$Change_norm, main="Change (normalisiert)")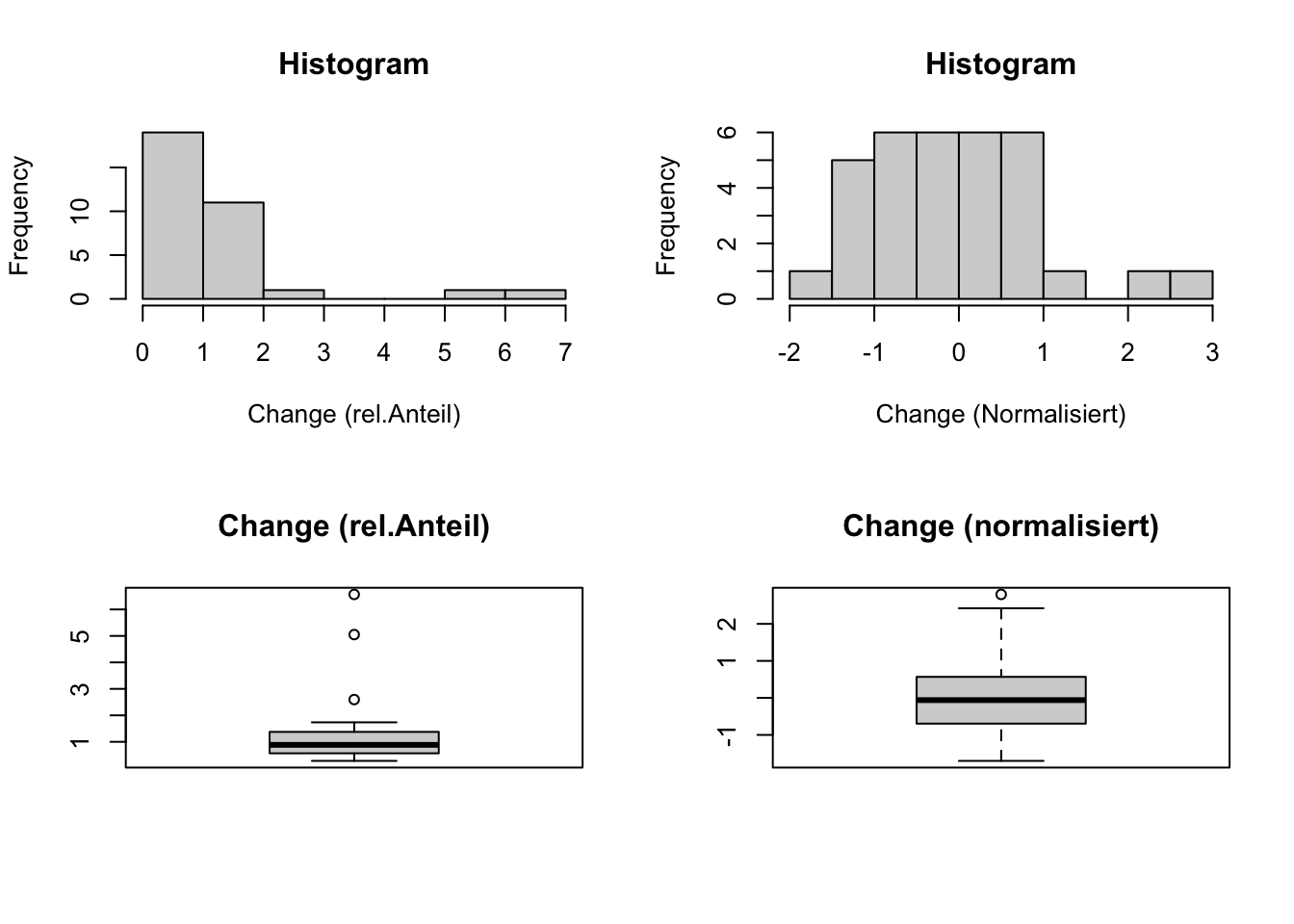
Das Histogramm weist nach der Transformation eine deutliche Annäherung (Approximation) an die Normalverteilung auf.
7.2.1 Ausreißer
Im folgenden ist eine relativ unkomplizierte Vorgehensweise dargestellt, um Ausreißer zu erkennen und zu bereinigen. Hierbei betrachte ich als Ausreißer alle Werte, die mehr als das Doppelte der Standardabweichung vom Mittelwert der Stichprobe abweichen. Diese Ausreißer werden im Anschluss auf diesen Wert begrenzt.
#data_fit <- function(df) {
# for (i in 1:ncol(df)) {
# df[,i] <- ifelse(is.na(df[,i]) == "TRUE", 0, df[,i])
# par(mfrow=c(2,2))
# hist(df[,i], xlab=colnames(df[i]), main="Histogram")
# boxplot(df[,i], main=colnames(df[i]))
# m=mean(df[,i], na.rm=TRUE)
# s=sd(df[,i], na.rm=TRUE)
# df[,i] <- ifelse (df[,i] > m + 2*s, m+ 2*s, df[,i])
# df[,i] <- ifelse (df[,i] < m - 2*s, m- 2*s, df[,i])
# boxplot(df[,i], main=colnames(df[i]))
#cata[,i] <- scale(cata[,i])
# Sys.sleep(1)
# }
#return(df)
#}
#total <- data_fit (total)Hier wird nur die Variable “Change” geprüft und angepasst.
m=mean(total$Change, na.rm=TRUE)
s=sd(total$Change, na.rm=TRUE)
total$Change_bereinigt <- ifelse (total$Change > m + 2*s, m+ 2*s, total$Change)
total$Change_bereinigt <- ifelse (total$Change < m - 2*s, m- 2*s, total$Change)
total_change = total[,c("Change", "Change_norm", "Change_bereinigt")]
total_change <- total_change[complete.cases(total_change),]
par(mfrow=c(1,2))
boxplot(total_change$Change, main="Change (rel. Häufigkeit)")
boxplot(total_change$Change_bereinigt, main="Change (ausreißerbereinigt)")
7.2.2 Logistische Transformation
Wird eine fünfstufige Ratingskala (mit Werten von 1 bis 5) in die logistische Funktion transformiert, resultiert die Wahrscheinlichkeitsfunktion, welche die Wahrscheinlichkeit für die Zustimmung in Abhängigkeit von der Intensität der Zustimmung widerspiegelt. Die transformierten Werten weisen dann einen Wertebereich von 0 bis 1 auf.
Die theoretische Wahrscheinlichkeitsfunktion \(f(x)=\frac{1}{1+exp(-x)}\) resultiert dann unter Berücksichtigung des Median (als Erwartungswert \(\alpha\)) und Varianz der Werte (als Steilheit \(\beta\) der Verteilung) in der empirischen Wahrscheinlichkeitsfunktion für X=1:
\[p(X=1)=f(x)=\frac {1}{1+e^{-\frac{x-\alpha}{\beta}}}\]
wobei:
\[ \beta = \sqrt {\frac{var(x)*3}{\pi^2}}\]
Die Eulersche Zahl entspricht der Exponentialfunktion von 1 (\(e = exp(1)\)), so dass \(e^x = exp(x)\) und \(e^{-x} = exp(-x)\).
Im Beispiel wird die logistische Verteilung der Wortzählungen von “Change” erstellt. Im Anschluss werden die bi-variaten Korrelationen der vier Variablen (Rohwert, normalisiert, bereinigt, logistisch) bestimmt.
alpha = median(total_change$Change)
beta = sqrt(var(total_change$Change)*3/pi^2)
total_change$Change_p = 1/(1+exp(-((total_change$Change-alpha)/beta)))
par(mfrow=c(1,2))
hist(total_change$Change_p, main="Histogramm", xlab="p(Change)")
boxplot(total_change$Change_p, main="p (Change)")
## Change Change_norm Change_bereinigt Change_p
## Change 1.00 0.89 1.00 0.86
## Change_norm 0.89 1.00 0.89 0.98
## Change_bereinigt 1.00 0.89 1.00 0.86
## Change_p 0.86 0.98 0.86 1.007.2.3 Logarithmische Transformation
Skalen die keine obere Begrenzung aufweisen, haben keinen maximalen Wert. So kann beispielweise die Anzahl der Mitarbeiter (abgesehen von der Bevölkerung bzw. der räumlichen Grenzen des Systems) theoretisch bis ins Unendliche reichen.
Daten die exponentielles Ausmaß aufzeigen, können durch eine logarithmische Transformation linearisiert werden, was die Analyse und Modellierung erleichtert.
Die logarithmische Transformation wendet den natürlichen Logarithmus (oder einen anderen Logarithmus, wie den Basis-10-Logarithmus) auf jede Beobachtung in einem Datensatz an. Wenn \(x\) der ursprüngliche Wert ist, wird er transformiert zu \(log(x)\).
7.2.4 Lineare Skalentransformation
Skalen unterschiedlicher Länge können durch eine einfache lineare Transformation auf ein einheitliches Maß transformiert. Entscheidend dafür der Bereich der Skala, der im folgenden Beispiel von 1 bis 5 reicht und auf einen Wertebereich von 0 bis 1 transformiert werden soll.
7.3 Äquivalenz-Ratio
In Kapitel 6.1 ist Äquivalenz \(X \leftrightarrow Z\) als logische Verknüpfung zweier elementarer Aussagen für den Fall beschrieben, dass X und Z immer den gleichen Wahrheitswert aufweisen. Entweder sind beide falsch (0) oder beide sind wahr (1).
Lässt sich in Daten nur geringe Äquivalenz in den Ausprägungen der unabhängigen und abhängigen Variablen aufzeigen, kann die unabhängige Variable die Varianz der abhängigen Variablen möglicherweise nicht ausreichend erklären. Das Regressionsmodell kann dann aus der Berücksichtigung von Interaktionstermen profitieren.
Im Folgenden werden die Daten der Textanalyse der 32 Coworking-Spaces verwendet. Mit dem Dictionairy von Heyden et al. (2018) werden “Structure”-relevante Worte erfasst und mit dem Dictionairy “Amorphous” (Bouncken, Ratzmann, Schmitt & Covin) werden “Amorphie”-bezogene Worte erfasst.
Im ersten Schritt werden die Wortzählungen für beide Konzepte in die empirischen Wahrscheinlichkeitsverteilungen transformiert.
set = total[,c("Change","Amorphous","Structures")]
set = set[complete.cases(set),]
# logistische Transformation
alpha = median(set$Change)
beta = sqrt(var(set$Change)*3/pi^2)
Change_p = 1/(1+exp(-((set$Change-alpha)/beta)))
alpha = median(set$Amorphous)
beta = sqrt(var(set$Amorphous)*3/pi^2)
Amorphous_p = 1/(1+exp(-((set$Amorphous-alpha)/beta)))
alpha = median(set$Structures)
beta = sqrt(var(set$Structures)*3/pi^2)
Structures_p = 1/(1+exp(-((set$Structures-alpha)/beta)))
par(mfrow=c(1,2))
plot(Structures_p,Amorphous_p, xlab="p(Structures)", ylab="p(Amorphous)")
plot(Amorphous_p, Structures_p, xlab="p(Amorphous)", ylab="p(Structures)")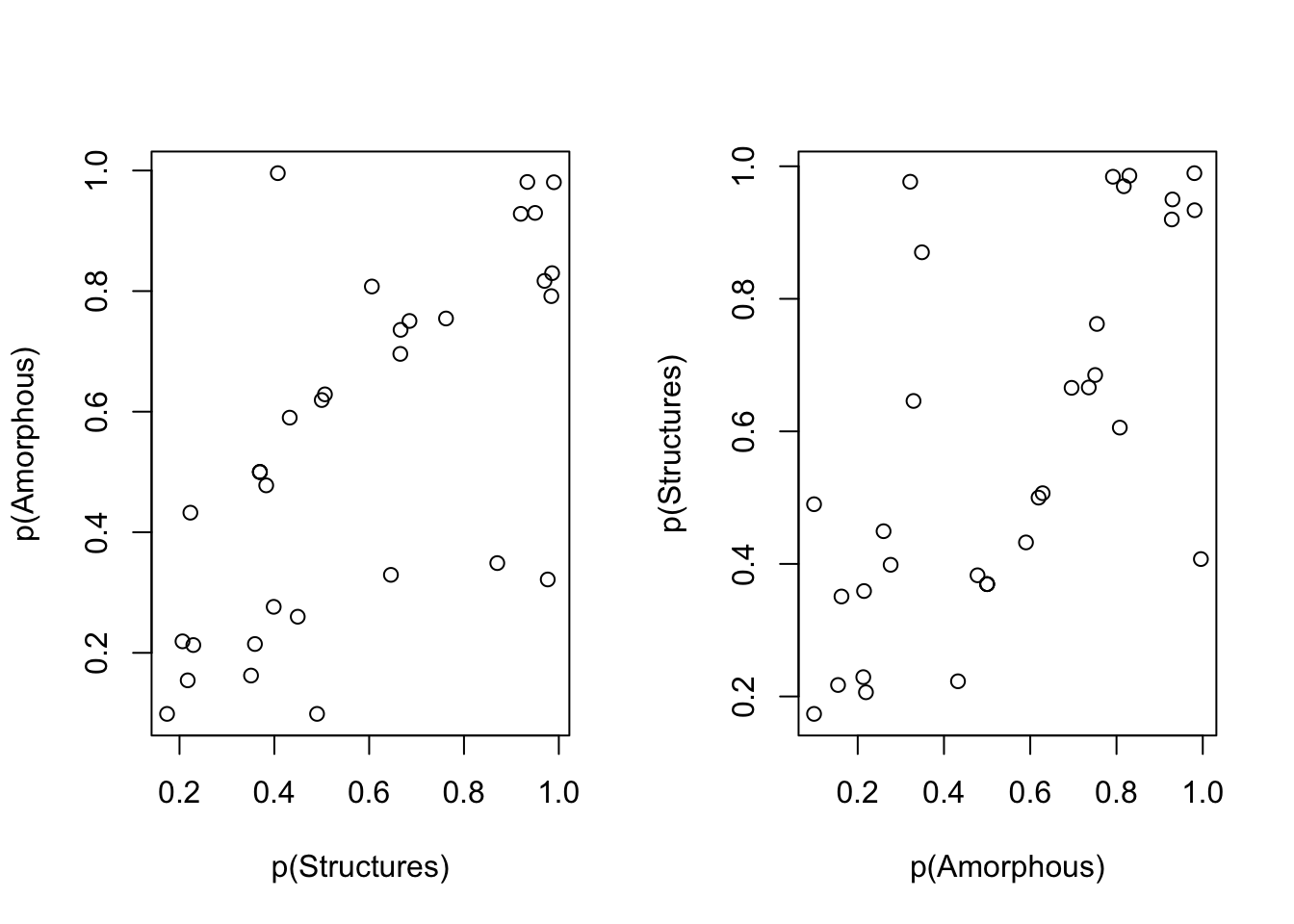
x= Amorphous_p
z = Structures_p
equivalencebound=0.05
eblow = z-(0.5*equivalencebound)
ebhigh= z+(0.5*equivalencebound)
e = ifelse (x>eblow & x<ebhigh,1,0)
s = ifelse (x < eblow,1,0)
n = ifelse (x > ebhigh ,1,0)
a=sum (e)/ (sum (e)+sum (s)+sum (n))
b=sum (s)/ (sum (e)+sum (s)+sum (n))
c=sum (n)/ (sum (e)+sum (s)+sum (n))
ARatio = round(a/(b+c),3)
NRatio = round(a/b - a/c,3)
test=cbind(x,z,eblow, ebhigh, e,s,n)
par(mfrow=c(1,1))
colors <- ifelse(e == 1, "green", ifelse(s == 1, "blue", ifelse(n == 1, "red", "black")))
# Plot erstellen
plot(x, z, col = colors, pch = 19,
xlim=c(0,1),
ylim=c(0,1),
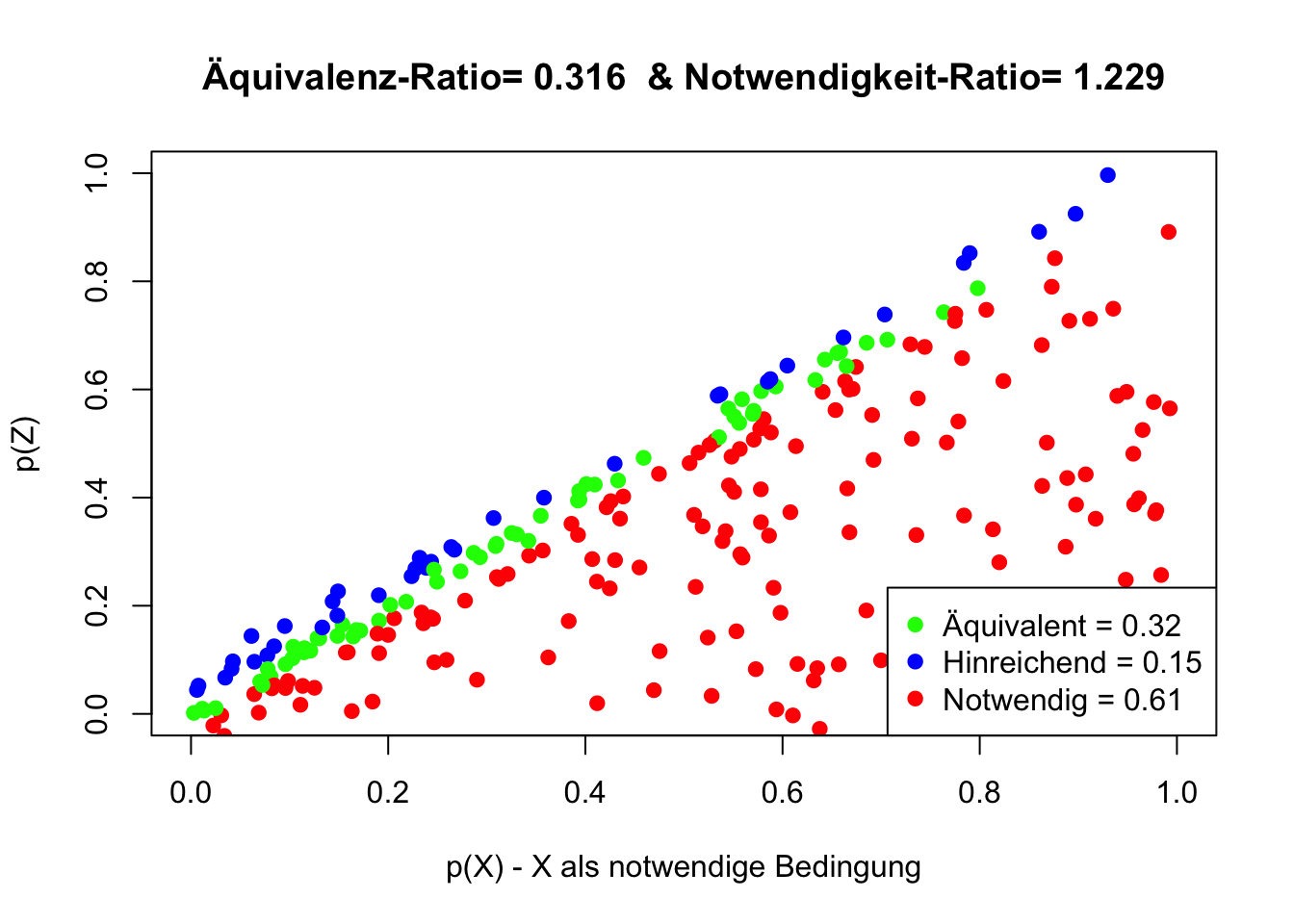
main = paste("Äquivalenz-Ratio=",ARatio, " & Notwendigkeit-Ratio=",NRatio),
xlab = "p(Amorphous)",
ylab = "p(Structures)")
# Hinzufügen einer Legende
legend("bottomright", legend = c(paste("Äquivalent =",round((sum(e)/(sum(s)+sum(n))),2)), paste("Hinreichend =",round((sum(s)/(sum(e)+sum(s)+sum(n))),2)), paste("Notwendig =",round((sum(n)/(sum(e)+sum(s)+sum(n))),2))),
col = c("green", "blue", "red"), pch = 19)
Die Abbildung zeigt Fälle, in denen “Amorphous” und “Structures” als Äquivalent auftreten (grün markiert). Mit einer Auftretens-Wahrscheinlichkeit von \(p(Äquivalenz)=0.22\), wird Äquivalenz deutlich seltener aufgezeigt, als die Einordnung von Amorphie als hinreichende (p=0.39) oder notwendige (p=0.42) Bedingung für Struktur.
Die Äquivalenz-Ratio < 1 weist eine Äquivalenz von Amorphie und Strukturen zurück. Das positive Vorzeichen der Notwendigkeits-Ratio indiziert Notwendigkeit, der geringe Betrag widerspricht jedoch einer klaren Aussage. Der absolute Betrag der Notwendigkeits-Ratio sollte wenigsten 0.2 überschreiten.
Entsprechend der Definition: Amorphie bezeichnet einen Zustand oder eine Eigenschaft, die durch das Fehlen einer klaren oder geordneten Struktur charakterisiert wird. sollten “Structures” und “Amorphous” einander ausschließen, also Kontravalenz aufzeigen.
Um dies weiter zu untersuchen, bestimmen wir zunächst die Gegenwahrscheinlichkeit von Amorphie: \[1 - p(Amorphie)\]
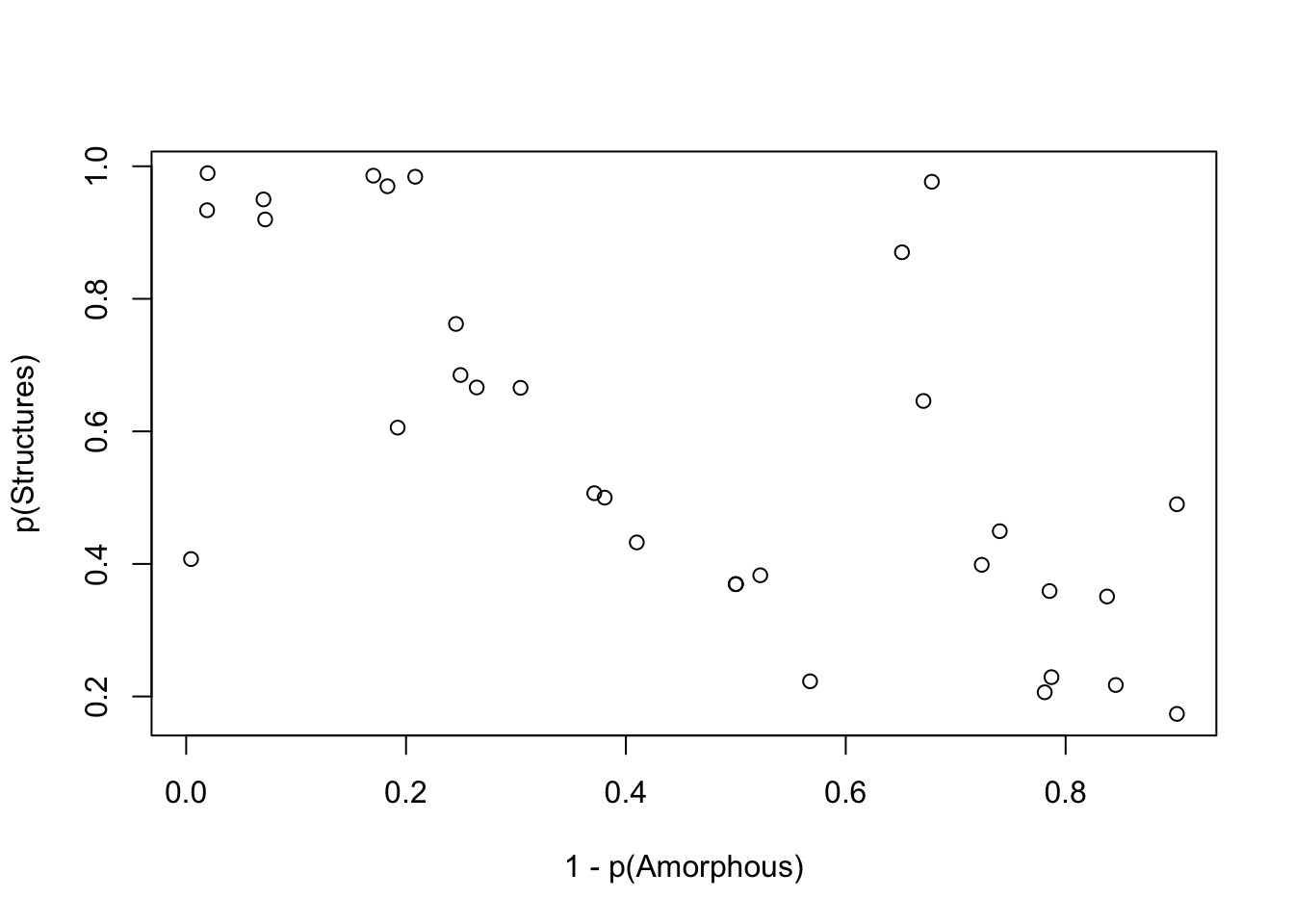
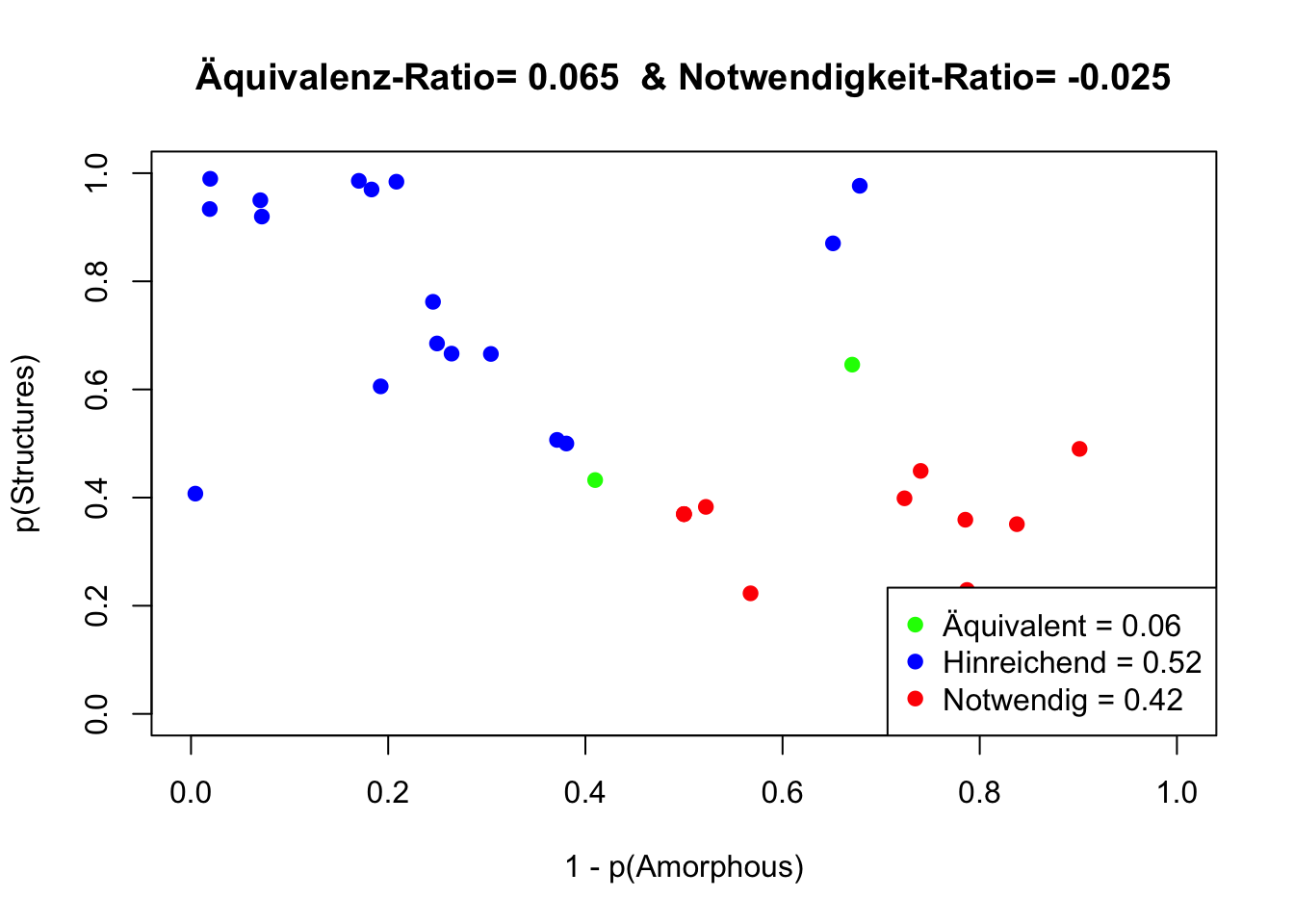
Die Abwesenheit von Amorphie, welche laut Definition “das Fehlen einer klaren oder geordneten Struktur charakterisiert”, sollte eine notwendige Bedingung für Struktur sein. Um Struktur zu haben, dürfte Amorphie nicht vorhanden sein. Daher wäre die Abwesenheit von Amorphie notwendig für Struktur.
Die Abbildung zeigt weitere Hinweise zur begrifflichen Abgrenzung dieser Konzepte. Die Abwesenheit von Amorphie stellt sich weder als notwendige noch als hinreichende Bedingung für Struktur dar. Struktur tritt auch ohne das Fehlen von Amorphie auf. Das Fehlen von Amorphie führt nicht immer zu Struktur.
Aufgrund der geringen Notwendigkeits-Ratio wird nahegelegt, dass es sich hier weniger um eine Darstellung von Ursache-Wirkungs-Beziehungen (Kausalität) handelt, als vielmehr um eine Debatte konkurrierender Sichtweisen (Dialektik).
Die folgende Abbildung ist in Kapitel 6.1.3 als charakteristische Darstellung einer hinreichenden Bedingung im Streudiagramm aufgeführt.
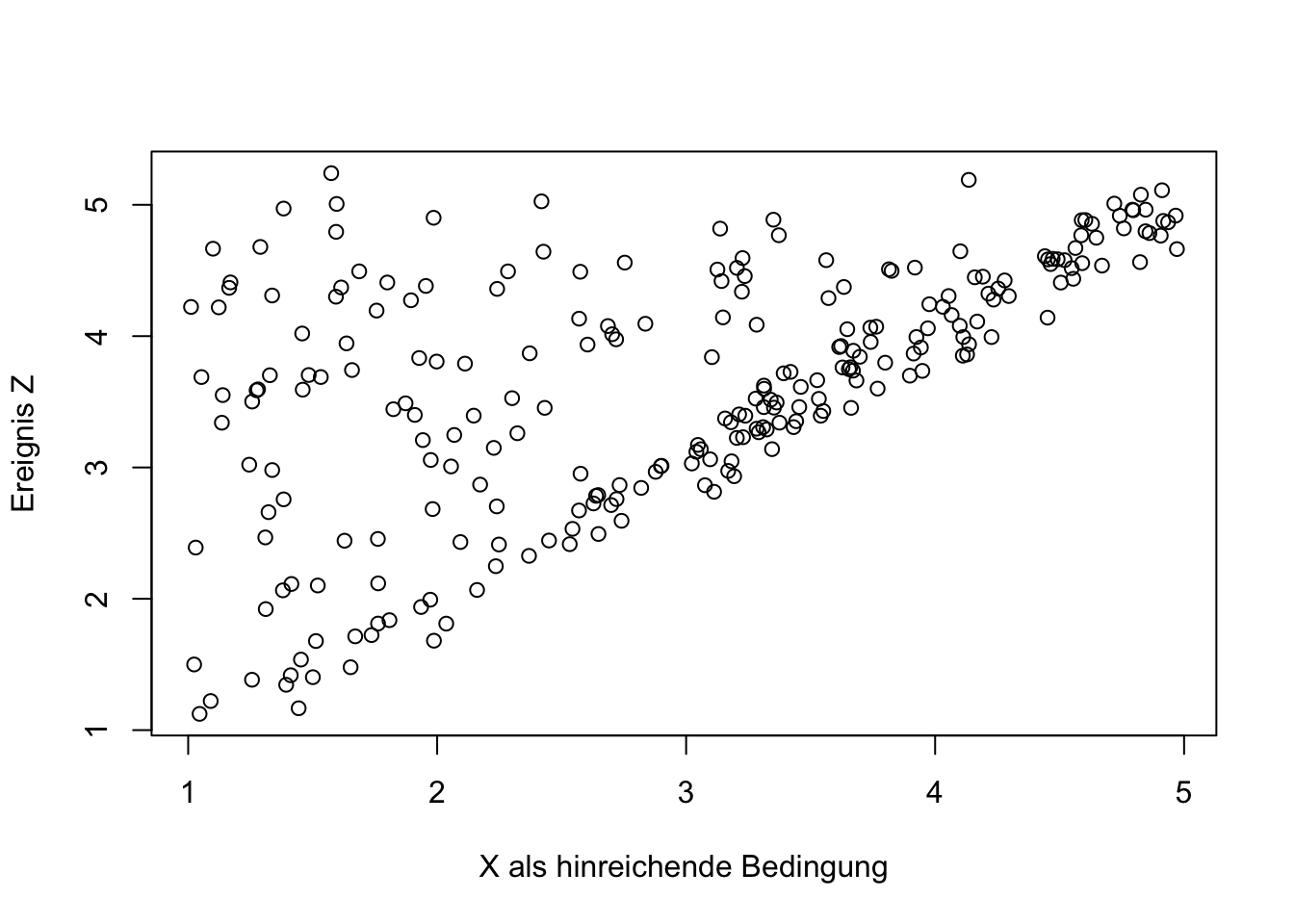
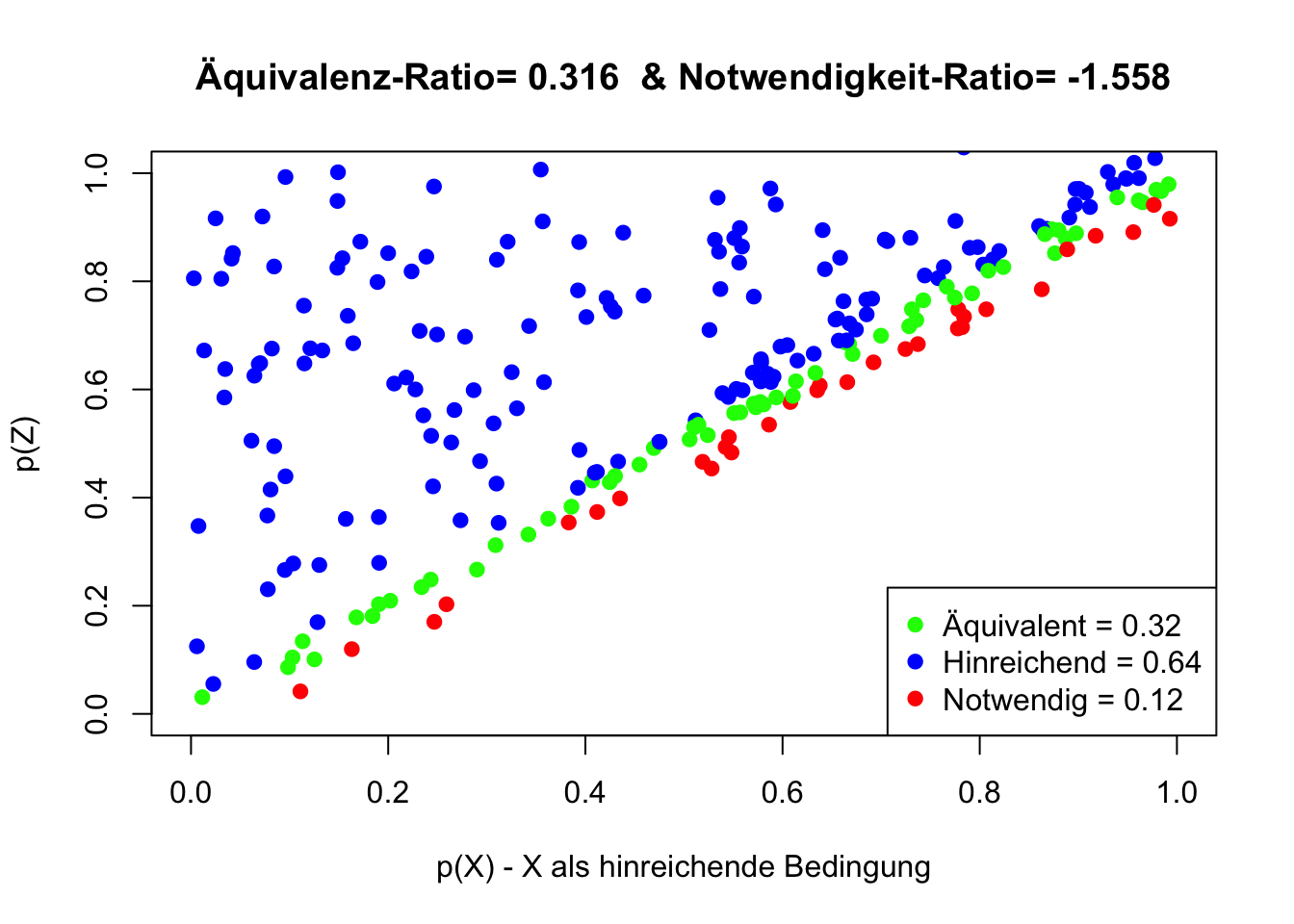
Die Äquivalenz-Ratio ist kleiner als 1 und widerspricht der Äquivalenz-Annahme. Der Betrag der Notwendigkeits-Ratio ist deutlich größer als 0.2, das Vorzeichen ist jedoch negativ. Dies widerspricht der Notwendigkeits-Annahme.
Die folgende Abbildung ist in Kapitel 6.1.4 als charakteristische Darstellung einer notwendigen Bedingung im Streudiagramm aufgeführt.
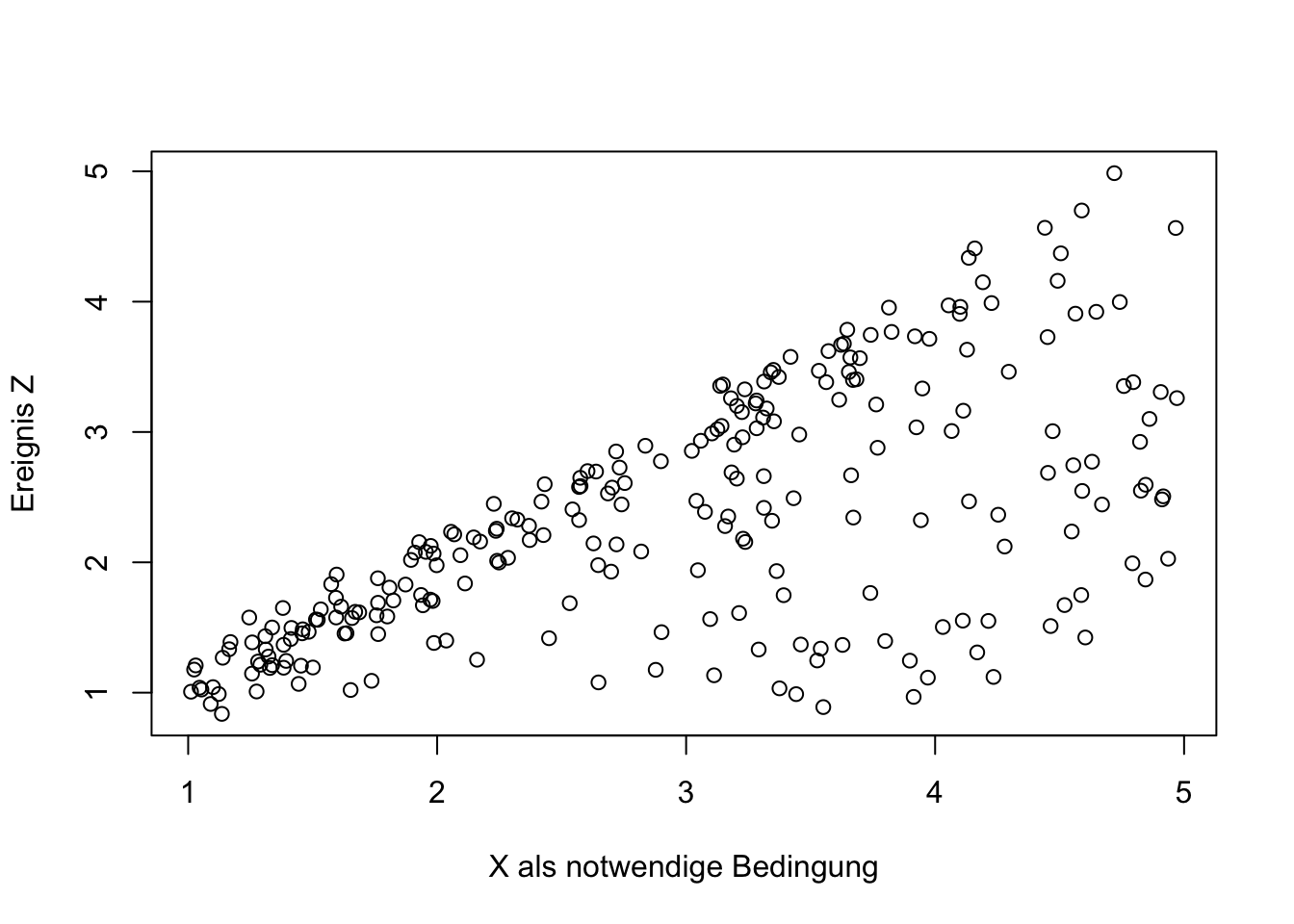
Die Äquivalenz-Ratio ist kleiner als 1 und widerspricht der Äquivalenz-Annahme. Der Betrag der Notwendigkeits-Ratio ist deutlich größer als 0.2, das Vorzeichen ist positiv und dies unterstützt die Notwendigkeits-Annahme.
7.4 Parallel Analysis
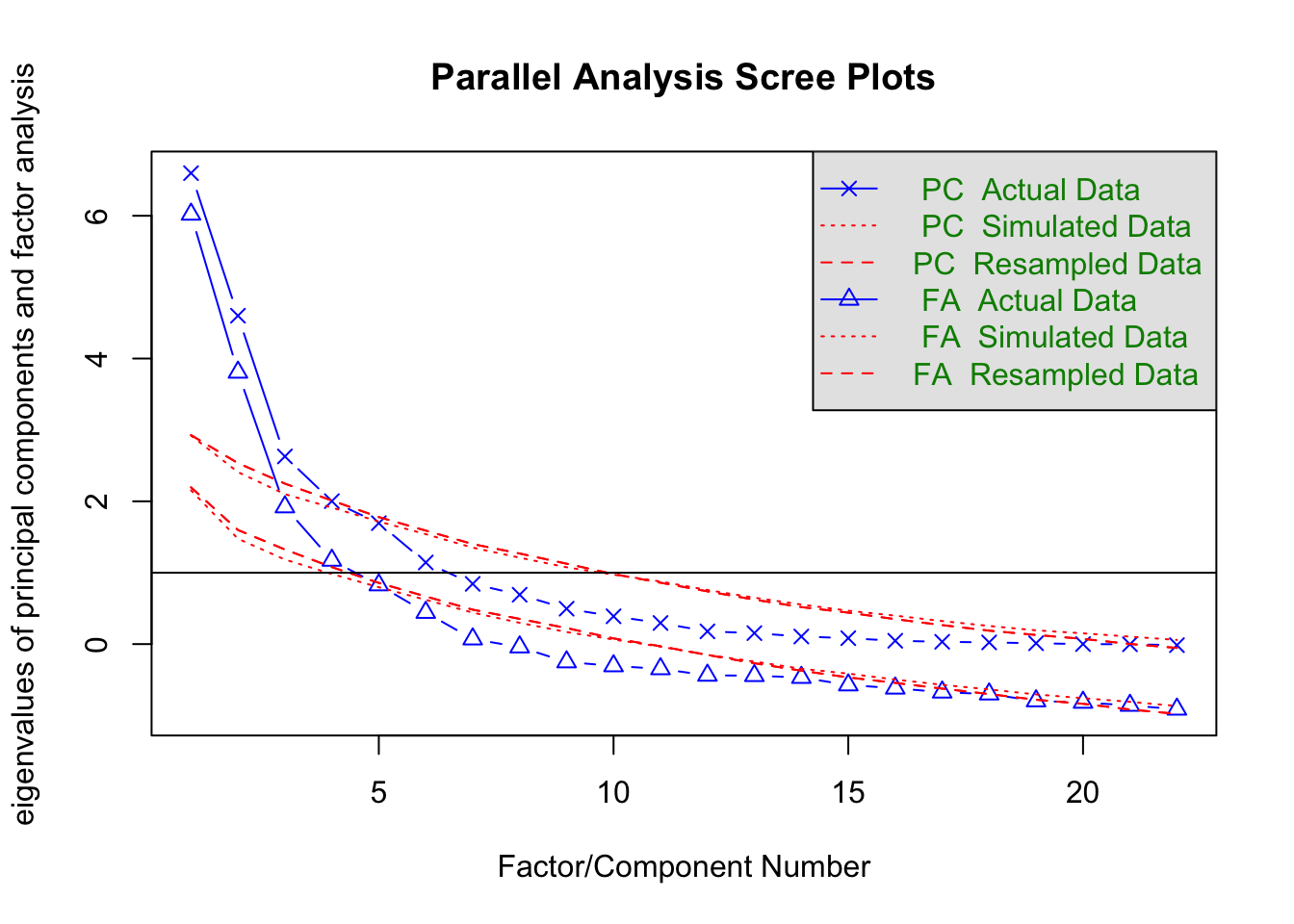
## Parallel analysis suggests that the number of factors = 4 and the number of components = 4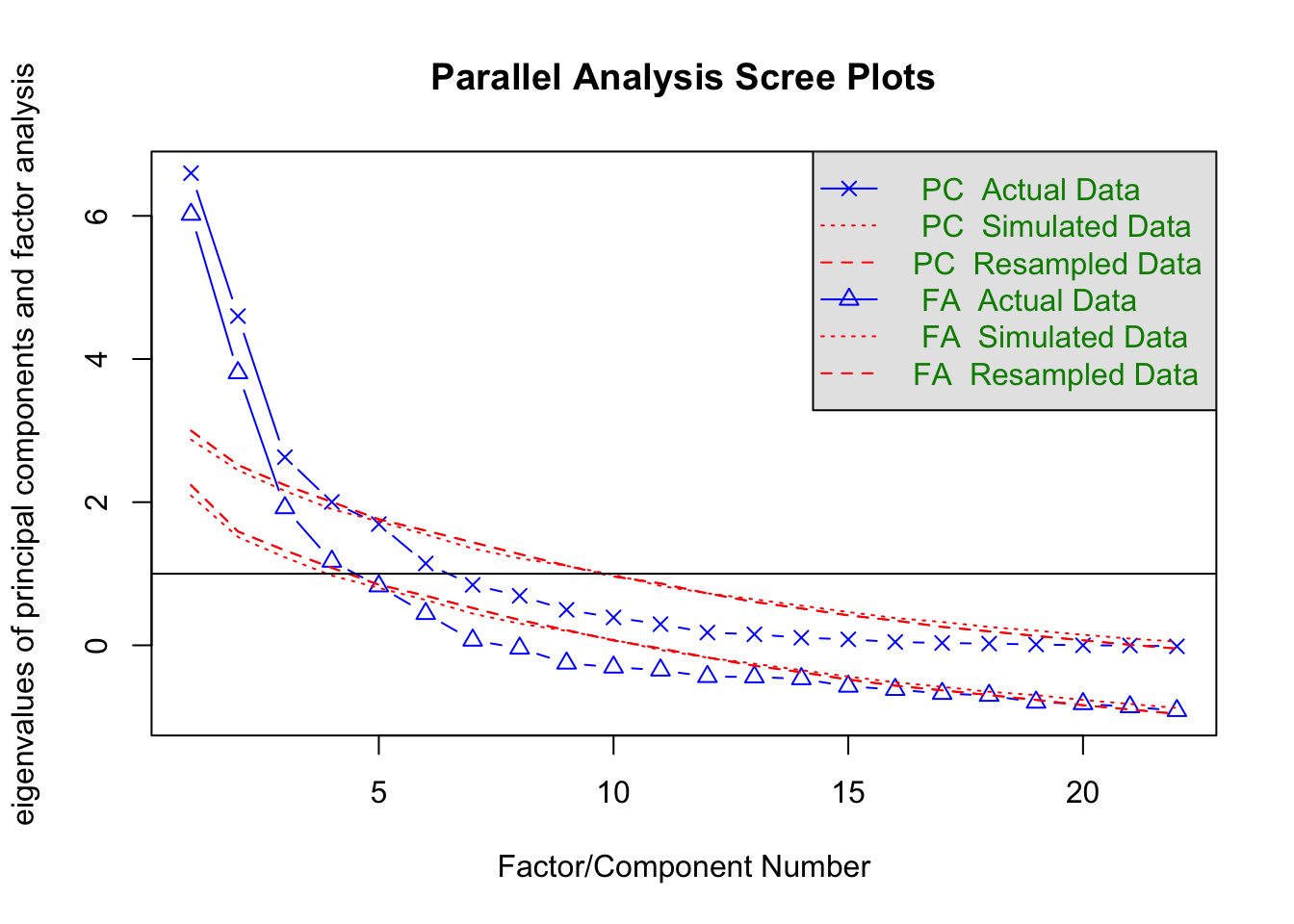
## Parallel analysis suggests that the number of factors = 4 and the number of components = 3## [1] 6.02071983 3.80724679 1.92080023 1.17294420 0.82852085 0.44264606
## [7] 0.07045691 -0.04123880 -0.25038655 -0.30575076 -0.34698177 -0.43762001
## [13] -0.44234459 -0.46825272 -0.57323528 -0.61807020 -0.67362957 -0.70031195
## [19] -0.79619364 -0.81656702 -0.85922784 -0.91280413## [1] 2.09194630 1.51317690 1.22893996 0.97419181 0.80166103 0.63406886
## [7] 0.44283237 0.30341956 0.20203012 0.07747194 -0.06474955 -0.17155245
## [13] -0.25739380 -0.34738845 -0.43696453 -0.51641269 -0.58050468 -0.64927190
## [19] -0.69548048 -0.76330823 -0.81942969 -0.87533534## [1] 6.596760e+00 4.599934e+00 2.628680e+00 2.002459e+00 1.694172e+00
## [6] 1.143292e+00 8.439827e-01 6.915360e-01 4.961236e-01 3.893476e-01
## [11] 2.954710e-01 1.783237e-01 1.534847e-01 1.064193e-01 8.278016e-02
## [16] 4.673799e-02 3.238122e-02 2.356195e-02 1.176427e-02 4.508113e-16
## [21] -2.441274e-03 -1.477090e-02## [1] 2.87335571 2.44664614 2.15705966 1.90151778 1.73059563 1.54834674
## [7] 1.35217294 1.21504956 1.11059708 0.98490753 0.83097654 0.72678974
## [13] 0.64216582 0.55430029 0.46456569 0.38112859 0.32583271 0.25682277
## [19] 0.20426882 0.14753312 0.09346474 0.05190241## Factor Analysis using method = minres
## Call: fa(r = HTMT, nfactors = 3, rotate = "promax", fm = "minres")
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR2 MR3 h2 u2 com
## Structures -0.87 0.15 -0.03 0.86 0.13747 1.1
## Change 0.23 0.88 0.08 0.75 0.24676 1.2
## Amorphous -0.71 0.37 0.02 0.78 0.21696 1.5
## Change_Structures 0.02 0.93 -0.07 0.84 0.16259 1.0
## Amorph_Structures -0.97 -0.23 0.08 0.84 0.16336 1.1
## Amorph_Change 0.02 1.00 -0.05 0.98 0.02467 1.0
## WS_E1 0.00 -0.12 0.99 0.94 0.05984 1.0
## WS_E2 0.11 -0.10 0.95 0.95 0.05323 1.0
## WS_E3 0.92 0.00 0.10 0.91 0.08967 1.0
## WS_E4 0.23 -0.78 0.24 0.77 0.22905 1.4
## WS_E5 0.80 -0.32 -0.13 0.85 0.14822 1.4
## WS_E6 0.43 -0.77 0.27 1.00 -0.00061 1.8
## WS_E7 1.00 0.18 0.09 1.00 -0.00064 1.1
## Team_E1 -0.09 0.02 0.96 0.89 0.10699 1.0
## Team_E2 -0.02 0.01 0.98 0.96 0.03703 1.0
## Team_E3 0.77 0.15 0.17 0.66 0.33911 1.2
## Team_E4 -0.42 -0.68 -0.08 0.53 0.46749 1.7
## Team_E5 0.93 -0.04 -0.45 0.87 0.12533 1.5
## Team_E6 0.39 -0.45 -0.25 0.50 0.49520 2.6
## Team_E7 0.80 0.19 0.27 0.79 0.20610 1.3
##
## MR1 MR2 MR3
## SS loadings 7.50 4.91 4.28
## Proportion Var 0.37 0.25 0.21
## Cumulative Var 0.37 0.62 0.83
## Proportion Explained 0.45 0.29 0.26
## Cumulative Proportion 0.45 0.74 1.00
##
## With factor correlations of
## MR1 MR2 MR3
## MR1 1.00 -0.28 0.27
## MR2 -0.28 1.00 0.20
## MR3 0.27 0.20 1.00
##
## Mean item complexity = 1.3
## Test of the hypothesis that 3 factors are sufficient.
##
## df null model = 190 with the objective function = 81.41 with Chi Square = 1099.1
## df of the model are 133 and the objective function was 51.58
##
## The root mean square of the residuals (RMSR) is 0.07
## The df corrected root mean square of the residuals is 0.08
##
## The harmonic n.obs is 22 with the empirical chi square 38.26 with prob < 1
## The total n.obs was 22 with Likelihood Chi Square = 593.12 with prob < 2.6e-59
##
## Tucker Lewis Index of factoring reliability = 0.119
## RMSEA index = 0.394 and the 90 % confidence intervals are 0.373 0.439
## BIC = 182.01
## Fit based upon off diagonal values = 0.987.5 Übereinstimmungs-Koeffizienten
Übereinstimmungs-Koeffizienten werden verwendet, um die Zuverlässigkeit von Aussagen, Bewertungen oder Ansichten zwischen Bewertern zu bestimmen. Im folgenden werden die Bewertungen von zwei Experten hinsichtlich der Frage dargestellt, welche der aufgeführten Worte bzw. Wortstämme sich eignen, um das Konzept der Amorphie zu beschreiben. Das Konzept wird dafür wie folgt definiert: “Amorphie bezeichnet einen Zustand oder eine Eigenschaft, die durch das Fehlen einer klaren oder geordneten Struktur charakterisiert wird. Damit können kategoriale Abiguität, Flexibilität und Fluidität einhergehen”.
Zustimmung bzw. die Zuordnung der Worte zu dem Konzept durch die Experten sind in der Tabelle mit “1” kodiert. Worte, die von den Experten nicht zugeordnet wurden, weisen in der entsprechenden Zelle den Wert “0” auf.
\[\begin{array}{|c|c|c|c|c|} \hline \ & & & \text{ } & \\ \ & Experte_1 & Experte_2 & \text{keine Übereinstimmung} & \text{Übereinstimmung} \\ \hline \text{emerg} & \text{1} & \text{1} & \text{0} & \text{1} \\ \text{fluid} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{liquid} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{change} & \text{1} & \text{1} & \text{0} & \text{1} \\ \text{transform} & \text{1} & \text{1} & \text{0} & \text{1}\\ \text{dynamic} & \text{1} & \text{0} & \text{1} & \text{0}\\ \text{unfold} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{flow} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{fluent} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{flexib} & \text{0} & \text{1} & \text{1} & \text{0}\\ \text{adjust} & \text{1} & \text{0} & \text{1} & \text{0}\\ \text{fluct} & \text{1} & \text{1} & \text{0} & \text{1}\\ \text{versatil} & \text{0} & \text{1} & \text{1} & \text{0} \\ \text{modifi} & \text{1} & \text{1} & \text{0} & \text{1}\\ \hline \text{Summe:} & \text{14} & \text{14} & \text{9} & \text{5} \\ \hline \end{array}\]
7.5.1 Holsti’s Koeffizient C.R.
Die einfachste Form ist die Bestimmung der übereinstimmenden Urteile als Anteil der übereinstimmenden Urteile an der Anzahl aller Urteile Cohen (1960), wie es z.B. von Holsti (1969) als “coefficient of reliability” vorgeschlagen wurde. the “coefficient of reliability [as] the ratio of coding agreements to the total numer of coding decisions”(Holsti, 1969, S. 140)
\[C.R. = \frac{2M} {N_a + N_b} = \frac {2 \cdot 5} {14+14} = 0.357\] Insbesondere eine Darstellung wie bei Short, Broberg, Cogliser & Brigham (2010, S. 328) ist mit Vorsicht zu betrachten, solang die mathematischen Grundgesetze gelten.
\[PA_O= 2A/n_A + n_B\]
7.5.2 Krippendorff’s alpha
Besser geeignet scheint der Koeffizient von Krippendorff (1987), welcher in seiner allgemeinen Form das Verhältnis der beobachtete zur theoretischen Meinungsverschiedenheit berücksichtigt. :
\[\alpha = 1 - D_e/D_t \] wobei \(D_e\) die empirische beobachtete Meinungsverschiedenheit und \(D_t\) die theoretische Meinungsverschiedenheit darstellt.
Bei nominalen Daten resultiert \(D_0\) aus der Summe der Fälle, in denen die Bewerter nicht in der gleichen Kategorie geantwortet haben (\(D_0=9\)).
In der Kontingenztafel wird aufgezeigt, wie die Häufigkeiten für fehlende und nicht fehlende Übereinstimmung verteilen. Es gibt kein einiziges Wort, dass von beiden Rater übereinstimmend ausgeschlossen wurde (a=0). Fünf der Worte (d=5) wurden von beiden Ratern übereinstimmend eingeschlossen. Übereinstimmung basiert demnach nur in der gemeinsamen Zustimmung jedoch nicht in der gemeinsamen Ablehnung.
Fehlende Übereinstimmung (Meinungsverschiedenheit) findet sich in den neun Fällen, in denen das entsprechende Wort von Rater 1 eingeschlossen und von Rater 2 ausgeschlossen wurde (b=7) und in denen das Wort von Rater 1 ausgeschlossen wurde, aber von Rater 2 eingeschlossen wurde (c=2).
Die beobachtete Meinungsverschiedenheit ergibt sich dann als: \[\begin{array}{|c|c|c|c|c|} \hline \ & 0 & 1 & \text{Summe} \\ \hline \text{0} & \text{ a=0 } & \text{ b=7 } & \text{ 7 } \\ \text{1} & \text{ c=2 } & \text{ d=5 } & \text{ 7 }\\ \hline \text{Summe} & \text{2} & \text{12} & \text{14} \\ \hline \end{array}\]
Die empirischen Wahrscheinlichkeiten entsprechen dann:
\[\begin{array}{|c|c|c|c|c|} \hline \ & 0 & 1 & \text{Summe} \\ \hline \text{0} & \text{ a=0.00 } & \text{ b=0.5 } & p_1= \text{ 0.5 } \\ \text{1} & \text{ c=0.14 } & \text{ d=.36 } & q_1 =\text{ 0.5 }\\ \hline \text{Summe} & p_2=\text{0.14} & q_2=\text{0.86} & \text{1} \\ \hline \end{array}\]
Wenn sich \(p\) ergibt als:
\[ p=\frac{p_1+p_2}{2}=1-q \] resultiert für \(\alpha\):
\[ \alpha = 1- \frac {n+1}{n} \frac {\frac {b+c}{2}}{p q} = 1-\frac {3}{2} \frac {\frac{0.64}{2}}{0.32 \cdot 0.68} = 1-1.5 \cdot \frac{0.32}{0.22} = 1 - 2.18 = -1.18 \]
Um den Krippendorff’s Alpha für die Bewertungen von 15 Bewertern zu berechnen, die jeweils 10 Items mit 0 oder 1 bewerten, können Sie die Funktion kripp.alpha() aus dem Paket irr in R verwenden. Hier ist ein Beispiel, wie Sie das tun können:
Diese gesamte Analyse vergleicht die Antworten von 6 Teilnehmern, die jeweils 22 Items mit 0 oder 1 bewerten, und berechnet dann den Krippendorff’s Alpha für diese Daten.
Zudem wird die Zustimmung für die relevanten Schlüsselworte, für die Schlüsselworte eines ähnlichen Konstruktes (change) und zwei diskriminiertende Schlüsselworte separat bestimmt.
Zusätzlich wird zwischen Teilnehmern unterschieden, die sich ihrer Kompetenz hinsichtlich der Aufgabe eher sicher oder sehr sicher waren und denen, die sich eher oder sehr unsicher waren. Die selbsternannten kompetenten weisen für die spezifischen Amorphie-bezogenen Schlüsselworte ein Krippendorff’s alpha von -0.42 auf.
Die Übereinstimmung der unsicheren folgt hier:
Das kripp.alpha() kann auch mit anderen Formaten von Daten arbeiten. Sie müssen die Daten entsprechend Ihrem spezifischen Format anpassen, wenn sie nicht bereits im Matrixformat vorliegen.
7.5.3 Cohen’s kappa
Cohen (1960) hat \(\kappa\) als “coefficient of agreement” vorgeschlagen. Bei nominalen Skalen sind demnach zwei Aspekte relevant (Cohen, 1960):
\(p_o\) = der Anteil der Fällen, in denen die Urteile übereinstimmen
\(p_c\) = der Anteil der Fälle, in denen ein übereinstimmendes Urteil zufällig zu erwarten wäre.
\[\kappa = \frac {p_o - p_c}{1-p_c}\] Eine zentrale Frage ist die Bestimmung der Häufigkeit durch Zufall, da sich die Annahmen Wahrscheinlichkeitsfunktion unterscheiden, je nachdem, ob es sich um die gemeinsame Häufigkeit (“cooccurence of frequencies”), die Übereinstimmung (“agreement coefficient”) oder die Gleichheit (“agreement equity”) handelt (Krippendorff, 1987, S. 121).
\[ \begin{array}{|c|c|c|c|c|} \hline \ & \text{} & \text{Experte 1} & \text{Experte 1} & \\ \ & \text{} & \text{K=0} & \text{K=1} & \\ \hline \text{Experte 2} & \text{K=0} & \text{a} & \text{b} & \sum {K_{Exp2}=0} \\ \text{Experte 2} & \text{K=1} & \text{c} & \text{d} & \sum{K_{Exp2}=1} \\ \hline \text{} & \text{} & \sum{K_{Exp1}=0} & \sum{K_{Exp1}=1} & \text{ Gesamt: (a+b+c+d)} \\ \hline \end{array}\]
Übereinstimmung der Bewerter liegt in den Zellen a und d vor, während keine Übereinstimmung in den Zellen b und c vorliegt.
Die Gesamtsumme der Urteile ergibt sich sowohl aus der Summe der Zeilensummen, als auch aus der Summe der Spaltensummen: \(N=a+b+c+d = a+c+b+d\)
Die Häufigkeit für Übereinstimmungen wird nach Cohen (1960, S. 45) durch die Summe der Diagonalen bestimmt als: \(f_o= a+d\)
Für die Zellen \(a\) und \(d\) wird die Häufigkeit der Übereinstimmung durch Zufall (\(a'\) und \(d'\)) durch das Produkt der Zeilen- und Spaltensummen bestimmt Cohen (1960, S. 38):
\(a'=\frac {(a+b) \cdot (a+c)}{N}\) \(d'=\frac {(c+d) \cdot (b+d)}{N}\)
\(f_c\) ergibt sich dann aus der Summe der Diagonalen als \(f_c= \frac {(a+b) \cdot (a+c)}{N} + \frac{(c+d) \cdot (b+d)}{N}\)
So kann \(\kappa\) über die Häufigkeiten bestimmt werden durch:
\(\kappa = \frac {f_o - f_c}{N-f_c}\)
Aus dem vorausgehenden Beispiel liegen die folgenden beobachteten Häufigkeiten vor:
\[\begin{array}{|c|c|c|c|c|} \hline \ & K_{Exp1}=0 & K_{Exp1}=1 & \text{Summe} \\ \hline \ K_{Exp2}=0 & \text{ a=0 } & \text{ b=7 } & \text{ 7 } \\ \ K_{Exp2}=1 & \text{ c=2 } & \text{ d=5 } & \text{ 7 }\\ \hline \text{Summe} & \text{2} & \text{12} & \text{14} \\ \hline \end{array}\]
Die beobachteten Häufigkeiten für Übereinstimmung ergeben sich aus der Diagonalen als:
\(f_o = 0 + 5 = 5\)
Die Häufigkeiten durch Zufall sind entsprechend:
\[\begin{array}{|c|c|c|c|c|} \hline \ & K_{Exp1}=0 & K_{Exp1}=1 & \text{Summe} \\ \hline \ K_{Exp2}=0 & a'= \frac {7 \cdot 2 }{N} & b'= \frac {7 \cdot 12 }{N} & \text{ 7 } \\ \ K_{Exp2}=1 & c'= \frac {7 \cdot 2 }{N} & d'= \frac {7 \cdot 12 }{N} & \text{ 7} \\ \hline \text{Summe} & \text{2} & \text{12} & \text{14} \\ \hline \end{array}\]
Und die Häufigkeiten durch Zufall sind:
\(f_c= 1 \cdot 6=6\)
\(\kappa= \frac {5-6}{14-6}= -0.125\)
Krippendorff (1987) (p.120) interpretiert den Agreement-Koeffizienten von Cohen (1960) in Form von Wahrscheinlichkeiten als:
\(\kappa= \frac {a-p_1p_2}{p-p_1p_2}=\frac {ad-bc}{\frac12(p_1q_2+q_1p_2)}\)
Die empirischen Wahrscheinlichkeiten entsprechen dann:
\[\begin{array}{|c|c|c|c|c|} \hline \ & 0 & 1 & \text{Summe} \\ \hline \text{0} & \text{ a=0.00 } & \text{ b=0.50 } & p_1= \text{ 0.50} \\ \text{1} & \text{ c=0.14 } & \text{ d=0.36 } & q_1 =\text{ 0.50 }\\ \hline \text{Summe} & p_2=\text{0.14} & q_2=\text{0.86} & \text{1.00} \\ \hline \end{array}\]
Unter Berücksichtigung dessen, dass \(K_{Exp1}=1=K_{Exp_2}\) in Zelle “d” vorliegt, ergibt sich dann:
\(\kappa=\frac{d-q_1 \cdot q_2}{p -p_1p_2} = \frac{0.36-0.43}{1-0.43}=-0.122\)
In allen Formen der Berechnung von \(\kappa\) liegt das Problem vor, dass ein identisches Urteil von zwei Bewerter (Identität) in einem {} resultiert.
\[\begin{array}{|c|c|c|c|c|} \hline \ & 0 & 1 & \text{Summe} \\ \hline \text{0} & \text{ a=0.00 } & \text{ b=0.00 } & p_1= \text{ 0.00 } \\ \text{1} & \text{ c=0.00 } & \text{ d=1.00 } & q_1 =\text{ 1.00 }\\ \hline \text{Summe} & p_2=\text{0.00} & q_2=\text{1.00} & \text{1} \\ \hline \end{array}\]
\(\kappa=\frac{1.00-1.00}{1.00-0.00} = \frac{0.00}{1.00}=0.00\)
7.6 Item Response Theorie
Im Folgenden zeigt ein Beispiel die Item-Respons-Analyse für 10 binäre kodierte Items auf. In der Item Response Theory (IRT) für binäre Daten werden Modelle verwendet, um die Wahrscheinlichkeit zu modellieren, dass ein Individuum mit bestimmten Merkmalen eine bestimmte Antwort auf ein Item gibt. Typischerweise werden binäre Daten als 0 oder 1 kodiert, wobei 0 für eine falsche Antwort oder ein Nichtwissen und 1 für eine richtige Antwort steht.
Das am häufigsten verwendete Modell für binäre Daten in der IRT ist das 1PL-Modell (One-Parameter Logistic Model) oder auch das Rasch-Modell genannt. Die Gleichung für das Rasch-Modell ist:
\[P(X_i = 1 | \theta) = \frac{1}{1 + e^{-a_i(\theta - b_i)}}\] wobei \(P(X_i = 1 | \theta)\) die Wahrscheinlichkeit ist, dass eine Person mit einem bestimmten Fähigkeitsniveau (\(\theta\)) eine richtige Antwort auf das Item \(i\) gibt
\(a_i\) ist der Diskriminationsparameter des Items \(i\), der angibt, wie gut das Item zwischen Personen mit unterschiedlichen Fähigkeitsniveaus unterscheidet.
\(b_i\) ist der Schwierigkeitsparameter des Items \(i\), der angibt, wie hoch das Fähigkeitsniveau sein muss, damit eine Person mit einer 50%igen Wahrscheinlichkeit das Item richtig beantwortet. und \(e\) ist die Basis des natürlichen Logarithmus.
Die Parameter \(a_i\) und \(b_i\) werden geschätzt, um die beobachteten Daten am besten zu modellieren. Dies geschieht typischerweise mit Hilfe von Schätzverfahren wie der Maximum-Likelihood-Methode.
In R können Modelle für binäre Daten mit der ltm (latent trait models) Bibliothek oder der mirt (multidimensional item response theory) Bibliothek geschätzt werden. Hier ist ein Beispiel für die Verwendung von ltm:
## Loading required package: ltm## Loading required package: msm## Loading required package: polycor##
## Attaching package: 'polycor'## The following object is masked from 'package:psych':
##
## polyserial##
## Attaching package: 'ltm'## The following object is masked from 'package:psych':
##
## factor.scores##
## Call:
## rasch(data = data)
##
## Model Summary:
## log.Lik AIC BIC
## -687.8916 1397.783 1426.44
##
## Coefficients:
## value std.err z.vals
## Dffclt.Item1 -1.2254 3.9084 -0.3135
## Dffclt.Item2 2.1676 5.9959 0.3615
## Dffclt.Item3 1.7106 4.9486 0.3457
## Dffclt.Item4 -4.3953 11.4236 -0.3848
## Dffclt.Item5 -1.0066 3.4811 -0.2892
## Dffclt.Item6 3.8124 9.9779 0.3821
## Dffclt.Item7 -1.4343 4.3439 -0.3302
## Dffclt.Item8 0.7079 2.9675 0.2385
## Dffclt.Item9 3.1306 8.3034 0.3770
## Dffclt.Item10 0.3095 2.4870 0.1244
## Dscrmn 0.0849 0.2158 0.3935
##
## Integration:
## method: Gauss-Hermite
## quadrature points: 21
##
## Optimization:
## Convergence: 0
## max(|grad|): 2.7
## quasi-Newton: BFGSDffclt.Item1 bis Dffclt.Item10 sind die Schwierigkeitsparameter für jedes der Items. Sie geben an, wie schwierig es ist, das jeweilige Item zu beantworten. Positive Werte zeigen an, dass das Item schwieriger ist, während negative Werte darauf hinweisen, dass das Item einfacher ist.
Dscrmn ist der Diskriminationsparameter des Rasch-Modells. Er gibt an, wie gut das Gesamtmodell zwischen Personen mit unterschiedlichen Fähigkeiten unterscheidet. Ein höherer Wert deutet auf eine höhere Diskriminationsfähigkeit hin.
Integration gibt Informationen über das verwendete Integrationsverfahren an. In diesem Fall wurde die Gauss-Hermite-Methode verwendet, um die numerische Integration durchzuführen, und es wurden 21 Quadraturpunkte verwendet.
Optimization gibt Informationen zur Optimierung des Modells.
Convergence ist ein Maß dafür, ob das Optimierungsverfahren konvergiert ist. Ein Wert von 0 bedeutet, dass das Verfahren erfolgreich konvergiert ist.
max(|grad|) ist der maximale Betrag des Gradienten während des Optimierungsvorgangs. Ein hoher Wert könnte auf Probleme mit der Konvergenz hinweisen.
quasi-Newton gibt an, welcher Algorithmus zur Optimierung verwendet wurde. In diesem Fall wurde das BFGS-Verfahren (Broyden-Fletcher-Goldfarb-Shanno) verwendet, was ein quasi-Newton-Verfahren ist.
Die Item-Response Analyse kann auch für 5-stufige Items durchgeführt werden:
## Loading required package: mirt## Loading required package: stats4## Loading required package: lattice##
## Attaching package: 'mirt'## The following object is masked from 'package:ltm':
##
## Science## The following objects are masked from 'package:eRm':
##
## itemfit, personfit## Iteration: 1, Log-Lik: -1683.151, Max-Change: 1.93227Iteration: 2, Log-Lik: -1602.718, Max-Change: 1.13734Iteration: 3, Log-Lik: -1582.962, Max-Change: 0.79333Iteration: 4, Log-Lik: -1576.106, Max-Change: 0.37447Iteration: 5, Log-Lik: -1572.340, Max-Change: 0.56549Iteration: 6, Log-Lik: -1569.595, Max-Change: 0.63333Iteration: 7, Log-Lik: -1567.800, Max-Change: 0.24129Iteration: 8, Log-Lik: -1566.200, Max-Change: 1.18104Iteration: 9, Log-Lik: -1564.464, Max-Change: 0.27508Iteration: 10, Log-Lik: -1564.065, Max-Change: 6.06146Iteration: 11, Log-Lik: -1560.870, Max-Change: 0.12973Iteration: 12, Log-Lik: -1559.996, Max-Change: 0.54563Iteration: 13, Log-Lik: -1559.070, Max-Change: 0.48609Iteration: 14, Log-Lik: -1558.339, Max-Change: 1.39993Iteration: 15, Log-Lik: -1557.330, Max-Change: 0.40313Iteration: 16, Log-Lik: -1557.105, Max-Change: 3.15686Iteration: 17, Log-Lik: -1555.764, Max-Change: 0.33848Iteration: 18, Log-Lik: -1555.213, Max-Change: 1.23298Iteration: 19, Log-Lik: -1554.279, Max-Change: 0.53233Iteration: 20, Log-Lik: -1553.726, Max-Change: 1.36828Iteration: 21, Log-Lik: -1552.926, Max-Change: 0.54944Iteration: 22, Log-Lik: -1552.536, Max-Change: 2.09007Iteration: 23, Log-Lik: -1551.636, Max-Change: 0.55867Iteration: 24, Log-Lik: -1551.221, Max-Change: 1.81951Iteration: 25, Log-Lik: -1550.445, Max-Change: 0.53952Iteration: 26, Log-Lik: -1550.093, Max-Change: 2.10801Iteration: 27, Log-Lik: -1549.562, Max-Change: 0.56341Iteration: 28, Log-Lik: -1549.452, Max-Change: 2.71339Iteration: 29, Log-Lik: -1549.024, Max-Change: 0.49387Iteration: 30, Log-Lik: -1548.807, Max-Change: 1.90727Iteration: 31, Log-Lik: -1548.519, Max-Change: 1.06094Iteration: 32, Log-Lik: -1548.356, Max-Change: 1.19557Iteration: 33, Log-Lik: -1548.218, Max-Change: 1.59158Iteration: 34, Log-Lik: -1548.070, Max-Change: 0.84550Iteration: 35, Log-Lik: -1547.970, Max-Change: 2.76180Iteration: 36, Log-Lik: -1547.843, Max-Change: 0.62294Iteration: 37, Log-Lik: -1547.806, Max-Change: 1.73154Iteration: 38, Log-Lik: -1547.717, Max-Change: 0.27357Iteration: 39, Log-Lik: -1547.687, Max-Change: 0.00916Iteration: 40, Log-Lik: -1547.687, Max-Change: 0.00913Iteration: 41, Log-Lik: -1547.682, Max-Change: 0.00103Iteration: 42, Log-Lik: -1547.680, Max-Change: 0.00050Iteration: 43, Log-Lik: -1547.680, Max-Change: 0.00018Iteration: 44, Log-Lik: -1547.680, Max-Change: 0.00002## F1 h2
## Item1 0.8613 0.74189
## Item2 0.8367 0.69999
## Item3 0.1814 0.03290
## Item4 0.2975 0.08850
## Item5 0.1105 0.01221
## Item6 0.4840 0.23424
## Item7 0.2247 0.05047
## Item8 0.1163 0.01351
## Item9 0.1682 0.02831
## Item10 0.0334 0.00112
##
## SS loadings: 1.903
## Proportion Var: 0.19
##
## Factor correlations:
##
## F1
## F1 1Das Ergebnis zeigt die Zusammenfassung eines IRT-Modells.
F1: ist die Schätzung des Faktorscores für den latenten Faktor (engl. latent trait) für jedes Item. Der Faktorscore gibt an, wie stark ein bestimmtes Item mit dem latenten Faktor F1 verbunden ist. Positive Werte zeigen an, dass höhere Werte des latenten Faktors mit höheren Reaktionen auf das Item verbunden sind, während negative Werte das Gegenteil bedeuten.
h2: ist der Anteil der Varianz des Items, der durch den latenten Faktor erklärt wird, der hier als “Communality” bezeichnet wird. Es gibt an, wie gut das jeweilige Item von dem latenten Faktor F1 erklärt wird. Ein Wert nahe bei 1 deutet darauf hin, dass das Item sehr gut durch den latenten Faktor erklärt wird, während ein Wert nahe bei 0 darauf hinweist, dass der Faktor wenig zur Erklärung der Varianz des Items beiträgt.
SS loadings: ist die Summe der quadratischen Ladungen (engl. sum of squares loadings) für alle Items auf den Faktor. Es gibt die Gesamtvarianz an, die durch den latenten Faktor erklärt wird.
Proportion Var: ist der Anteil der Gesamtvarianz, der durch den Faktor erklärt wird. In diesem Fall beträgt er 0,139, was bedeutet, dass der Faktor F1 etwa 13,9% der Gesamtvarianz erklärt. Factor correlations: Dieser Abschnitt gibt die Korrelationen zwischen den Faktoren an. Da es sich um ein unifaktorielles Modell handelt (nur ein Faktor), ist die Korrelation des Faktors F1 mit sich selbst immer 1.
Insgesamt zeigen diese Ergebnisse, wie jedes Item mit dem latenten Faktor in Verbindung steht, wie viel Varianz durch diesen Faktor erklärt wird und wie stark die Beziehung zwischen den Faktoren ist.
7.7 Entscheidungsparadoxon
Entscheidungen basieren in der Regel auf dem Abwägen der verfügbaren Informationen. Dieser Prozess umfasst das Sammeln, Bewerten und Analysieren von Daten, um die bestmögliche Entscheidung zu treffen. Oftmals können neue Informationen dazu führen, dass getroffene Entscheidungen überdacht und geändert werden. Dies ist in der Regel von Vorteil, da zusätzliche Datenpunkte und Erkenntnisse eine genauere Einschätzung der Situation ermöglichen.
Es gibt jedoch Situationen, in denen es nicht leicht nachvollziehbar ist, warum eine Änderung der Entscheidung gegenüber dem Beibehalten der ursprünglichen Entscheidung vorteilhaft sein sollte. Ein klassisches Beispiel hierfür ist das Monty-Hall-Problem, ein Paradoxon der Wahrscheinlichkeitsrechnung. Bei diesem Problem scheint es auf den ersten Blick irrational, die ursprüngliche Entscheidung zu ändern.
In einer bekannten Fernsehshow wurden Kandidaten vor die Wahl gestellt, eines aus drei verschlossenen Toren auszuwählen. Dabei befinden sich hinter zwei Toren Nieten (Zonk) und hinter einem Tor befindet sich ein Hauptgewinn (ein Auto).
Nachdem sich der Kandidat für ein Tor entschieden hat, öffnet der Moderator, der weiß, was sich hinter den Toren befindet, eines der beiden Tore, hinter der sich kein Gewinn befindet. Danach gibt der Moderator dem Kandidaten die Möglichkeit, seine ursprüngliche Wahl zu ändern und das andere noch geschlossene Tor zu wählen.
Ist es für den Kandidaten von Vorteil, bei seiner ursprünglichen Wahl bleiben? Oder sollte er die Tür wechseln, um seine Gewinnchancen zu maximieren?
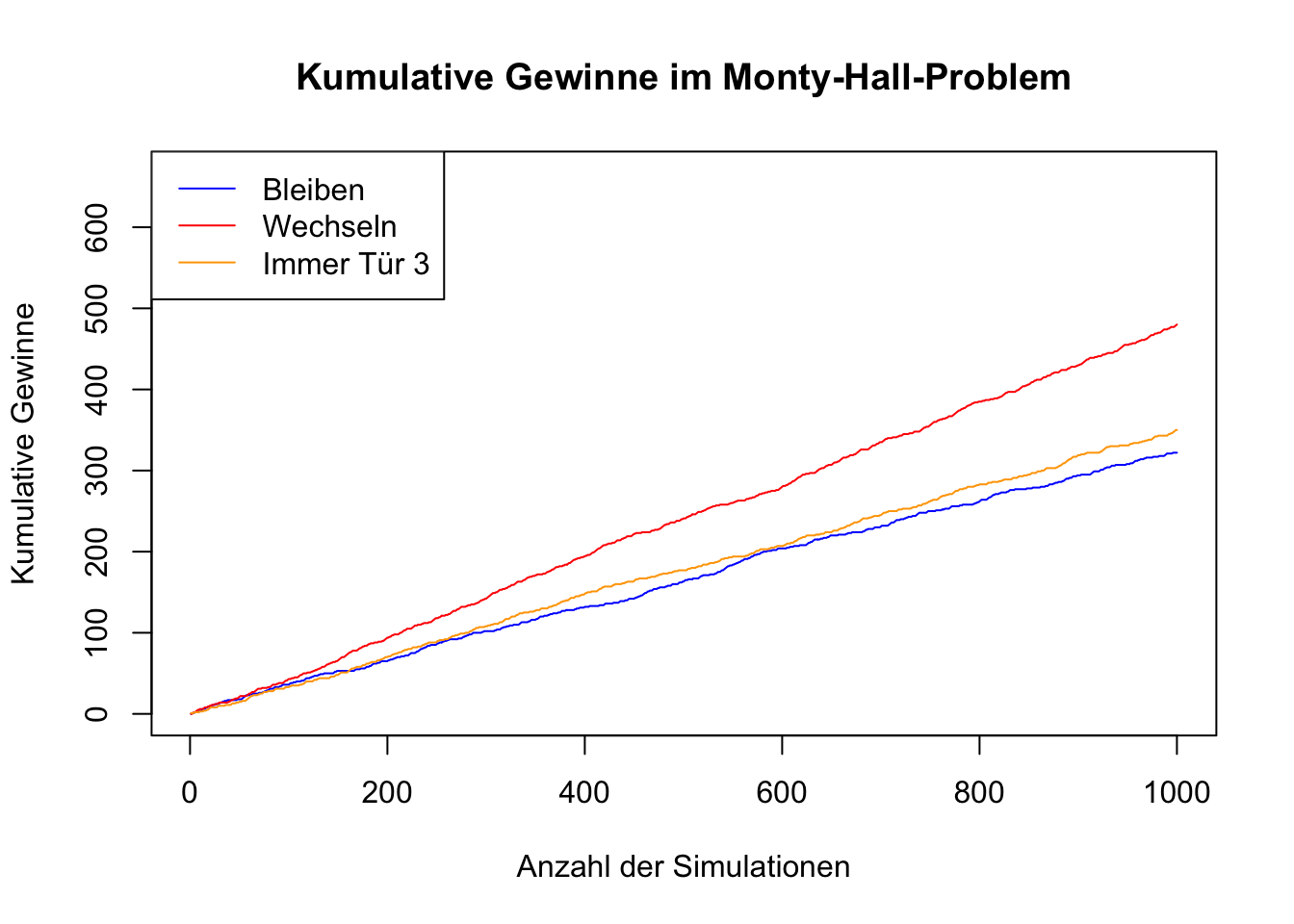
## Gesamte Gewinne durch Bleiben bei der ersten Wahl (zufällig): 322## Gesamte Gewinne durch Bleiben bei der ersten Wahl (immer Tür 3): 350## Gesamte Gewinne durch Wechseln der Wahl (zufällig): 480Dieses Paradoxon verdeutlicht, dass Intuition und Wahrscheinlichkeitsrechnung manchmal im Widerspruch stehen können und dass eine tiefere mathematische Analyse notwendig ist, um die bestmögliche Entscheidung zu treffen.
Wenn der Kandidat im ersten Schritt die richtige Tür gewählt hat und der Moderator öffnet eine Tür, hinter der eine Niete ist, ändert sich für den Kandidaten nichts, wenn er bei der Tür bleibt, für die er sich entschieden hatte. Aber in zwei von drei Fällen wird er eine falsche Tür gewählt haben.
Falls der Kandidat eine falsche Tür gewählt hat, kann er dies zwar noch nicht wissen, aber wenn er zwischen zwei Türen entscheidet, steigert er seine Chance, wenn er die Tür wechselt.
Durch das Wechseln nutzt der Kandidat die Situation, in denen er bei seiner ersten Wahl falsch lag (was in 2 von 3 Fällen der Fall ist), und korrigiert seine Wahl basierend auf den neuen Informationen, die durch das Öffnen einer Tür durch den Moderator verfügbar werden.
Wenn der Kandidat zwei Türen zur Wahl hat,kann der Eindruck entstehen, dass er eine 50:50-Chance hat, aber dies ist die Fehlannahme im Monty-Hall-Problem. Die tatsächlichen Wahrscheinlichkeiten basieren auf bedingter Wahrscheinlichkeit, die die ursprünglichen Wahrscheinlichkeiten berücksichtigt.
Obwohl nach dem Öffnen einer Tür nur noch zwei Türen übrig sind entspricht die “sichtbare” Wahrscheinlichkeit (50:50) nicht die “wirkliche” Wahrscheinlichkeit. Die ursprüngliche Wahl beeinflusst die bedingten Wahrscheinlichkeiten:
Wenn die erste Wahl falsch war (2/3 Wahrscheinlichkeit), gewinnt der Kandidat durch den Wechsel.
Wenn die erste Wahl richtig war (1/3 Wahrscheinlichkeit), verliert der Kandidat durch den Wechsel.
Durch einen Wechsel steigert der Kandidat also die Gewinn-Wahrscheinlichkeit, in zwei von drei Fällen (wenn die erste Wahl falsch war) und reduziert die Gewinnwahrscheinlichkeit nur in einem von drei Fällen (wenn die erste Wahl richtige war) nur in einem von drei Fällen.
Die bedingten Wahrscheinlichkeiten lassen sich auch mathematisch durch den Satz von Bayes berechnen, der die bedingte Wahrscheinlichkeit beschreibt:
- \(A\): Das Auto ist hinter dem ursprünglich gewählten Tor
- \(B\): Der Moderator öffnet ein anderes Tor und zeigt eine Niete.
Wir wollen \(P(A|B)\) berechnen, die bedingte Wahrscheinlichkeit, dass das Auto hinter dem ursprünglich gewählten Tor ist, gegeben, dass der Moderator eine Niete zeigt.
Die Bayes-Formel lautet:
\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]
Hier setzen wir die Wahrscheinlichkeiten ein:
- \(P(A)\): Die Wahrscheinlichkeit, dass das Auto hinter dem ursprünglich gewählten Tor ist, beträgt \(\frac{1}{3}\).
- \(P(B|A)\): Die Wahrscheinlichkeit, dass der Moderator eine Niete zeigt, gegeben, dass das Auto hinter dem ursprünglich gewählten Tor ist, beträgt 1. (Der Moderator wird immer eine Niete zeigen, da er weiß, wo sich das Auto befindet.)
- \(P(B)\): Die Gesamtwahrscheinlichkeit, dass der Moderator eine Niete zeigt. Diese kann aus den zwei möglichen Fällen berechnet werden:
- Das Auto ist hinter dem ursprünglich gewählten Tor (\(\frac{1}{3}\) Wahrscheinlichkeit), und der Moderator zeigt eine der zwei Nieten (Wahrscheinlichkeit 1).
- Das Auto ist nicht hinter dem ursprünglich gewählten Tor (\(\frac{2}{3}\) Wahrscheinlichkeit), und der Moderator zeigt das einzige Tor, dass eine Niete enthält (Wahrscheinlichkeit 1).