Kapitel 5 Datenanalyse
5.1 Hypothese
Die empirische Forschung verfolgt grundlegende Ziele wie Beschreibung, Erklärung und Nachweis von Phänomenen. Wenn ein Forscher über das reine Beschreiben hinausgehen und durch Datenanalyse auch Erklärungen und Nachweise liefern möchte, benötigt er eine Hypothese zur Struktur der Daten. Eine Hypothese ist eine Aussage, die die Vorstellung des Forschers über einen Sachverhalt darstellt und prinzipiell untersucht werden kann.
Ein Beispiel aus dem Bereich der wirtschaftswissenschaftlichen Konzepte veranschaulicht dies: Gemäß der Prinzipal-Agenten-Theorie (Jensen, 2000; Jensen & Meckling, 1976) wird angenommen, dass Kooperationspartner nicht zögern, ihre eigenen egoistischen Interessen gegenüber dem Partner mit allen Mitteln durchzusetzen.
Es ist ebenfalls aus der Literatur bekannt, dass in Beziehungen, in denen opportunistisches Verhalten wahrgenommen oder erwartet wird, ein geringeres Vertrauen in den Kooperationspartner besteht. Zudem wird in der Literatur darauf hingewiesen, dass komplexe Verträge ausgearbeitet werden, um opportunistisches Verhalten zu reduzieren (Jones & Bouncken, 2008, S. 106). Der Kontext des Opportunismus bietet somit eine Grundlage für eine Hypothese über den Zusammenhang zwischen Vertragskomplexität und Vertrauen. Die resultierende Hypothese lautet daher:
\(H_1\): ‘Steigende Vertragskomplexität steigert das Vertrauen in den Kooperationspartner.’
Eine Hypothese ist also ein Satz, der eine spezifische Aussage zu einem beobachtbaren und nachweisbaren Sachverhalt macht, der meistens aus einer Theorie abgeleitet ist und idealerweise für die gesamte Population (Grundgesamtheit) gelten soll.
Auch wenn sich in der Stichprobe herausstellt, dass diese Aussage zutrifft, könnte dies rein zufällig geschehen, selbst wenn sie im Allgemeinen nicht korrekt ist. In der traditionellen Statistik wird diesem Risiko durch die Verwendung einer Nullhypothese begegnet, die die Aussage der Hypothese negiert (Wendt, 1983).
Eine entsprechende Nullhypothese lautet demnach \(H_0\): ‘Es besteht kein Zusammenhang zwischen Vertragskomplexität und Vertrauen.’
Mit der eigentlichen Teststatistik bestimmt man dann die Wahrscheinlichkeit der Nullhypothese anhand der vorliegenden Daten. Ist die Wahrscheinlichkeit für die Richtigkeit der Nullhypothese gering und wird diese verworfen, wird dies als Beleg für die Akzeptanz ihrer Alternative (also der ursprünglichen Hypothese) angesehen.
An dieser Stelle kann angemerkt werden, dass innerhalb der Wissenschaften verschiedene Sichtweisen auf Wahrscheinlichkeit existieren. Die Auffassung von Wahrscheinlichkeit in der klassischen Statistik wird als ‘frequentistisch’ bezeichnet und Wahrscheinlichkeit wird dabei als Grenzwert einer relativen Häufigkeit dargestellt (Wendt, 1983):
\[p(X)= \lim_{n \to \infty} \frac {H\ddot{a}ufigkeit \: von \: X \: unter \: n \: Beobachtungen}{n}\]
Diese Wahrscheinlichkeit wird anhand der Häufigkeit eines Ereignisses in einer Population oder in einer Stichprobe aus der Population bestimmt. Das traditionelle Paradigma betrachtet Populationsparameter wie Mittelwerte, Standardabweichungen und Zusammenhangsmaße wie Korrelations- und Regressionskoeffizienten als unbekannte, aber feste Größen der Grundgesamtheit. Das Ziel der Parameterschätzung besteht darin, Vertrauensintervalle für die Punktschätzung dieser Parameter in Stichproben zu finden (Rupp, Dey & Zumbo, 2004).
Hypothesen werden empirisch unterstützt, wenn die relative Häufigkeit der Nullhypothese unwahrscheinlich ist. Die Nullhypothese entspricht der gegenteiligen Aussage der Hypothese. Falls die Hypothese beispielsweise einen positiven Zusammenhang postulliert, wird die Nullhypothese überprüft, dass kein bzw. ein zufälliger Zusammenhang besteht. Wenn die relative Häufigkeit der Nullhypothese geringer als die zuvor festgelegte Wahrscheinlichkeit von \(\alpha = 0.05\) ist, ist es unwahrscheinlich, dass die Nullhypothese zutrifft.
Basierend auf der Unwahrscheinlichkeit der Nullhypothese wird die Hypothese dann auf einem Signifikanzniveau von \(\alpha ≤ 0.05\) akzeptiert. Das bedeutet, dass wir unsere Idee als gültig ansehen, weil die Wahrscheinlichkeit, dass sie falsch ist, weniger als 5% beträgt.
5.2 Hypothesenprüfung
Von einem logischen Standpunkt aus betrachtet, handelt es sich dabei um eine Entscheidung nach dem Schlussprinzip des sogenannten Modus Tollens (Wendt, 1983). Dieses Prinzip ist eine Regel der deduktiven Logik, die sich mit der korrekten Ableitung von Aussagen aus gegebenen anderen Aussagen befasst.
Aussagen werden in den Sprach- und Kognitionswissenschaften als Propositionen bezeichnet und bilden die kleinstmöglichen Wissenseinheiten ab, die entweder wahr oder falsch sein können (Westermann, 2000, S. 69).
In der Aussagenlogik werden Aussageformen, die Implikationen von Prämissen beinhalten als Schlussformen bezeichnet und stellen Regeln dar, nach denen man von wahren Aussagen zu anderen wahren Aussagen gelangen kann. Der modus tollens ist eine solche allgemeingültige Schlussformel:
\[[(A \to B) \wedge \neg B] \to \neg A \]
Er definiert die implikative Verknüpfung von B folgt logisch aus A, formuliert mit \((A \to B)\). Wenn die Aussage A wahr ist, dann muss zwangsläufig auch die Aussage B wahr sein.
Zur Veranschaulichung solcher Schlussformen werden Wahrheitstabellen verwendet. Diese weisen aber auch darauf hin, dass logische Schlussformen nicht immer mit dem Alltagsverständnis von ‘wenn - dann’ Beziehungen einhergehen. So ist beispielsweise die Implikation B folgt logisch aus A \((A \to B)\) immer dann wahr, wenn A falsch ist. Dies betrifft in der Wahrheitstabelle die Zeilen 2 und 4. Definitionsgemäß ist die Implikation B folgt logisch aus A \((A \to B)\) nur dann als falsch anzusehen, wenn A wahr und B falsch ist (Westermann, 2000, S. 73).
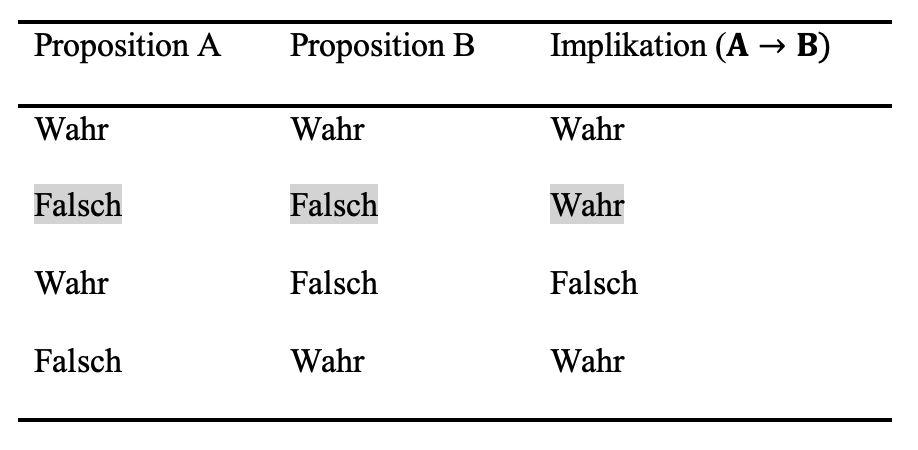
Der modus tollens regelt also den Geltungsbereich der Implikation B folgt logisch aus A ist wahr \((A \to B)\) und \((\wedge)\) die Aussage B ist falsch. Demnach schließt man aus der Unwahrheit von B unter der Bedingung, dass B folgt logisch aus A gilt \((A\to B)\), das A falsch ist (Zeile 2).
Übertragen auf das Problem der Hypothesenentscheidung ergibt sich die folgende Darstellung.
Die Hypothese ‘Steigende Vertragskomplexität steigert das Vertrauen in den Kooperationspartner’ soll Unterstützung finden. Dem gegenüber wird die Nullhypothese \((H_0)\) getestet, dass gar kein Zusammenhang besteht. Die Nullhypothese beinhaltet nun auch spezifische Annahmen über die Verteilung (Mittelwert, Standardabweichung) und Zusammenhangsmaße (Kovarianz) der Daten in der Stichprobe \((D_0)\). Entsprechend der Normalverteilungsannahme wäre dies: das Zusammenhangsmaß ist normalverteilt und hat einen Mittelwert von Null (kein Zusammenhang).
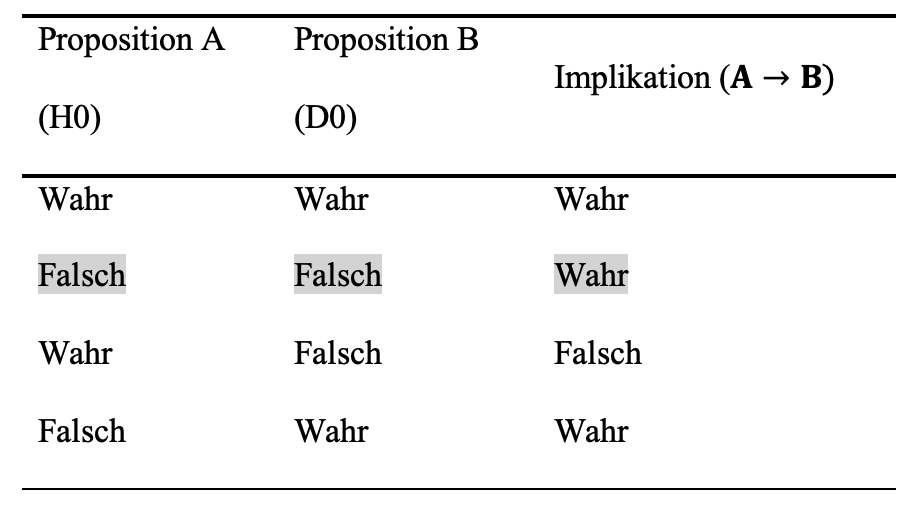
Aus Zeile 1 der Wahrheitstabelle können wir folgendes entnehmen: die Implikation B folgt logisch aus A ist wahr \((A\to B)\), \(H_0\) (die Nullhypothese) und \(D_0\) (das damit erwartete mittlere Zusammenhangsmaß in \(D_0\) von Null) sind wahr.
Zeile 2 zeigt auf: Die Implikation B folgt logisch aus A ist wahr \((A\to B)\), wobei \(H_0\) falsch ist (es ist also die falsche Nullhypothese) und \(D_0\) ist ebenso falsch (das Zusammenhangsmaß in \(D_0\) ist ungleich Null).
In Zeile 3 ist: Die Implikation B folgt logisch aus A \((A\to B)\) definitionsgemäß falsch, wenn A (die Nullhypothese \(H_0\)) wahr und B falsch ist (also ein Zusammenhangsmaß ungleich Null aufweist).
Aus Zeile 4 lässt sich ablesen, dass: Die Implikation B folgt logisch aus A ist auch wahr \((A \to B)\), wenn A (die Nullhypothese \(H_0\)) falsch und B (Zusammenhangsmaß gleich Null) wahr ist.
Nach dem modus tollens wird geschlossen, dass wenn das Zusammenhangsmaß ungleich Null ist und unter der Bedingung, dass B folgt logisch aus A gilt \((A\to B)\), dass die Nullhypothese falsch ist. (Dies entspricht der zweiten Zeile der Wahrheitstabelle).
Auch Forscher unterliegen häufiger erheblichen Schwierigkeiten mit Folgerungen, die dem modus tollens entsprechen und sie schließen von der Zurückweisung der Nullhypothese (A ist falsch) auf ein Zusammenhangsmaß das ungleich Null ist (B ist unwahr) (Anderson, 1996, S. 304–308), was aber nicht logisch zwingend (Westermann, 2000, S. 80) und in Zeile 3 dargestellt ist.
Mit anderen Worten, wenn die Implikation B folgt logisch aus A \((A\to B)\) gilt (Zeilen 1, 2 und 4) und wenn B falsch ist (Zeilen 2), lässt sich daraus die Falschheit von A ableiten (Modus tollens).
Ist die Aussage, dass die Verteilung der Daten \(D_0\) der Annahme aus \(H_0\) folgen, falsch (bzw. ist die Wahrscheinlichkeit zu gering), so wird entschieden, dass die Nullhypothese \(H_0\) falsch ist und ‘Quoniam tertium non datur’ damit darf die Alternativhypothese (als ihr Gegenteil) als richtig angesehen werden (Wendt, 1983). Dies folgt dem logischen Grundprinzip, nach dem für eine Aussage nur die Aussage selbst oder ihr Gegenteil gelten kann. Eine dritte Möglichkeit, etwas, das weder die Aussage selbst noch ihr Gegenteil ist, kann es paradigmatisch nicht geben.
Zusammenfassend wurde erläutert, wie neue Erkenntnisse durch die Falsifikation, also die Ablehnung der Nullhypothese, gewonnen werden: \([(\neg H_0) \to H_A]\). Wenn die Nullhypothese nicht abgelehnt werden kann, folgt daraus jedoch nicht zwangsläufig, dass die Nullhypothese “wahr” ist. (Wendt, 1983).
5.3 Datenaufbereitung
Daten liegen uns gewöhnlich in Form von Datentabellen vor. Jede Zeile repräsentiert dabei eine einzelne Befragung, wobei die erste Spalte eine eindeutige ID enthält, die es ermöglicht, diesen Fall mit anderen Tabellen zu verknüpfen.
Die folgenden Spalten, von J1 bis J9, beziehen sich auf den Abschnitt des Fragebogens “J - Digitale Orientierung unseres Unternehmens” und die darin enthaltenen Items J1 bis J9. Die präsentierten Daten stammen aus realen Erhebungen des Jahres 2019. Zum Beispiel hat der Befragte mit der ID 195 auf die Aussage “Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen” mit ‘5’ geantwortet, was “voll zutreffend” bedeutet. Leere Zellen, wie sie beim Befragten mit der ID 201 zu sehen sind, zeigen an, dass dieser Befragte (aus welchen Gründen auch immer) an dieser Stelle keine Angaben gemacht hat.
\[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{R_ID}&\text{...}&\text{J1}&\text{J2}&\text{J3}&\text{J4}&\text{J5}&\text{J6}&\text{J7}&\text{J8}&\text{J9}&\text{...}\\ \hline \text{195} & \text{...} & \text{5} & \text{5} & \text{5} & \text{5} & \text{5} & \text{5} & \text{5} & \text{5} & \text{5} \\ \text{196} & \text{...} & \text{3} & \text{3} & \text{3} & \text{3} & \text{3} & \text{3} & \text{3} & \text{3} & \text{3} \\ \text{197} & \text{...} & \text{5} & \text{4} & \text{4} & \text{5} & \text{4} & \text{4} & \text{4} & \text{5} & \text{5} \\ \text{198} & \text{...} & \text{2} & \text{3} & \text{2} & \text{2} & \text{3} & \text{2} & \text{1} & \text{1} & \text{2} \\ \text{199} & \text{...} & \text{3} & \text{4} & \text{4} & \text{4} & \text{5} & \text{4} & \text{3} & \text{4} & \text{4} \\ \text{200} & \text{...} & \text{5} & \text{5} & \text{1} & \text{1} & \text{1} & \text{1} & \text{1} & \text{1} & \text{1} \\ \text{201} & \text{...} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} & \text{...} \\ \hline \end{array}\]
Wenn die Tabelle spaltenweise betrachtet wird, zeigt sich zum Beispiel, dass 50 Prozent der Befragten (drei von sechs) die Aussage “Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen” mit “eher” oder “voll zutreffend” beantwortet haben, während nur 17 Prozent (ein Fall von sechs) sie mit “eher nicht” oder “nicht zutreffend” bewertet haben.
Weitere statistische Kennwerte können spaltenweise ermittelt werden. Das arithmetische Mittel ist das gängigste Maß für die zentrale Tendenz (Bortz, 1993, S. 38). Es wird berechnet, indem die Summe aller Einzelwerte durch die Anzahl der Werte geteilt wird.
\[ \overline{x}= \frac {1}{n} \sum_{k=1}^{n} x_k\]
Es wird bereits hier deutlich, dass die ursprüngliche Skala (von ‘trifft nicht zu’ bis ‘trifft vollständig zu’) begrenzte Interpretationsmöglichkeiten bietet. Die Aussage “Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen” wird ‘im Durchschnitt’ mit 3,8 beantwortet, wobei die Skala von 1 bis 5 reicht.
Ideal formuliert oder skaliert sollten Items so gestaltet sein, dass der durchschnittliche Wert in großen Zufallsstichproben dem Skalenmittelwert entspricht. Das zweite Item J2 “Wir arbeiten daran, neue digitale Geschäftsmodelle zu entwickeln” wurde beispielsweise von keinem der sieben Befragten mit “trifft nicht zu” oder “trifft eher nicht zu” beantwortet.
Die resultierenden Einschränkungen der Variabilität in den Antworten können später zu Problemen bei bestimmten Analyseverfahren führen.
Die Varianz \((s^2 bzw. \sigma^2)\) ist eines der gängigsten Maße zur Kennzeichnung der Variabilität einer Verteilung. Sie ergibt sich aus der Summe der quadrierten Abweichungen aller Messwerte vom arithmetischen Mittel, dividiert durch die Anzahl der Messwerte (Bortz, 1993, S. 41).
\[ \sigma^2 = s^2 = \sum_{i=1}^{n} (x_i-\overline{x})^2\]
Die Standardabweichung (auch als Streuung bezeichnet) ergibt sich aus der Wurzel der Varianz und beschreibt die durchschnittliche Abweichung vom arithmetischen Mittel.
\[ \sigma = sd = \sqrt {\sigma^2}\]
5.4 Heterogenitätsmaße
Eine Anwendung der Standardabweichung ist der Einsatz als Heterogenitätsmaß. Bei Analysen zum Einfluss von Gruppenheterogenität steht der Forschende nämlich zuerst vor der Frage, wie die individuellen Merkmale auf Teamebene aggregiert werden, um eine entsprechende Bewertung zu ermöglichen. Der klassische Ansatz definiert Diversität als Gruppenvariable, die den Grad der Unterschiedlichkeit innerhalb einer Population angibt. Eine Grundlage für die Bestimmung solcher Gruppenmerkmale bilden Verteilungsmaße der individuellen Merkmale, z.B. Streuungsmaße wie die Standardabweichung (Ratzmann, 2016, S. 25).
Im folgenden Beispiel soll die Diversität des Alters innerhalb von zwei Gruppen verglichen werden. Welche Gruppe weist die höhere Altersdiversität auf?
\[\begin{array}{|c|c|c|} \hline & \text{Gruppe 1} & \text{Gruppe 2} \\ \hline \text{Person 1} & \text{20 Jahre} & \text{20 Jahre} \\ \text{Person 2} & \text{23 Jahre} & \text{28 Jahre} \\ \text{Person 3} & \text{25 Jahre} & \text{32 Jahre} \\ \text{Person 4} & \text{36 Jahre} & \text{42 Jahre} \\ \text{Person 5} & \text{57 Jahre} & \text{57 Jahre} \\ \hline \end{array}\]
## Mittelwert Gruppe 1: 32.2## Standardabweichung Gruppe 1: 15.12283## Mittelwert Gruppe 2: 35.8## Standardabweichung Gruppe 2: 14.25482In beiden Gruppen sind die Mitglieder zwischen 20 und 57 Jahren alt. Im Durchschnitt ist die erste Gruppe etwas jünger (32 Jahre) als die zweite Gruppe (36 Jahre). Weil eine geringe Standardabweichung auf Homogenität des Alters innerhalb der Gruppe hinweisen kann, während eine hohe Standardabweichung hingegen Unterschiedlichkeit aufzeigt, könnte Gruppe 1 nicht nur als jüngere, sondern auch als die altersdiversere Gruppe beschrieben werden (\(SD_1=15.1\) vs. \(SD_2=14.3\)).
5.4.1 Blau’s Diversity-Index
Der Blau-Index (1977) quantifiziert die Diversität (Unterschiedlichkeit) innerhalb einer Gruppe. Der Index erreicht seinen Mindestwert (0), wenn es keine Varietät gibt, d. h. wenn alle Personen in dieselbe Kategorie eingestuft werden. Der Maximalwert hängt von der Anzahl der Kategorien ab und davon, dass Einzelpersonen in allen Kategorien gleichmäßig verteilt werden können.
\[ BI = 1 - ∑\limits_{i = 1}^k {p_i^2 } \] Dabei bezeichnet \(p_i\) den Anteil der Gruppenmitglieder in der i-ten Kategorie und \(k\) die Anzahl der Kategorien für das interessierende Merkmal.
Die Berücksichtigung der theoretischen Obergrenze sowie die Anpassung resultiert in einem Maß, das von 0 (Gleichheit) bis 1 (maximale Unterschiedlichkeit) reicht.
Angenommen, ein Top-Management-Team besteht aus zwei Personen und wir haben nur die Information einer Person befragt. Der Befragte kann seinen Bildungsabschluss auf einer Skala von 1 bis 7 angeben. Dabei bezeichnet 1) einen Hauptschulabschluss, 2) Realschule, 3) Abitur, 4) Bachelor, 5) Master, 6) Promotion und 7) die Habilitation.
Angenommen, das zweite Mitglied des TMT hat die gleiche Qualifikation wie der Befragte, dann antwortet er in der gleichen Kategorie. Es ist völlig egal, ob beide einen Hauptschulabschluss oder eine Habilitation vorweisen. Für den Blau-Index zählt nur die Gleichheit der Kategorie.
Falls beide einen Hauptschulabschluss vorweisen, ergibt sich für die sieben Kategorien (k=7):
\[p_1=1 \\ p_2=0 \\ p_3=0 \\ p_4=0 \\ p_5=0 \\ p_6=0 \\ p_7=0 \\ \] Die Aussage ist dann, dass 100 Prozent der TMT-Member (alle beide) den gleichen Abschluss aufweisen.
\[ BI = 1 - ∑\limits_{i = 1}^k {1^2 + 0^2 + 0^2 + 0^2 +0^2+0^2+0^2} \] Für den Fall, dass beide TMT-Mitglieder eine Habilitation erreicht hätten, resultiert lediglich eine Änderung in der Reihenfolge der Summanden, da die gleiche Ähnlichkeit vorliegt.
\[ BI = 1 - ∑\limits_{i = 1}^k { 0^2 + 0^2 + 0^2 +0^2+0^2+0^2+1^2} \]
Es ergibt sich in beiden Fällen: \[BI = 1- 1^2 = 0\] Dieser Wert kann aber nur dann resultieren, wenn wir entweder wissen oder annehmen, dass beide TMT-Mitglieder den gleichen Abschluss aufweisen.
Die zweite Möglichkeit besteht, zumindest theoretisch, in der Annahme, dass die beiden TMT-Mitglieder unterschiedliche Qualifikationen aufweisen. Dann ergibt sich in jedem Fall, dass die TMT-Mitglieder in zwei Kategorien mit jeweils einem Anteil von 50 Prozent vertreten sind. Im ersten Fall hat ein TMT-Mitglied (50%) einen Hauptschulabschluss und das zweite TMT-Mitglied (50%) weist eine Habilitation vor.
\[ BI = 1 - ∑\limits_{i = 1}^k { 0.5^2 + 0^2 + 0^2 +0^2+0^2+0^2+0.5^2} \] \[BI = 1- (0.25 + 0.25) = 0.5\] Der Blau-Index beträgt dann 0,5. Den gleichen Wert erhalten wir, wenn die beiden TMT-Mitglieder unterschiedliche Hochschul-Qualifikationen (z.B. Bachelor ist Kategorie 4 und Master ist Kategorie 5) aufweisen:
\[ BI = 1 - ∑\limits_{i = 1}^k { 0^2 + 0^2 +0^2 + 0.5^2 +0.5^2+0^2+0^2} \] \[BI = 1- (0.25 + 0.25) = 0.5\]
Bei einer Gruppengröße von 2 und 7 Kategorien kann der Blau-Index also theoretisch die folgenden Werte annehmen:
0 (wenn beide Mitglieder in derselben Kategorie sind)
0.5 (wenn die beiden Mitglieder in unterschiedlichen Kategorien sind)
Es gibt keine anderen möglichen Werte für den Blau-Index in dieser spezifischen Konstellation.
Bei drei oder mehr Mitgliedern im TMT kann der Blau-Index durch jeweils komplexere Kombinationen resultieren, und die Komplexität nimmt weiter zu, wenn die Anzahl der Kategorien steigt. In diesem Beispiel eignen sich die Kategorien nur bedingt. Durch eine unnötige Differenzierung von Kategorien wird die Diversität gegebenenfalls unnötig aufgebläht.
5.4.2 Rao-Stirling-Diversitätsmaß
Ein Diversitätsmaß, dass die euklidische Distanz (Satzes des Pythagoras) nutzt, ist das Rao-Stirling-Diversitätsmaß (Cassi L, 2017). Dieses Maß integriert die Dissimilarität oder Entfernung zwischen Kategorien mit ihren relativen Häufigkeiten. Die euklidische Distanz wird häufig verwendet, um die Dissimilarität zwischen Kategorien in einem multidimensionalen Raum zu berechnen.
Das Rao-Stirling-Diversitätsmaß kombiniert sowohl die Dissimilarität (oder Distanz) zwischen den Kategorien als auch deren relative Häufigkeiten, um die Diversität zu quantifizieren.
Das Rao-Stirling-Diversitätsmaß \(D\) wird nach der Gleichung:
\[ D = \sum_{i=1}^{n} \sum_{j=1}^{n} p_i p_j d_{ij} \]
bestimmt, wobei:
\(n\) die Anzahl der Kategorien ist,
\(p_i\) und \(p_j\) die Anteile der Kategorien \(i\) und \(j\) sind und
\(d_{ij}\) die Entfernung (Dissimilarität) zwischen den Kategorien \(i\) und \(j\) ist .
## Das Rao-Stirling-Diversitätsmaß innerhalb von Gruppe 1 beträgt: 6.96## Das Rao-Stirling-Diversitätsmaß innerhalb von Gruppe 2 beträgt: 7.045.4.3 Vergleich
Im Vergleich wird dieser drei Heterogenitätsmaße wird deutlich, dass die Entscheidung für das eine oder andere Maß von der Sichtweise und Intention des Forschers bestimmt wird.
## Die Standardabweichung (SD) innerhalb von Gruppe 1 beträgt: 15.12283## Die Standardabweichung (SD) innerhalb von Gruppe 2 beträgt: 14.25482## Der Blau-Index innerhalb von Gruppe 1 beträgt: 0.8## Der Blau-Index innerhalb von Gruppe 2 beträgt: 0.8## Das Rao-Stirling-Diversitätsmaß innerhalb von Gruppe 1 beträgt: 6.96## Das Rao-Stirling-Diversitätsmaß innerhalb von Gruppe 2 beträgt: 7.04Die gleiche Gruppenzusammensetzung lässt drei unterschiedliche Aussagen zu:
\[\begin{array}{|c|c|c|} \hline & \text{Gruppe 1} & \text{Gruppe 2} \\ \hline \text{Person 1} & \text{20 Jahre} & \text{20 Jahre} \\ \text{Person 2} & \text{23 Jahre} & \text{28 Jahre} \\ \text{Person 3} & \text{25 Jahre} & \text{32 Jahre} \\ \text{Person 4} & \text{36 Jahre} & \text{42 Jahre} \\ \text{Person 5} & \text{57 Jahre} & \text{57 Jahre} \\ \hline \text{SD} & \text{15.12} & \text{14.25} \\ \text{Blau-Index} & \text{0.80} & \text{0.80} \\ \text{Rao-Stirling} & \text{6.96} & \text{7.04} \\ \hline \end{array} \]
Auf Grundlage der Standardabweichung ist Gruppe 1 als altersdiverser einzuschätzen. Der Blau-Index weist hingegen darauf hin, dass sich beide Gruppen hinsichtlich der Altersdiversität gleichen. Der Rao-Stirling-Index beschreibt Gruppe 2 mit einer höheren Altersdiversität.
Mit der Intention, Diversität in Gruppen zu beschreiben, wird es zunächst notwendig, Formen der Unterschiedlichkeit zu verstehen und die angemessene Methode auszuwählen. Die Methode der Standardabweichung bietet eine Perspektive, in der die Individuen von dem Forscher als Gruppe betrachtet werden, unabhängig davon, ob sich die Individuen selbst als Gruppe wahrnehmen. Die Standardabweichung verdeutlicht, wie einheitlich die Gruppe in Bezug auf das betrachtete Merkmal ist.
Der Blau-Index zeigt auf, wie häufig Individuen der Gruppe die gleiche Merkmalsausprägung aufweisen, unabhängig davon, wie weit die einzelnen Merkmalsausprägungen (Kategorien) voneinander entfernt liegen.
Der Rao-Stirling-Index bestimmt die Merkmalsdifferenzen für die Individuen und zeigt auf, wie häufig geringe oder hohe Unterschiedlichkeit vorzufinden ist.
Der Dispersions-Ansatz zur Bestimmung von Unterschiedlichkeit bezeichnet die methodischen Ansätze, Heterogenität über die Verteilung von individuellen Merkmalen in Gruppen zu bestimmen.
Eine weitere Perspektive, die als Alignment-Ansatz bezeichnet wird, ist stärker auf die Anordnung von individuellen Merkmalen in merkmalshomogene Untergruppen ausgerichtet.
Dieses analytische Konzept ist im Kontext der Theorien zu sozialen Identität, der Selbstkategorisierung und dem Ähnlichkeits-Attraktions-Paradigma entwickelt und eignet sich, um Konflikte innerhalb von Gruppen durch Spannungslinien (sogenannte Faultlines), die zwischen Untergruppen entstehen, abzubilden (Ratzmann, 2016).
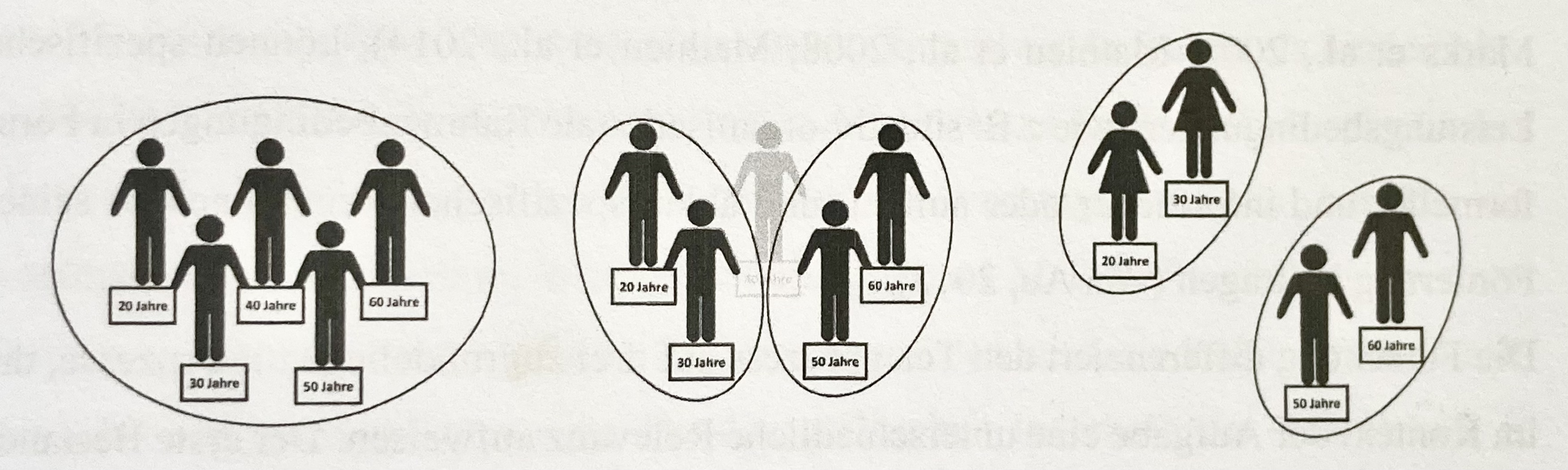
Diversität und Faultlines bezeichnen unterschiedliche Konzepte und ein hohes Maß an Diversität kann die Bildung von Faultlines erschweren. In der Abbildung wird aufgezeigt, dass sich die Altersstruktur (Mittelwert und Standardabweichung) links und mittig nur moderat unterscheiden. Der Alignment-Ansatz indiziert links keine Spannungslinie, weil sich dort keine homogenen Untergruppen bilden lassen. Verlässt eine Person die Gruppe (Mitte) resulitiert daraus ein hohes Potenzial für eine Spannungslinie (junge vs ältere). Diese Faultline wird rechts durch ein zweites Merkmal (junge Frauen vs. ältere Männer) verstärkt (Ratzmann, 2016).
5.5 Zusammenhangsmaße
Die Kovarianz (covariance) ist eine Messung des Zusammenhanges (association or relationship) zweier Variablen (Kenny, 2004, S. 17) oder anders formuliert die Kovarianz misst die gemeinsame (Ko)-Variation der Werte eines Variablenpaares (Dolic, 2010, S. 205). Mathematisch wird die Kovarianz als Erwartungswert der Abweichungen vom jeweiligen Populationsmittelwert zweier Variablen definiert (Kenny, 2004):
\[ E[(X-\mu_X)(Y-\mu_X)]\]
Dabei stellt E die Erwartung dar und die Populationsmittelwerte sind für Variable X durch \(\mu_X\) und für die Variable Y durch \(\mu_Y\) bezeichnet.
Zwei gebräuchliche Schreibweisen zur Bezeichnung von Kovarianzen sind: cov(x,y) und \(\sigma_{XY}\) (sigma). Eine unverzerrte Stichprobenschätzung der Kovarianz ergibt sich in Zufallsstichproben nach der dargestellten Gleichung, wobei \(M_X\) und \(M_Y\) die Stichprobenmittelwerte und N die Stichprobengröße darstellen (Kenny, 2004):
\[cov(x,y)=\frac{\sum(X-M_X)(Y-M_Y)}{N-1}\]
Aus unserer ursprünglichen Datentabelle, welche (die ID ausgeschlossen) neun Variablen J1 bis J9 beinhaltet, ergeben sich dem entsprechend 9x9 mögliche Kovarianzen, die sich in Form einer Kovarianzmatrix darstellen lassen. Dabei gilt per Definition, dass die Kovarianz einer Variablen mit sich selbst gleich der Varianz dieser Variable beträgt
\[cov(x,x)=var(x)=\sigma^2_x\] und die Kovarianz von Variablenpaar x - y gleich der Kovarianz von y - x ist.
\[cov(x,y)=cov(y,x)\]
## J1 J2 J3 J4 J5 J6 J7 J8 J9
## J1 1.77 1.0 0.43 0.67 -0.1 0.43 0.97 0.67 0.67
## J2 1.00 0.8 0.20 0.20 0.0 0.20 0.40 0.20 0.20
## J3 0.43 0.2 2.17 2.33 2.1 2.17 2.23 2.33 2.33
## J4 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67
## J5 -0.10 0.0 2.10 2.20 2.3 2.10 1.90 2.20 2.20
## J6 0.43 0.2 2.17 2.33 2.1 2.17 2.23 2.33 2.33
## J7 0.97 0.4 2.23 2.47 1.9 2.23 2.57 2.47 2.47
## J8 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67
## J9 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67Für die resultierende Kovarianzmatrix ergibt sich, dass die Diagonale von links oben nach rechts unten die Auto-Kovarianzen (also die Varianzen) darstellt. Die darüber und darunter liegenden Kovarianzen liegen in gespiegelter Form vor. Sollen Zusammenhänge zwischen Variablen nicht nur aufgezeigt, sondern hinsichtlich ihrer Signifikanz beurteilt werden, werden üblicherweise Korrelations-Matrizen anstelle der Kovarianz-Matrizen bestimmt. Die Korrelationskoeffizienten können hinsichtlich der Nullhypothese getestet werden, dass die wahre Korrelation gleich einem Wert von Null ist.
# Signifikanztest für Korrelationskoeffizienten bestimmen
cor.test(data$J1, data$J2, use = "pairwise.complete.obs",
method = c("pearson", "kendall", "spearman"))##
## Pearson's product-moment correlation
##
## data: data$J1 and data$J2
## t = 3.1109, df = 4, p-value = 0.03584
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.09326324 0.98221144
## sample estimates:
## cor
## 0.8411582## J1 J2 J3 J4 J5 J6 J7 J8 J9
## J1 1.00 0.84 0.22 0.31 -0.05 0.22 0.45 0.31 0.31
## J2 0.84 1.00 0.15 0.14 0.00 0.15 0.28 0.14 0.14
## J3 0.22 0.15 1.00 0.97 0.94 1.00 0.95 0.97 0.97
## J4 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00
## J5 -0.05 0.00 0.94 0.89 1.00 0.94 0.78 0.89 0.89
## J6 0.22 0.15 1.00 0.97 0.94 1.00 0.95 0.97 0.97
## J7 0.45 0.28 0.95 0.94 0.78 0.95 1.00 0.94 0.94
## J8 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00
## J9 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00Nach Cohen (1988) wird die Stärke von Korrelationen bezeichnet als:
Geringe Korrelation: \(r = 0.10\) bis \(0.29\)
Mittlere Korrelation: \(r = 0.30\) bis \(0.49\)
Starke Korrelation: \(r \geq 0.50\)
Nur erwähnt sei an dieser Stelle, dass auch andere spezifische Zusammenhangsmaße existieren. Partialkorrelationen sind eine spezifische Form, bei welcher der Zusammenhang zwischen einem Variablenpaar durch das Auspartialisieren des Einflusses von Drittvariablen, z.B. mit der ‘R’-Programm-Bibliothek ‘ppcor’ (Kim, 2015), bestimmt wird. Wir werden später darauf zurückkommen.
## Loading required package: MASS## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1.00 -0.07 0.67 -0.62 0.09 0.67 0.46 -0.62 -0.62
## [2,] -0.07 1.00 -0.25 0.27 -0.82 -0.25 0.30 0.27 0.27
## [3,] 0.67 -0.25 1.00 0.96 0.04 -1.00 -0.80 0.96 0.96
## [4,] -0.62 0.27 0.96 1.00 -0.07 0.96 0.79 -1.00 -1.00
## [5,] 0.09 -0.82 0.04 -0.07 1.00 0.04 0.63 -0.07 -0.07
## [6,] 0.67 -0.25 -1.00 0.96 0.04 1.00 -0.80 0.96 0.96
## [7,] 0.46 0.30 -0.80 0.79 0.63 -0.80 1.00 0.79 0.79
## [8,] -0.62 0.27 0.96 -1.00 -0.07 0.96 0.79 1.00 -1.00
## [9,] -0.62 0.27 0.96 -1.00 -0.07 0.96 0.79 -1.00 1.005.6 Einfache (univariate) Regressions
Zunächst möchte ich auf eine Methode für den Nachweis von Zusammenhängen, Prognosen und Ursache-Wirkungs-Beziehungen (Kausalzusammenhängen) eingehen. Die Regressionsanalyse zählt zu den häufigsten statistischen Anwendungen, um Zusammenhänge zwischen metrischen (idealerweise intervallskalierten) Variablen zu beschreiben und zu prüfen. Üblicherweise wird dabei versucht, die unterschiedlichen Ausprägungen einer Variablen (meist als abhängige Variable bezeichnet) durch eine oder mehrere andere Variablen zu erklären (Dolic, 2010). Die abhängige Variable Y wird also als mathematische Funktion von X angesehen.
\[Y=f(X)\] Folgt man dabei der Annahme, dass die Beziehung zwischen X und Y deterministisch ist, kann diese Beziehung durch die allgemeine mathematische Gleichung: \[y=a + b \cdot x\] beschrieben werden (Bortz, 1993, S. 157). Durch diese lineare Gleichung ergibt sich jeder Wert der abhängigen Variable Y aus der Summe von a (dem Schnittpunkt der Geraden mit der y-Achse) und dem Produkt des Steigungskoeffizienten b mit dem Wert der unabhängigen Variable X (Bortz, 1993, S. 157).
Mit anderen Worten: durch das Wissen um a und b und die Funktionsgleichung kann für beliebige Werte x ein korrespondierendes y berechnet werden. Der Steigungskoeffizient b gibt darüber Auskunft, ob sich die ergebenden Werte in Y, bei ansteigenden Werten in X, vergrößern, verkleinern oder konstant bleiben.
## x y
## [1,] 0 2.5
## [2,] 1 3.0
## [3,] 2 3.5
## [4,] 3 4.0
## [5,] 4 4.5
## [6,] 5 5.0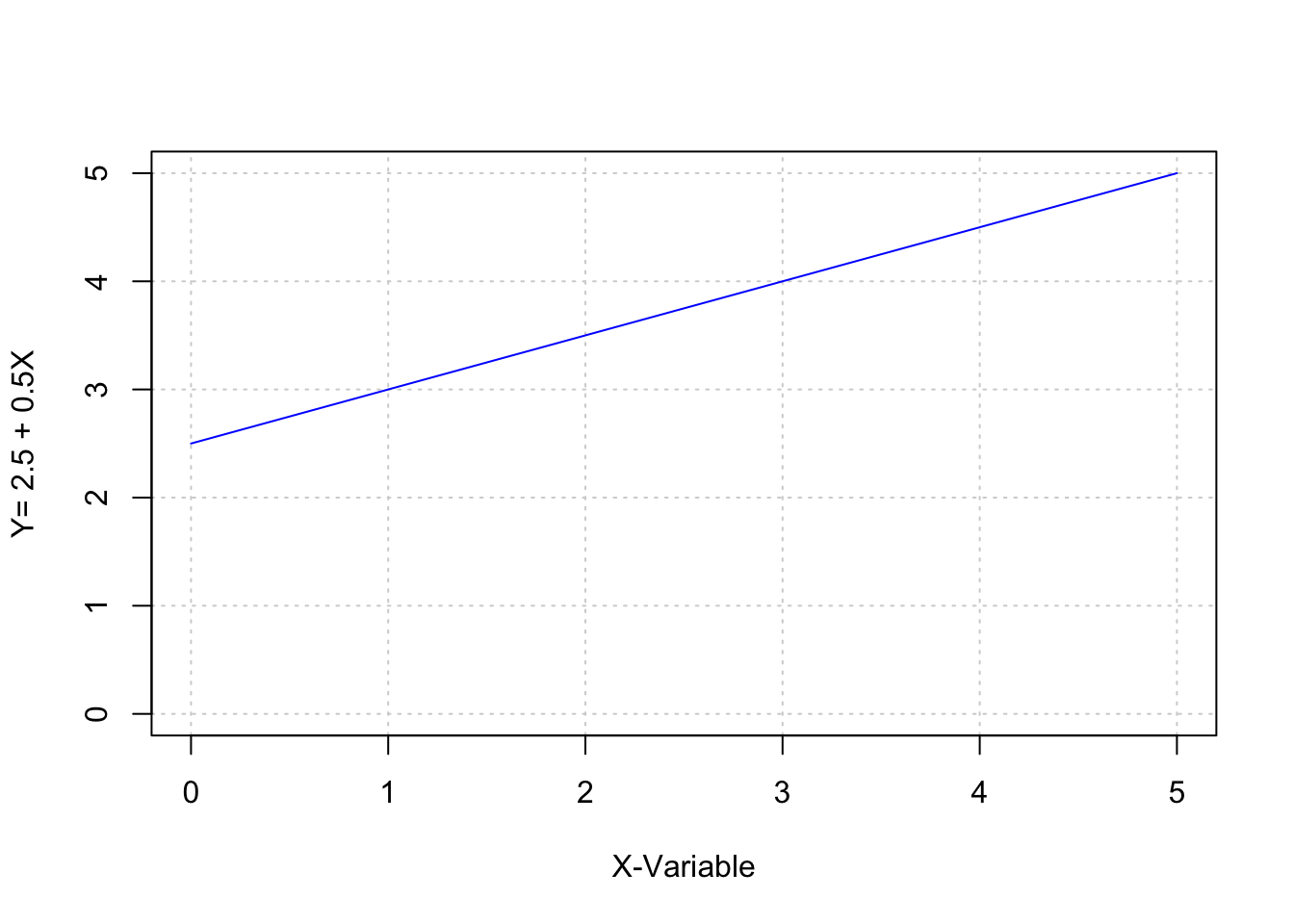
## x y
## [1,] 0 2.5
## [2,] 1 2.0
## [3,] 2 1.5
## [4,] 3 1.0
## [5,] 4 0.5
## [6,] 5 0.0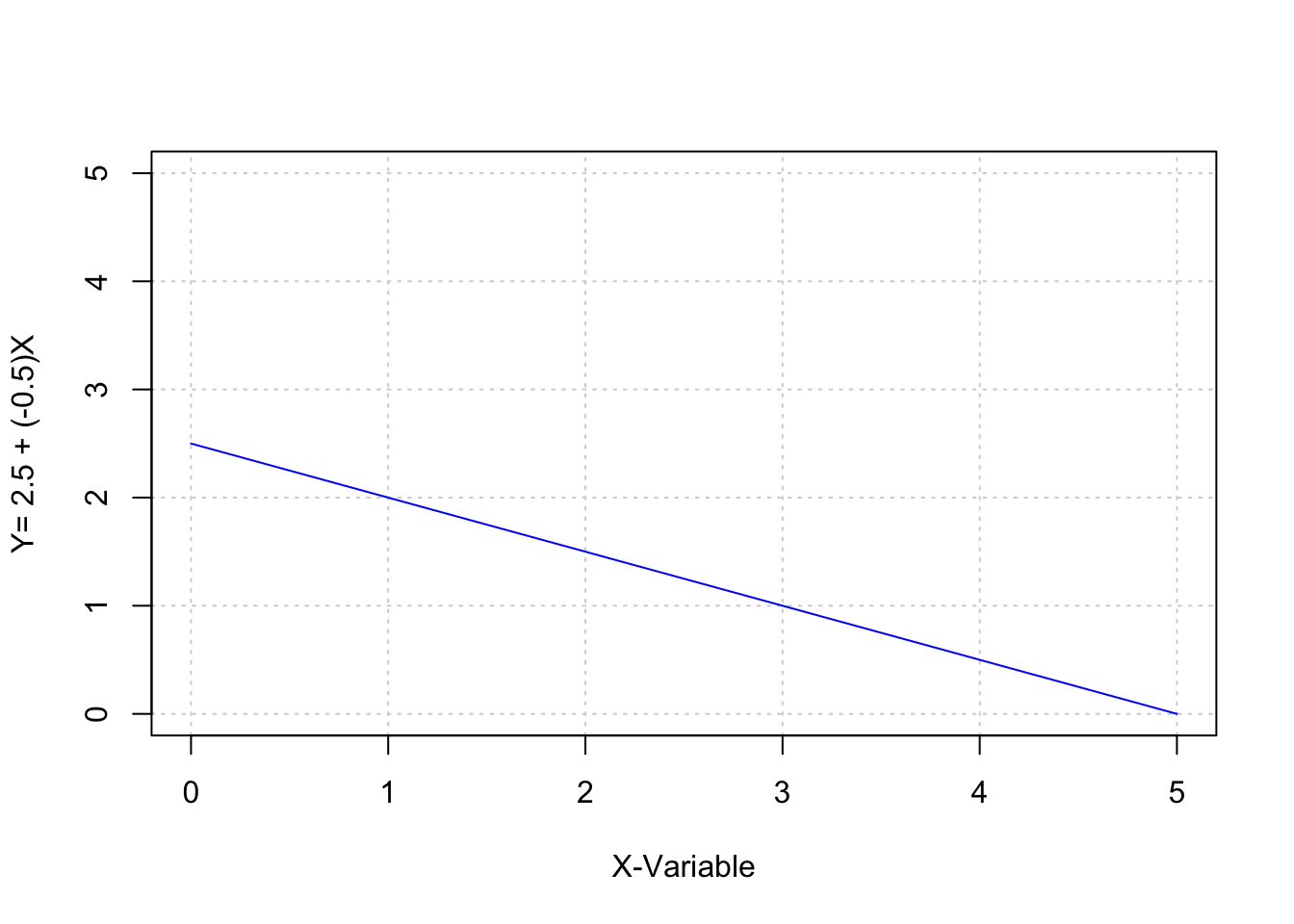
## x y
## [1,] 0 2.5
## [2,] 1 2.5
## [3,] 2 2.5
## [4,] 3 2.5
## [5,] 4 2.5
## [6,] 5 2.5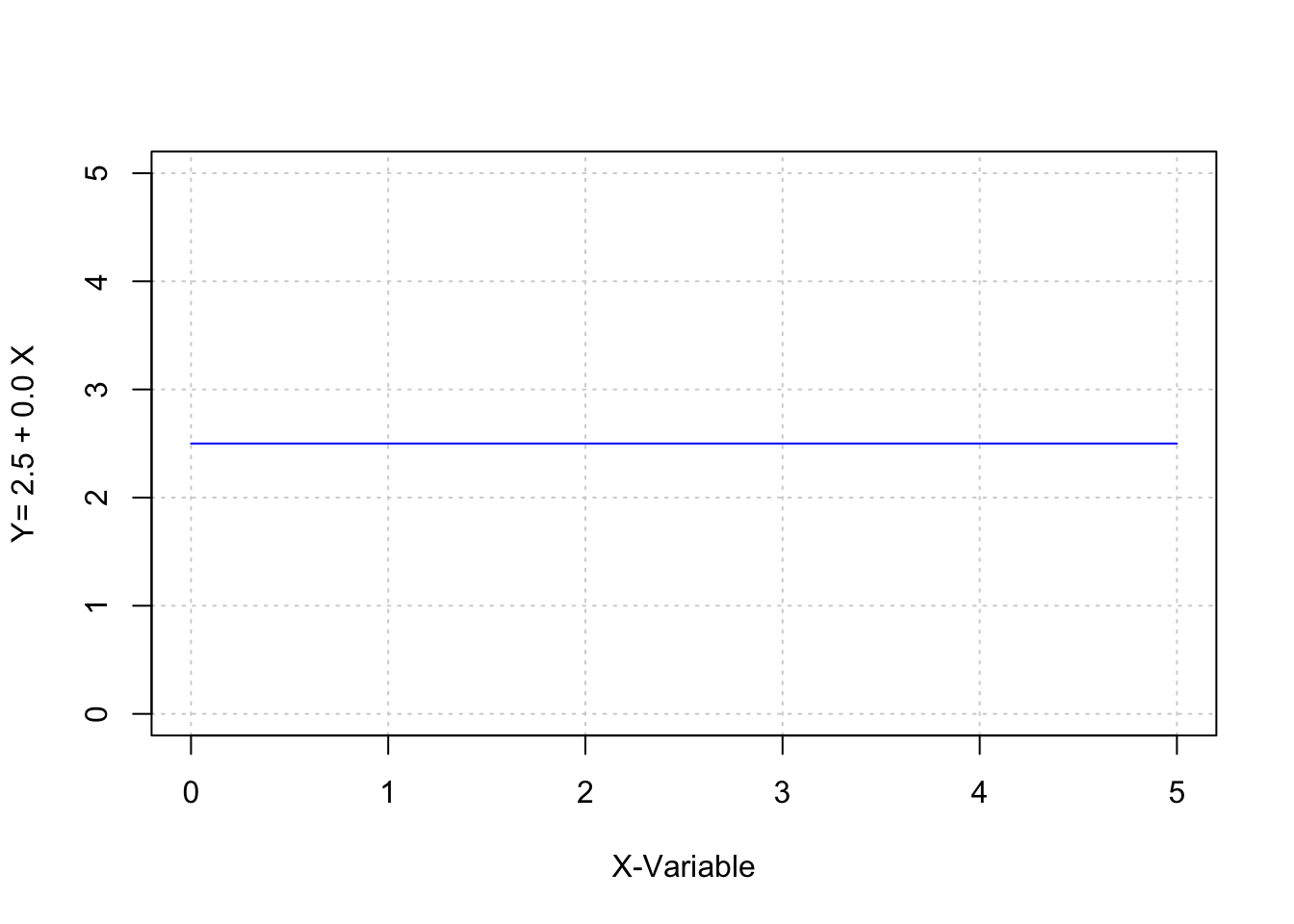
Da solche deterministischen Beziehungen in der Regel nicht der Realität entsprechen, wird die Regressionsgleichung (für die Beziehung zwischen zwei Variablen) um einen stochastischen Fehlerterm erweitert. In der einfachen Regression wird der Parameter \(\varepsilon\) verwendet. Als Residuum bezeichnet, bringt \(\varepsilon\)_ zum Ausdruck, dass die Variable Y neben der systematischen Beziehung zwischen X und Y auch “noch Variationen enthält, die nicht durch Variationen in der Variable X erklärbar sind” (Dolic, 2010, S. 214). \[ y_i=\alpha +\beta x_i + \varepsilon_i\] Das Residuum \(\varepsilon_i\) definiert sich als Differenz der prognostizierten (berechneten) und der realen (beobachteten) Werte der abhängigen Variablen:
\[\varepsilon_i= \hat{y_i}-y_i\]
Die Abbildung bildet neben dem deterministischen Zusammenhang, in dem die Variablen X per Definition über die Werte in Y bestimmt, auch einen vorstellbaren stochastischen Zusammenhang ab, indem das deterministische Modell durch einen normalverteilten Fehler erweitert wird.
## x y.d
## [1,] 1 1.5
## [2,] 2 2.5
## [3,] 3 3.5
## [4,] 4 4.5
## [5,] 5 5.5
## [6,] 6 6.5
## [7,] 7 7.5
## [8,] 8 8.5
## [9,] 9 9.5## x y
## [1,] 1 2.5 2.13 0.63
## [2,] 2 2.5 3.27 0.77
## [3,] 3 2.5 4.11 0.61
## [4,] 4 2.5 4.70 0.20
## [5,] 5 2.5 6.13 0.63
## [6,] 6 2.5 5.29 -1.21
## [7,] 7 2.5 9.54 2.04
## [8,] 8 2.5 9.04 0.54
## [9,] 9 2.5 9.75 0.25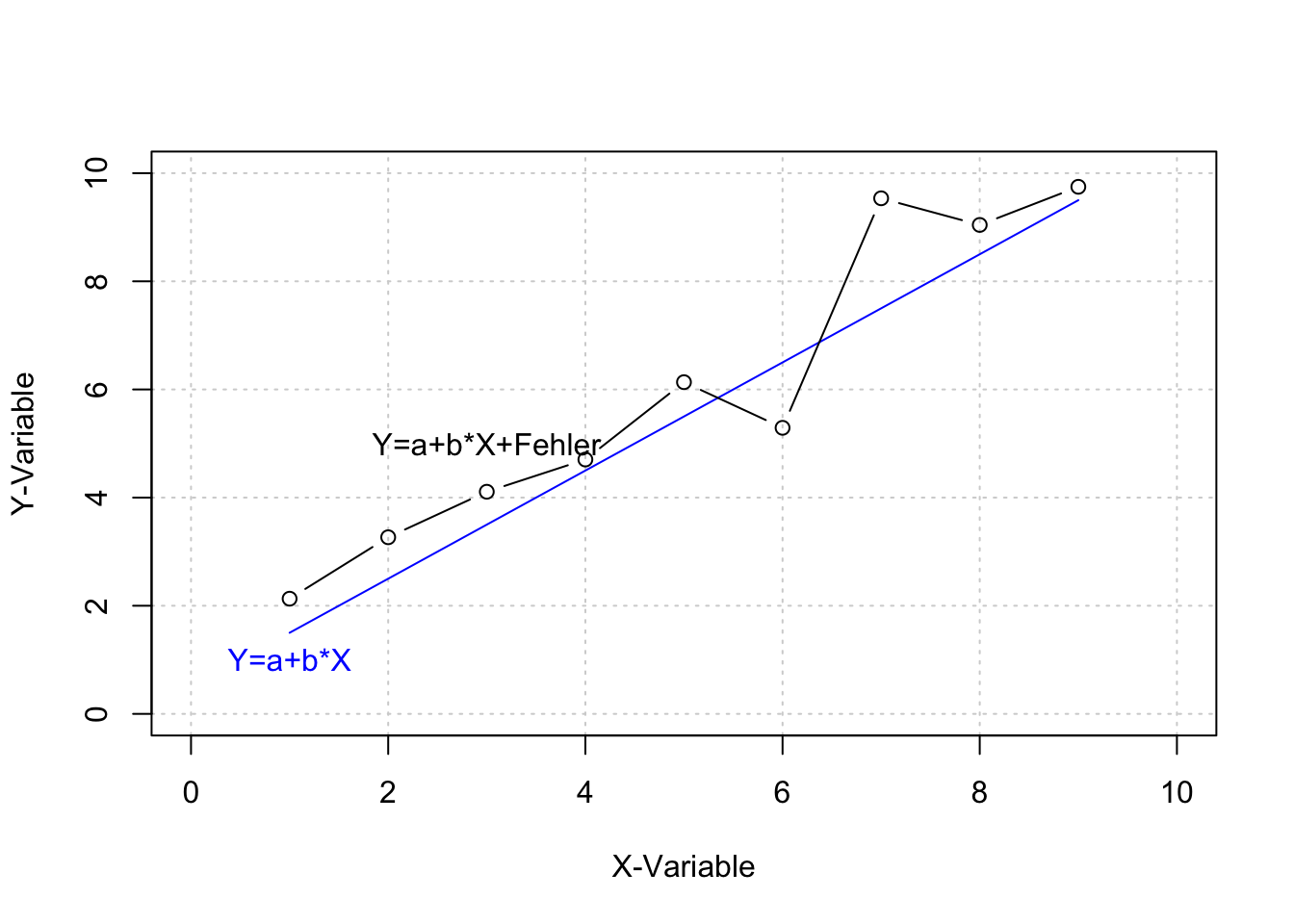
Die typische Forschungspraxis geht aber häufig in umgekehrter Weise vor. Aus den vorliegenden Werten für zwei Variablen wird eine lineare Gleichung abgeleitet. Dazu werden die Parameter a und b so gewählt werden, dass die Gleichung alle vorhandenen Variablenpaare möglichst präzise prognostizieren kann.
Die ideale Bestimmung der Parameter a und b liegt dann vor, wenn keine Abweichung zwischen den prognostizierten (berechneten) und den realen (beobachteten) Werten der Variable Y auftreten, d.h. wenn das Residuum \(\varepsilon_i\) für alle geschätzten \(\hat{y_i}\) gleich Null beträgt.
Weil dieses Ideal so unrealistisch wie deterministisch ist, wird nur die optimale Schätzgleichung bestimmt. Nach der Methode der kleinsten Quadrate (OLS), werden a und b so bestimmt, dass die Summe der quadrierten Residuen möglichst minimal wird:
\[\sum_{i=1}^n(\hat{y}-y_i)^2=min!\]
Statistiksoftware wie z.B. Excel, SPSS oder R bestimmen in ihrer Standardeinstellung nach dieser Methode und geben dem Nutzer im Ergebnis die Parameterschätzungen für a und b. Bezogen auf die oben beschriebenen Unterschiede zwischen dem deterministischen Zusammenhang \((y_d)\) und dem stochastischen Zusammenhang \((y_e)\) werden im Folgenden die Daten für beide Annahmen generiert. Die dann folgende lineare Regression (lm) bestimmt die Parameter für beide Regressionsmodelle.
## x y.d
## [1,] 1 1.5 2.13 0.63
## [2,] 2 2.5 3.27 0.77
## [3,] 3 3.5 4.11 0.61
## [4,] 4 4.5 4.70 0.20
## [5,] 5 5.5 6.13 0.63
## [6,] 6 6.5 5.29 -1.21
## [7,] 7 7.5 9.54 2.04
## [8,] 8 8.5 9.04 0.54
## [9,] 9 9.5 9.75 0.25Im Fall des deterministischen Zusammenhangs zwischen \(x\) und \(y_d\) wird das lineare Regressionsmodell immer das folgende Ergebnis aufzeigen:
##
## Call:
## lm(formula = y.d ~ x)
##
## Coefficients:
## (Intercept) x
## 0.5 1.0Die lineare Regression nach der Methode der kleinsten Quadrate ergibt einen Wert von 0.5 für a und einen Wert von 1.0 für b. Damit wurden exakt die Parameter bestimmt, nach denen die Werte generiert wurden.
Für den zweiten Fall (die Regression mit Daten, die einen stochastischen Zusammenhang darstellen sollen) werden abweichende Parameter a und b bestimmt.
##
## Call:
## lm(formula = y.e ~ x)
##
## Coefficients:
## (Intercept) x
## 1.0588 0.9873Damit wird nichts anderes aufgezeigt, als dass der in \(y_e\) enthaltene Fehler zu einer abweichenden Bestimmung von a und b führt. Um zu bestimmen, wie stark die Varianz in Y durch X verändert wird, wird eine sogenannte Varianzzerlegung vorgenommen und in Form des Determinationskoeffizienten \(R^2\) (auch Bestimmtheitsmaß genannt) angeboten.
Dieser Wert stellt die durch die Varianz in X erklärbare Varianz von Y in Relation zu der gesamten Varianz von Y. Ein kleiner Determinationskoeffizient (\(R^2\) ≤0.1) zeigt an, dass die Varianz der abhängigen Variable Y nur zu einem sehr geringen Teil (10 Prozent) durch die Varianz der unabhängigen Variablen X erklärt werden kann.
Neben dem Determinationskoeffizienten existieren weitere relevante Parameter der Modell-Statistik. Entscheidend für die Hypothesentestung ist der Steigungskoeffizient b bzw. seine standardisierte Form \(\beta\). Der (unstandardisierte) Steigungskoeffizient kann, je nach Skalenlänge der Variablen, einen Wertebereich von -\(\infty\) < b < +\(\infty\) annehmen. Mit einem negativen Wert für b wäre die inhaltliche Aussage assoziiert, dass größere Werte in X mit kleineren Werten in Y korrespondieren. Umgekehrt werden positive Werte für b mit einem positiven Zusammenhang von X auf Y dargestellt.
Typischerweise soll eine solche Aussage (Hypothese) hinsichtlich ihrer Signifikanz interpretiert werden. Der Parameter b wird dabei in Hinsicht auf die Nullhypothese (b=0) getestet. Aus b und seinem Standardfehler (b) wird die Prüfgröße bestimmt (t-Wert) und der in der t-Verteilung korrespondierende p-Wert ermittelt. Ist der p-Wert ≤ 0.05, wird die Nullhypothese verworfen (siehe auch Hypothesentestung). Ein insignifikanter p-Wert verweist inhaltlich auf die Annahme, dass in der Population b=0 ist.
##
## Call:
## lm(formula = y.e ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.69237 -0.19696 0.08508 0.13918 1.56501
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0588 0.6463 1.638 0.145
## x 0.9873 0.1149 8.597 5.74e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8896 on 7 degrees of freedom
## Multiple R-squared: 0.9135, Adjusted R-squared: 0.9011
## F-statistic: 73.9 on 1 and 7 DF, p-value: 5.742e-05In den bisherigen Ausführungen besteht kein Zweifel über die Unterscheidung von unabhängiger und abhängiger Variablen. Die Werte wurden für X spezifiziert und korrespondierende Werte für Y berechnet. Dabei wird die Manipulation der unabhängigen Variablen simuliert, so dass die abhängige Variable (wie in einem experimentellen Forschungsdesign) als Konsequenz der Manipulation von X angesehen werden kann. Wenn nur unzureichende Informationen über die kausale Wirkungsrichtung zwischen Variablen bestehen, muss der Forschende zunächst Aussagen auf Grundlage der Kovarianz der Variablen treffen.
set.seed(1975)
# normalverteilte Zufallswerte für X mit einem Mittelwert von 2.5
x <- 2.5+rnorm (1000)
a <- 0.5
b <- 1
# Deterministischer Zusammenhang
y.d <- a+b*x
# Stochastischer Zusammenhang
e <- rnorm(1000)/2 #normalverteilte Zufallswerte für 'e'
# Stochastischer Zusammenhang
y.e <- a+b*x+e
data <- as.data.frame(cbind(x, y.d, y.e, e))
plot(x,y.e,xlim=c(1,5),ylim=c(1,5),
xlab="X-Variable",ylab="Y (stochastisch)",
panel.first=grid(), col="blue")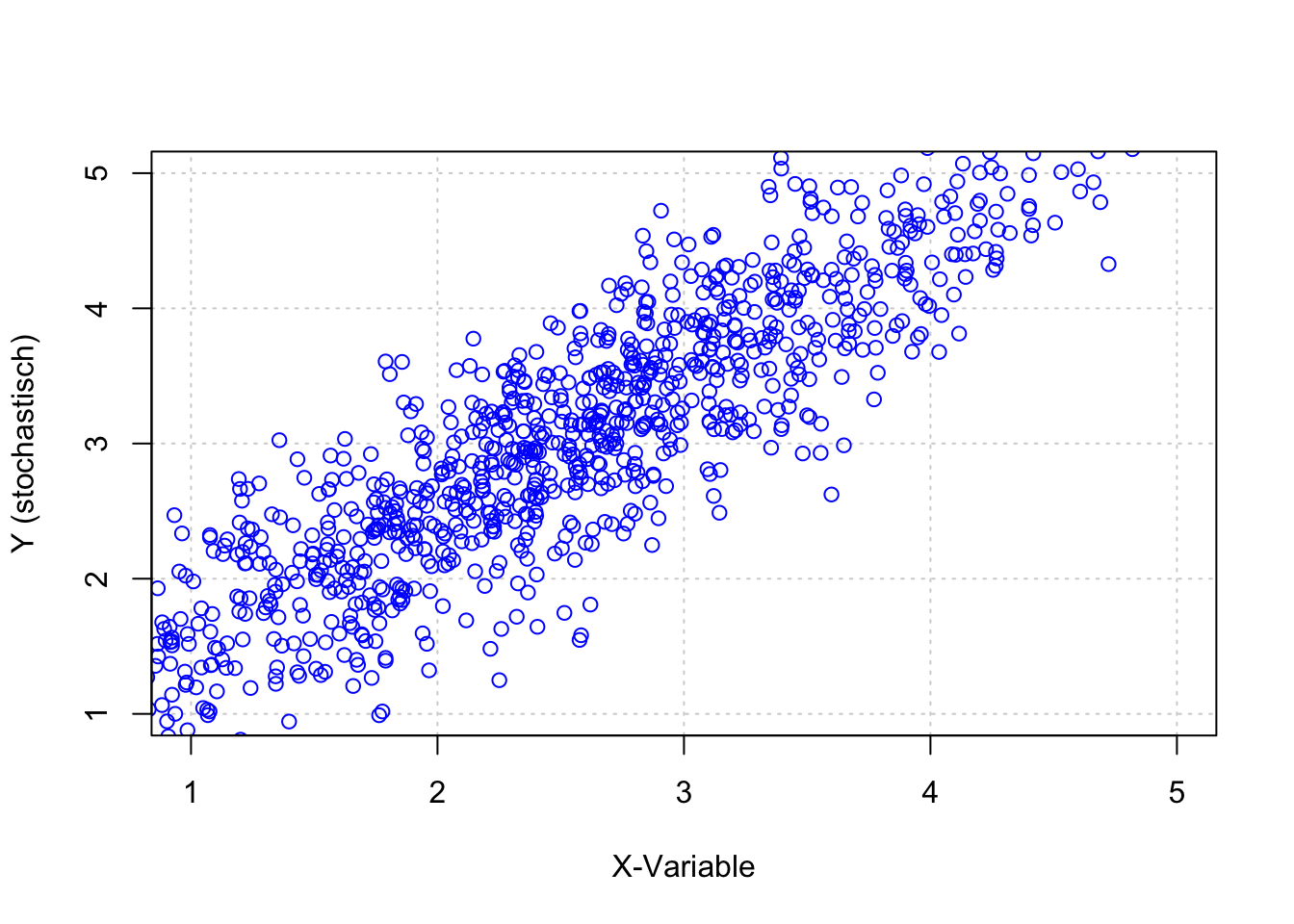
## [1] 1.058476Das Beispiel verdeutlicht, dass zwischen den Variablen \(X\) und \(Y_e\) eine Kovarianz von etwa \(cov(x, y_e)=1.04\) besteht. Inhaltlich bedeutet dies, dass bei einem Wertzuwachs von \(X\) in Höhe von Eins, ein durchschnittlicher Wertzuwachs in \(Y_e\) in Höhe von 1.06 zu erwarten ist. Es lässt ebenso die Aussage zu, dass mit bei einem Wertzuwachs von \(Y_e\) in Höhe von Eins ein durchschnittlicher Wertzuwachs in \(X\) in Höhe von 1.06 zu erwarten ist.
Aus den getroffenen Annahmen wissen wir, dass die Variationen in X als Ausgangspunkt für Variationen in Y angesehen werden können. Daher kann der Zusammenhang auch als Regression aufgefasst werden. Die \(cov(x,y)\) kann als Regression dargestellt werden, indem der Quotient der \(cov(x,y)\) und der Varianz in X, im Folgenden als \(var(x)\) dargestellt, bestimmt wird (Kenny, 2004, S. 23):
\[b_{YX}=\frac{cov(x,y)}{var(x)}\]
Die Varianz von x wird in R bestimmt durch die Anweisung:
## [1] 1.056424So kann der Regressionskoeffizient b, für die Annahme, dass \(X\) die unabhängige und \(Y_e\) die abhängige Variable ist, bestimmt werden aus:
# Bestimmen des Regressionskoeffizienten b für die Annahme,
# dass X die unabhängige und Ye die abhängige Variable ist.
cov(x, y.e)/ var(x)## [1] 1.001942Damit ist das Ergebnis identisch mit dem Steigungskoeffizienten b aus dem linearen Regressionsmodell.
##
## Call:
## lm(formula = y.e ~ x)
##
## Coefficients:
## (Intercept) x
## 0.5027 1.0019Zusammenfassend gibt diese Darstellung einen groben Überblick auf die traditionelle Funktionsweise der einfachen linearen Regression. Bei der Ableitung der Fehlerfunktion zur Minimierung der Residuen hatte ich die mathematische Herleitung nicht konsequent zu Ende weiterverfolgt.
Weil dieser Punkt für weitere Betrachtungen wichtig werden kann, sei hier noch einmal darauf eingegangen. Die Summe der quadrierten Fehler ist also gleich den quadrierten Residuen, die als Differenz der mittels Regressionsgleichung geschätzten \(\hat{y_i}\) und der (wahren) Werte \(y_i\) definiert sind.
\[\sum_{i=1}^{n}(\hat{y_i}-y_i)^2 = \sum_{i=1}^{n}((\alpha+\beta x_i)-y_i)^2=min!\]
Gesucht wird hier also eine Funktion für die Parameter \(f(\alpha,\beta)\). Diese kann mathematisch bestimmt werden, indem das im Gleichungssystem aufgelöst wird, nach \(\alpha\) und \(\beta\) umgestellt und die Ableitungen gleich Null gesetzt werden.
Die Existenz eines lokalen Extremwertes wird dann durch die Bildung der ersten und zweiten Ableitung geprüft. Im Resultat ergibt sich: \(\alpha=\overline{y}-\beta \: \overline{x}\) und nach zahlreichen weiteren Umformungen:
\[ \beta= \frac {\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^{n}(x_i-\overline{x})^2}= \frac{cov(x,y)}{var(x)}\]
Eine ausführlichere Herleitung zeigt beispielsweise Dolic (2010, S. 216–217).
5.7 Multiple (multivariate) Regression
Der Einsatz von Regressionsverfahren wird jedoch praktisch in den seltensten Fällen mit nur einer unabhängigen Variablen durchgeführt. Wird die im Modell zu bestimmende Regressionsgleichung um eine zweite unabhängige Variable z erweitert, ergibt sich die Funktion:
\[ y_i=\beta_0 + \beta_1 x_i + \beta_2 z_i + e_i \]
Aus einem solchen multiplen Regressionsmodell (mit zwei unabhängigen Variablen: x und z) können “Aussagen über den gleichzeitigen Einfluss mehrerer unabhängiger Variablen auf eine zu erklärende Variable” getroffen werden (Dolic, 2010, S. 220).
Das Modell erfordert jedoch spezifische Voraussetzungen, deren Verletzung zu einer verzerrten oder inkonsistenten Schätzung der Regressionsparameter führen kann (ebenda) und worauf wir später noch zu sprechen kommen werden.
Der Parameter b (der Steigungskoeffizient in der einfachen Regression) wird in der multiplen Regression durch mehrere (in diesem Beispiel durch zwei) unabhängige Variablen bestimmt. Die resultierenden Parameter \(\beta\) werden daher in der Regel mit fortlaufenden Nummern versehen.
In diesem Fall bestimmt \(\beta_1\) , um welchen Wert sich die abhängige Variable verändert, wenn x um den Wert von 1 zunimmt und \(\beta_2\) bestimmt, um welchen Wert sich die abhängige Variable verändert, wenn z um einen Wert von 1 zunimmt. Außerdem wird in der Gleichung für das multiple Regressionsmodell der Parameter a (der Schnittpunkt der Geraden mit der y-Achse) als \(\beta_0\) bezeichnet. An seiner Interpretation ändert sich nichts.
Das Residuum \(\varepsilon_i\) in der einfachen Regressionsgleichung wird durch den Fehlerterm \(e_i\) ersetzt. Diese Unterscheidung soll darauf hinweisen, dass der Fehlerterm (disturbance term) in dieser Funktion inhaltlich alle unberücksichtigten Quellen für Variationen in Y sowie jeder anderen Fehlerquelle (z.B. Messfehler) einschließt. In diesem Sinn unterscheidet sich das Residuum \(\varepsilon_i\) vom Fehlerterm \(e_i\) (Antonakis, Bendahan, Jacquart & Lalive, 2014, S. 14).
Sowohl die Bestimmung mittels Statistikprogrammen als auch die Interpretation der Koeffizienten hinsichtlich ihrer Signifikanz unterscheidet sich nicht von der einfachen Regression. Im Gegensatz zur einfachen Regression werden die Determinationskoeffizienten aber höher ausfallen, wenn Sie zwei geeignete unabhängige Variablen verwenden.
5.8 Additive Effekte
Wenn in einer Regressionsgleichung zwei oder mehr Variablen berücksichtigt werden, kann das Ergebnis Informationen über ihren additiven Effekt liefern. Additive Effekte bestimmen den Beitrag von zwei oder mehr unabhängigen Variablen auf eine abhängige Variable .
Beispiel: Ein Unternehmen möchte die Leistung beim Einsatz neuer Technologien verbessern und untersucht in diesem Zusammenhang die Anzahl der durchgeführten Schulungen und die Erfahrung der Mitarbeiter.
Im Folgenden ist die Leistung mit \(y\) bezeichnet und die Trainings (\(x\)) sowie die Erfahrung (\(z\)) in Matrixschreibweise dargestellt.
\[\begin{pmatrix} x_1 & z_1 \\ x_2 & z_2 \\ x_3 & z_3 \\ x_4 & z_4 \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}\]
Die einzelnen Zellen der \(x−z\) Matrix zeigen die möglichen Kombinationen von Trainings und Erfahrung, wobei eine 0 für “nicht zutreffend” und eine 1 für “zutreffend” steht. Die erste Zeile bezeichnet also die Situation, in der weder Training noch Erfahrung vorhanden sind.
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}\]
In der folgenden Abbildung wird der Zusammenhang zwischen Training und Leistung dargestellt. Mithilfe einer einfachen (univariaten) Regressionsanalyse wird der Einfluss der unabhängigen Variable Training auf die abhängige Variable Leistung untersucht.
set.seed(1899)
n=250
Training <- runif(n,1,5)
Erfahrung <- runif(n,1,5)
Motivation <- runif(n,1,5)
Kompetenz <- Training + Erfahrung + runif(n,-0.6,0.6)
Leistung <- Kompetenz + Motivation + runif(n,-0.6,0.6)
Fehler <- 15.6 - Leistung
plot (Training, Leistung, xlab="Anzahl durchgeführter Trainings", ylab= "Leistung im Einsatz neuer Technologien")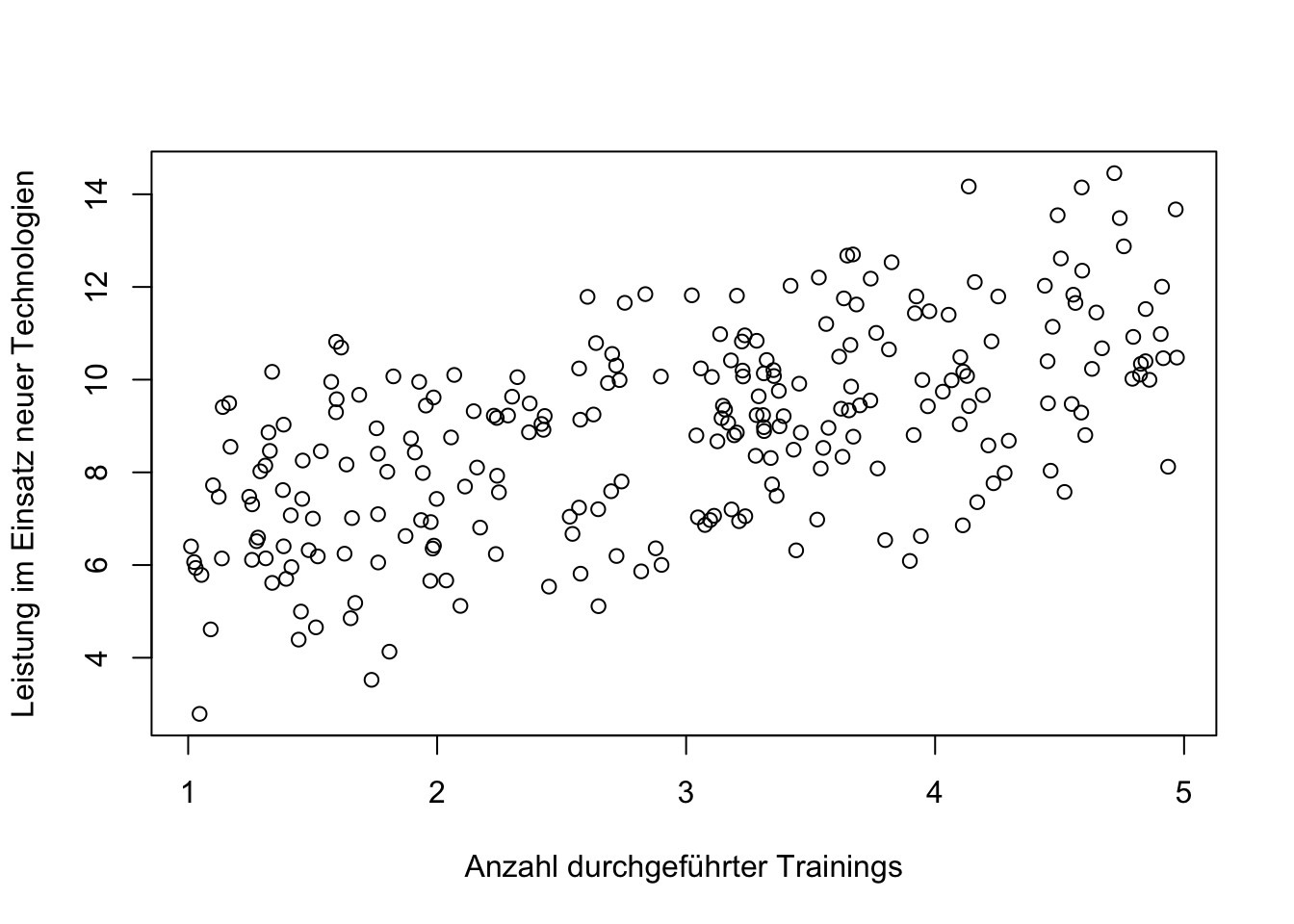
##
## Call:
## lm(formula = Leistung ~ Training)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0194 -1.1398 -0.0913 1.2516 3.9406
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.59941 0.30392 18.42 <2e-16 ***
## Training 1.11906 0.09634 11.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.728 on 248 degrees of freedom
## Multiple R-squared: 0.3523, Adjusted R-squared: 0.3497
## F-statistic: 134.9 on 1 and 248 DF, p-value: < 2.2e-16Das Ergebniss zeigt, dass Trainings in einem signifikant positiven Zusammenhang mit Leistung stehen. Das Modell erklärt 35 Prozent der Varianz in der Leistung.
Im nächsten Modell wird der Zusammenhang zwischen der Erfahrung der Mitarbeiter und der Leistung dargestellt.
plot (Erfahrung, Leistung, xlab="Erfahrung des Mitarbeiters", ylab= "Leistung im Einsatz neuer Technologien")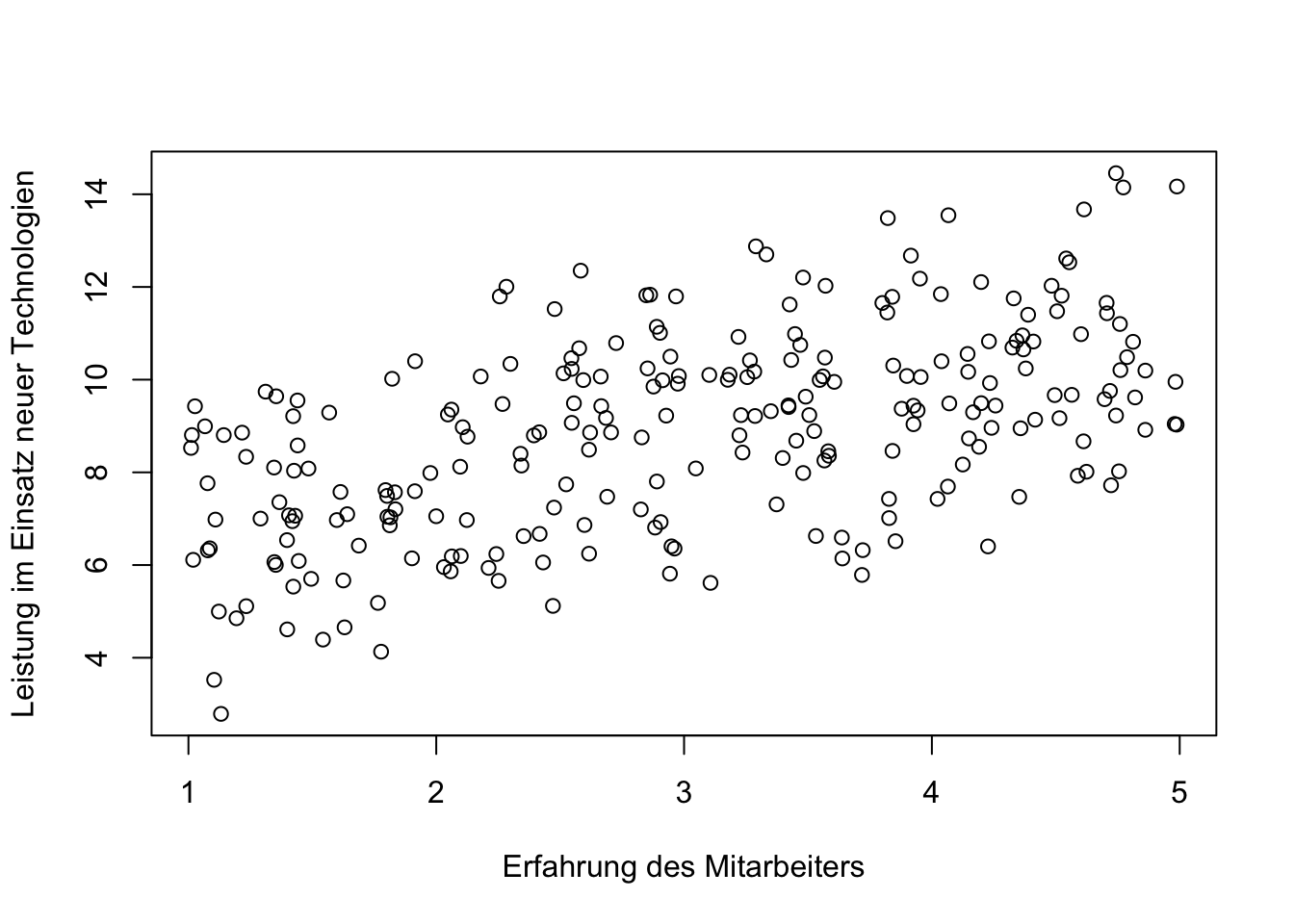
##
## Call:
## lm(formula = Leistung ~ Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2105 -1.2355 0.0242 1.2688 3.8902
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.8596 0.3196 18.34 <2e-16 ***
## Erfahrung 1.0073 0.0991 10.16 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.804 on 248 degrees of freedom
## Multiple R-squared: 0.2941, Adjusted R-squared: 0.2912
## F-statistic: 103.3 on 1 and 248 DF, p-value: < 2.2e-16Auch hier wird ein signifikant positiver Zusammenhang aufgezeigt, der 30 Prozent \(R^2=0.29\) in der Varianz der Leistung erklärt.
Als drittes Modell wird hier das multivariate Regressionsmodell mit Trainings und Erfahrung dargestellt. Es bestätigt die positiven Zusammenhänge zwischen Trainings und Leistung sowie zwischen Erfahrung und Leistung.
##
## Call:
## lm(formula = Leistung ~ Training + Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.73051 -1.02372 -0.07258 1.00113 3.00571
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.40800 0.30534 7.886 1e-13 ***
## Training 1.14456 0.06972 16.417 <2e-16 ***
## Erfahrung 1.03465 0.06869 15.063 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.25 on 247 degrees of freedom
## Multiple R-squared: 0.6624, Adjusted R-squared: 0.6597
## F-statistic: 242.3 on 2 and 247 DF, p-value: < 2.2e-16Der additive Effekt von Trainings und Erfahrung wird aus der Tatsache deutlich, dass mit dem multivariaten Regressionsmodell 66 Prozent in der Varianz von Leistung erklärt werden können \((R^2=0.66)\).
Additive Modelle sind geeignet für Fragestellungen, bei denen der Einfluss mehrerer Variablen auf eine abhängige Variable untersucht wird. Die “erklärenden” Variablen sollten verschiedene Aspekte darstellen, die unabhängig voneinander sind.
Gelegentlich werden Aspekte wie Erfahrung und Training als Supplemente bezeichnet, d.h. sie bieten Ergänzungen in der Erklärung von Leistung.
Hohe korrelative Zusammenhänge zwischen den unabhängigen Variablen können die Schätzungen der Regressionskoeffizienten beeinflussen, was Auswirkungen auf deren Genauigkeit und Interpretation hat.
Das Ziel eines additiven Regressionsmodells besteht darin, den Erklärungsgehalt zu erhöhen, was sich in einem höheren Determinationskoeffizienten \(R^2\) zeigt.
Schließlich wird hier gezeigt, wie sich die Trainings und die Erfahrung der Mitarbeiter auf die Häufigkeit von Fehlern im Einsatz neuer Technologien auswirken.
par(mfrow=c(1,2))
plot (Training, Fehler, xlab="Anzahl durchgeführter Trainings", ylab= "Fehler im Einsatz neuer Technologien")
plot (Erfahrung, Fehler, xlab="Erfahrung des Mitarbeiters", ylab= "Fehler im Einsatz neuer Technologien")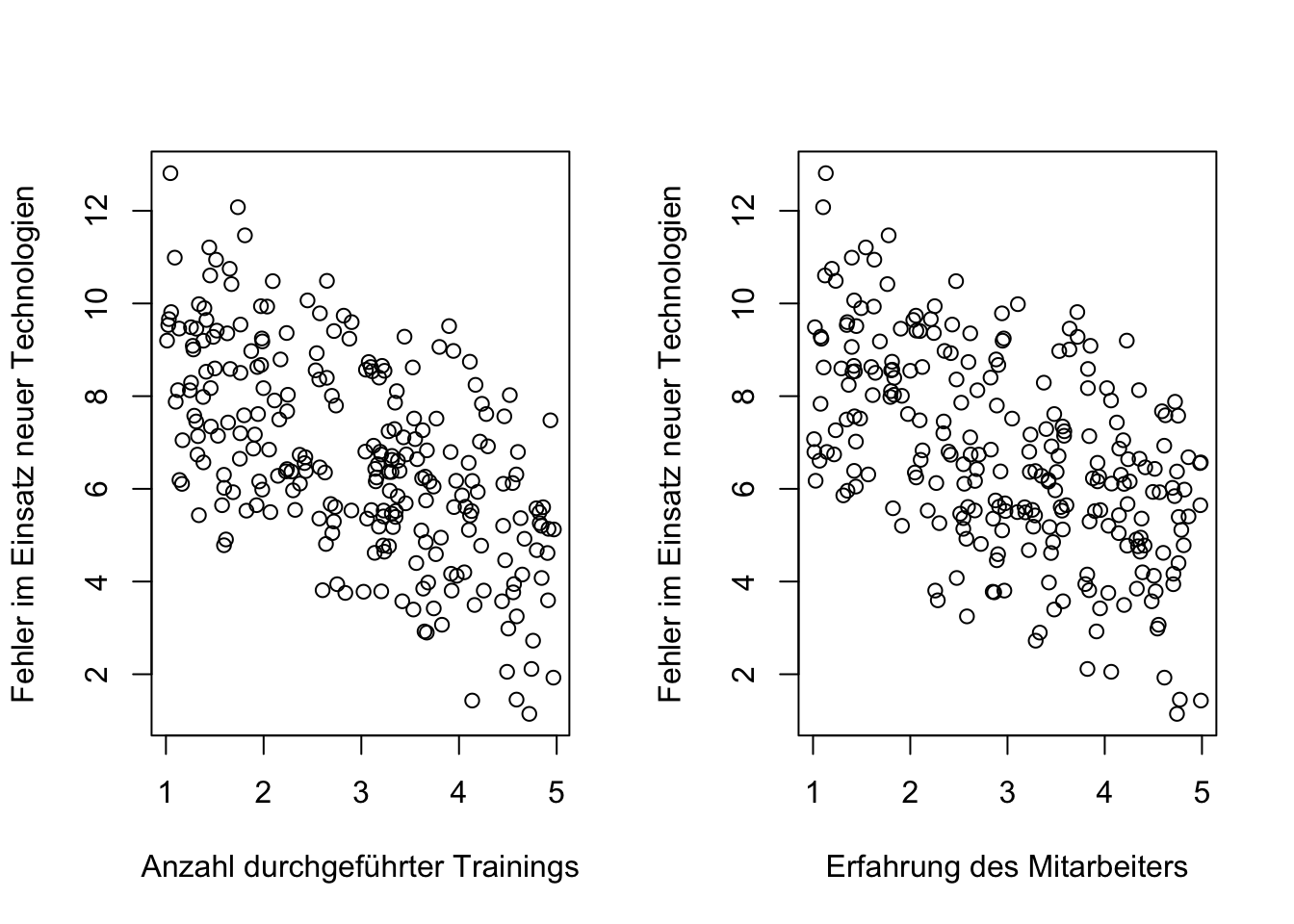
##
## Call:
## lm(formula = Fehler ~ Training + Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.00571 -1.00113 0.07258 1.02372 2.73051
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.19200 0.30534 43.20 <2e-16 ***
## Training -1.14456 0.06972 -16.42 <2e-16 ***
## Erfahrung -1.03465 0.06869 -15.06 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.25 on 247 degrees of freedom
## Multiple R-squared: 0.6624, Adjusted R-squared: 0.6597
## F-statistic: 242.3 on 2 and 247 DF, p-value: < 2.2e-16Das Ergebnis der Regression deutet darauf hin, dass eine höhere Anzahl von Trainings und/oder Erfahrungen mit einer geringeren Fehlerquote verbunden sind. Auch in diesem Fall handelt es sich um einen additiven Effekt, da die beiden Aspekte (Erfahrung und/oder Training) additiv in der Regressionsgleichung kombiniert werden, um den Erklärungsgehalt des Modells zu verbessern. “Additiv” bezieht sich hier nicht auf die fördernde oder hemmende “Wirkung” der Variablen, sondern auf ihre mathematische Verknüpfung im Regressionsmodell.
5.9 Nicht additive Effekte
“Nonadditive effects signify that the combination of two or more variables does not produce an outcome that is the sum of their individual effects.” (Aiken & West, 2014, S. 3)
Es handelt sich hier also um Situationen, in denen die Kombination von zwei oder mehr Variablen nicht zu dem erwarteten Ergebnis führt, dass aus den individuellen Effekte zu erwarten ist.
5.9.1 Mediation
Das vorangegangenen Beispiel hat aufgezeigt, dass die Mitarbeiter mit häufigen Trainings und/ oder höheren Erfahrungen bessere Leistungen und weniger Fehler aufzeigen. Das multivariate Regressionsmodell zeigte signifikant positive Regressionskoeffizienten für beide Faktoren (Trainings und Erfahrungen). Insgesamt erklärte das Regressionsmodell 66 Prozent in der Varianz der Leistung.
Mit der Intention, die Leistung der Mitarbeiter noch genauer vorhersagen zu können, berücksichtigt ein Forscher zusätzlich Fähigkeiten, Kenntnisse oder Verhaltensweisen der Mitarbeiter, die hier umgangssprachlich als “Kompetenzen” bezeichnet werden.
Er erwartet, dass die positiven Effekte von Training und Erfahrungen durch den positiven Effekt von Kompetenz ergänzt werden und die Varianz der Leistung noch besser erklärt werden kann.
# Multivariates Modell erweitert um Kompetenz
summary (lm (Leistung ~ Training + Erfahrung + Kompetenz))##
## Call:
## lm(formula = Leistung ~ Training + Erfahrung + Kompetenz)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.43684 -0.97649 -0.07286 0.99935 2.30188
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.60039 0.28932 8.988 < 2e-16 ***
## Training -0.08363 0.22405 -0.373 0.709
## Erfahrung -0.23798 0.23120 -1.029 0.304
## Kompetenz 1.22158 0.21308 5.733 2.88e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.176 on 246 degrees of freedom
## Multiple R-squared: 0.7022, Adjusted R-squared: 0.6986
## F-statistic: 193.4 on 3 and 246 DF, p-value: < 2.2e-16Die Hinzunahme von Kompetenz in das Regressionsmodell ist in Hinsicht auf das \(R^2=0.95\) ein Erfolg.
Mit Erschrecken ist jedoch festzustellen, dass die Regressionskoeffizienten von Training und Erfahrung mit \(p≥ 0.05\) assoziiert sind. Warum liegt hier der bereits bestätigte Effekt nicht vor?
Trainings haben das Ziel, den Mitarbeitern neue Fähigkeiten, Kenntnisse oder Verhaltensweisen zu vermitteln, die hier als Kompetenzen bezeichnet wurden. Die Kompetenzen sind demnach nicht unabhängig von Trainings, vielmehr noch, sie sind Ergebnis aus den Trainings, bzw. ein “Meilenstein” zwischen Training und Leistung.
Diese Form der Verkettung von Eigenschaften, Ereignissen oder Prozessen wird als Mediation bezeichnet. Eine allgemeine Definition für die Mediation stammt von Baron & Kenny (1986, S. 1176):
„[Mediators are] entities or processes that intervene between input and output.“
Basierend auf dem, was ein Mitarbeiter in den Trainings lernt (z. B. Fakten, Konzepte, Prinzipien oder Verfahren), erwirbt er “Kompetenzen”, die wiederum zu einer besseren Leistung und weniger Fehlern beitragen.
Das Modell postuliert also, dass Trainings zu Kompetenzen führen und diese Kompetenzen eine bessere Leistung hervorbringen. Der Zusammenhang zwischen Trainings und Leistung wird demnach durch erworbene Kompetenzen vermittelt (mediert) oder, wie von Pearl (2009a) formuliert, sie bilden eine Kette (chain).
Die Ergebnisse eines solchen Modells könnten dahingehend interpretiert werden, dass eine Ursache für Leistung in den Kompetenzen liegt, die wiederum aus den Trainings resultieren.
Baron & Kenny (1986, S. 1177) schlagen einen analytischen Test vor, mit dem ein Mediator getestet werden kann. Hierfür werden nacheinander drei Regressionsmodelle überprüft.
Mediationsanalyse nach Baron & Kenny (1986)
- Bestimmung des Regressionskoeffizienten der unabhängigen Variablen (Trainings) auf den Mediator (Kompetenz) in einem univariaten Regressionsmodell
- Bestimmung des Regressionskoeffizienten der unabhängigen Variablen (Trainings) auf die abhängige Variable (Leistung) in einem univariaten Regressionsmodell
- Bestimmung der Regressionskoeffizienten der unabhängigen Variablen (Trainings) und des potenziellen Mediators (Kompetenz) auf die abhängige Variable (Leistung) in einem multivariaten Regressionsmodell
Damit eine Variable als Mediator in Betracht gezogen werden kann, müssen in Schritt 1 und 2 signifikante Regressionskoeffizienten festgestellt werden. In Schritt 3 sollte der Regressionskoeffizient des Mediators signifikant sein, während der Regressionskoeffizient der unabhängigen Variablen insignifikant sein sollte.
Es soll überprüft werden, ob der Zusammenhang zwischen Trainings und Leistung (\(\beta\)=1.12, t=11.62, p≤0.001) durch steigende Kompetenz erklärt werden kann.
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Erster Schritt
summary (lm (Kompetenz ~ Training))##
## Call:
## lm(formula = Kompetenz ~ Training)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.44606 -1.07390 0.07284 1.03895 2.35768
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.05595 0.22054 13.86 <2e-16 ***
## Training 0.97973 0.06991 14.01 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.254 on 248 degrees of freedom
## Multiple R-squared: 0.4419, Adjusted R-squared: 0.4397
## F-statistic: 196.4 on 1 and 248 DF, p-value: < 2.2e-16Der erste Schritt der Mediationsanalyse nach Baron & Kenny (1986) zeigt einen signifikant positiven Regressionskoeffizient von Trainings (\(\beta=0.98; t=14.01; p≤0.001\)) auf den Mediator Kompetenz (hier als abhängige Variable) auf.
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Zweiter Schritt
summary(lm(Leistung ~ Training))##
## Call:
## lm(formula = Leistung ~ Training)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0194 -1.1398 -0.0913 1.2516 3.9406
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.59941 0.30392 18.42 <2e-16 ***
## Training 1.11906 0.09634 11.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.728 on 248 degrees of freedom
## Multiple R-squared: 0.3523, Adjusted R-squared: 0.3497
## F-statistic: 134.9 on 1 and 248 DF, p-value: < 2.2e-16Der zweite Schritt der Mediationsanalyse zeigt einen signifikanten positiven Zusammenhang zwischen Training und Leistung auf (\(\beta\)=1.12, t=11.62, p≤0.001).
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Dritter Schritt
summary (lm (Leistung ~ Training + Kompetenz))##
## Call:
## lm(formula = Leistung ~ Training + Kompetenz)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.36247 -0.94722 -0.08235 0.98478 2.42623
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.50983 0.27565 9.105 <2e-16 ***
## Training 0.12855 0.08781 1.464 0.145
## Kompetenz 1.01100 0.05958 16.967 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.177 on 247 degrees of freedom
## Multiple R-squared: 0.7009, Adjusted R-squared: 0.6985
## F-statistic: 289.4 on 2 and 247 DF, p-value: < 2.2e-16Im dritten Schritt (der multiplen Regression) zeigt sich der Zusammenhang zwischen Trainings und Leistung unsignifikant (\(\beta\)=0.13, t=1.46, p=0.145) und es wird ein signifikant positiver Zusammenhang zwischen Kompetenz und Leistung (\(\beta\)=1.01, t=16.97, p≤0.001) aufgezeigt.
Im Sinne von Baron & Kenny (1986) kann Kompetenz folglich als Vermittler (Mediator) für den Zusammenhang zwischen Trainings und Leistung betrachtet werden.
Ein besonderer Fall tritt auf, wenn der Regressionskoeffizient der unabhängigen Variablen zwar noch signifikant ist, jedoch einen deutlich geringeren Wert aufweist. Dies wird als partielle Mediation bezeichnet. Weitere Untersuchungen, wie zum Beispiel der Sobel-Test, können dazu beitragen, das Ausmaß dieser partiellen Mediation klarer zu definieren.
Das Konzept der Mediation setzt eine einseitige Richtung zwischen den Variablen voraus, was als rekursives Modell beschrieben wird. In der Notation der konditionalen Unabhängigkeit wird die Mediation als ‘chain’ bezeichnet. Die damit verbundene Interpretationslogik findet auch Anwendung in weiteren Analyseverfahren, wie z. B. der Strukturgleichungsmodellierung. Dabei wird das Ergebnis in Gesamteffekte, direkte Effekte und indirekte Effekte (Kline, 2015; Muthén & Asparouhov, 2015) unterschieden.
Der Gesamteffekt einer unabhängigen Variablen auf die abhängige Variable ist die Summe des direkten Effekts und des totalen indirekten Effekts (Muthén, 2011):
\[ TE = DE + TIE \] Der totale indirekte Effekt einer unabhängigen Variable auf eine abhängige Variable ergibt sich aus dem Produkt der Koeffizienten aus dem Regressionsmodell der unabhängigen Variablen (X) auf den Mediator (M) aus Schritt 1 und dem Regressionskoeffizienten des Mediators (M) auf die abhängige Variable (Y) in Schritt 3.
\[ TIE = \gamma_{X|M} \cdot \beta_{M|Y}\]
Für das obige Beispiel ergibt sich somit ein indirekter Effekt (TIE) von Trainings auf Leistung aus dem Produkt der Koeffizienten aus Schritt 1 und Schritt 3 als: \[0.98 \cdot 1.01 = 0.99\]
Bei einem direkten Effekt in Höhe von 0.13 (Schritt 3) ergibt sich ein totaler Effekt von:
\[0.13 + 0.99 = 1.12\]
für den Zusammenhang zwischen Trainings und Leistung. Dies entspricht in etwa dem Koeffizienten aus Schritt 2 (univariates Modell).
Der indirekte Effekt macht somit etwa 90 Prozent des totalen Effektes von Training auf Leistung aus. Mit anderen Worten wird der Zusammenhang zwischen Training und Leistung in diesem Mediationsmodell zu etwa 90 Prozent durch Kompetenz erklärt.
5.9.2 Moderation
Eine weitere Form nicht additiver Effekte liegt vor, wenn Moderationen aufgezeigt werden. Eine allgemeine Definition stammt ebenfalls von Baron & Kenny (1986):
„In general terms, a moderator is a […] variable that effects the direction and/ or strenght of the relation between an independent or predictor variable and a dependent or criterion variable“.
Es handelt sich hier also nicht um den Effekt einer Ursache (effect of cause) sondern vielmehr um die Ursache eines Effektes (cause of effect).
Betrachten wir wieder das Beispiel mit Trainings und Kompetenz aus dem ersten Schritt der Mediatoranalyse.
##
## Call:
## lm(formula = Kompetenz ~ Training)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.44606 -1.07390 0.07284 1.03895 2.35768
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.05595 0.22054 13.86 <2e-16 ***
## Training 0.97973 0.06991 14.01 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.254 on 248 degrees of freedom
## Multiple R-squared: 0.4419, Adjusted R-squared: 0.4397
## F-statistic: 196.4 on 1 and 248 DF, p-value: < 2.2e-16Im diesem Beispiel gingen wir davon aus, das Erfahrung und Trainings unabhängige Zufallsvariablen sind. Im folgenden Beispiel berücksichtigen wir, dass diejenigen Mitarbeiter häufiger den Trainingsmaßnahmen zugeordnet werden, die nicht über ausreichende Erfahrungen verfügten. Die (mangelnde) Erfahrung ist demnach eine Ursache für die Trainings bzw. den Effekt, den wir von Training auf Kompetenz ausmachen können.
set.seed(1899)
Training <- runif(n,6-Erfahrung,5)
Kompetenz <- ifelse (Erfahrung > Training, Erfahrung + runif(n,-0.6,0.6), Training + runif(n,-0.6,0.6))
Leistung <- Kompetenz + Motivation + runif(n,-0.6,0.6)
Fehler <- 15.6 - Leistung
plot (Erfahrung, Training)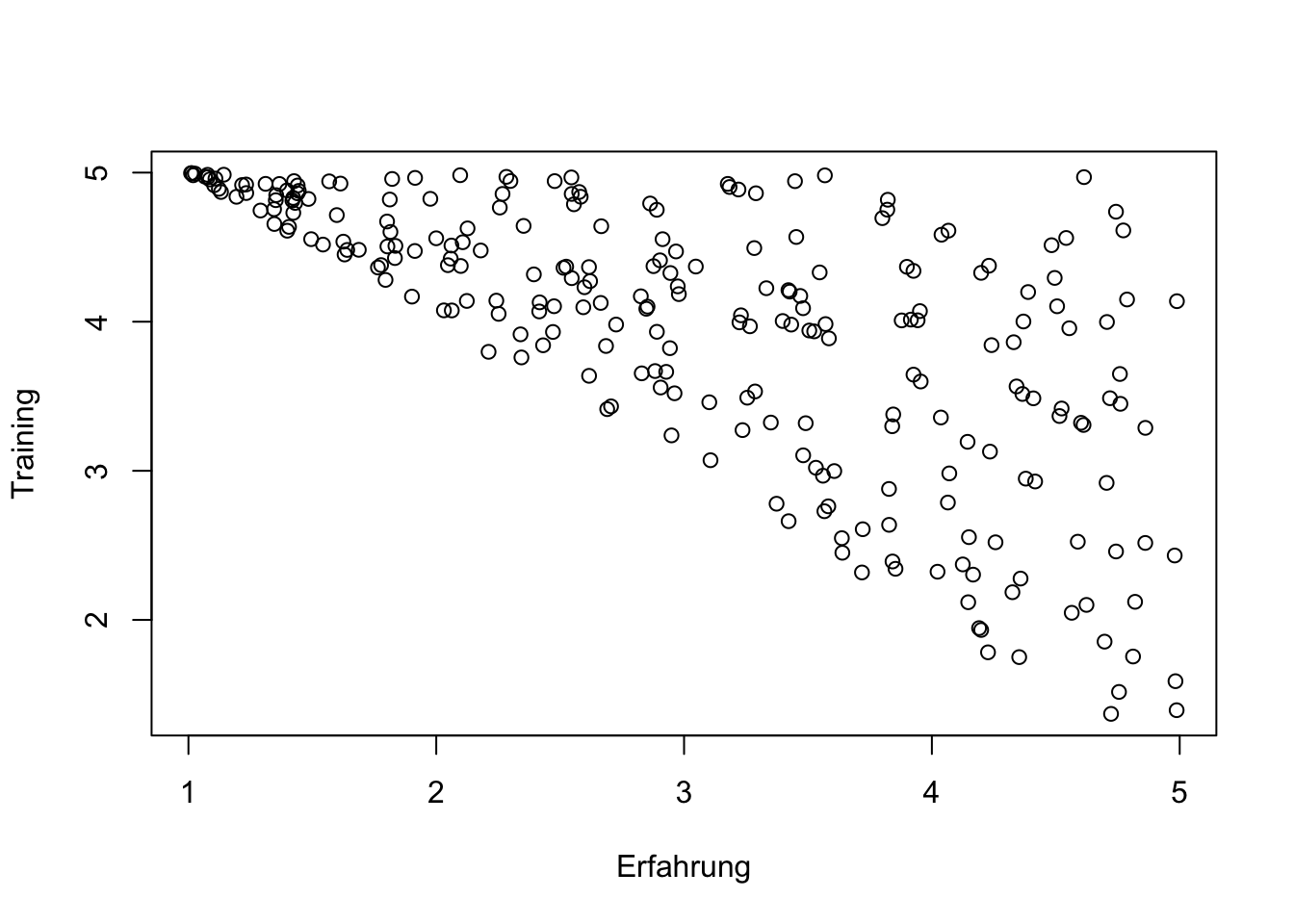
##
## Call:
## lm(formula = Kompetenz ~ Training)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.49379 -0.41896 0.01356 0.39653 1.30602
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.15753 0.16113 25.802 <2e-16 ***
## Training 0.08635 0.03969 2.176 0.0305 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5682 on 248 degrees of freedom
## Multiple R-squared: 0.01873, Adjusted R-squared: 0.01477
## F-statistic: 4.734 on 1 and 248 DF, p-value: 0.03052Die Erfahrung der Mitarbeiter bestimmt also die Stärke des Effektes von Training auf Kompetenz. Je geringer die Erfahrung umso stärker sollte der Effekt von Trainings auf die Kompetenz ausfallen.
Für die hier vorliegenden metrische Variablen schlagen Baron & Kenny (1986) einen analytischen Test vor, der den Produktterm der unabhängigen Variablen \(x\) und des Moderators \(z\) in die Regressionsgleichung einbezieht.
\[ y_i=\beta_0 + \beta_1 x_i + \beta_2 z_i + \beta_3x_iz_i+e_i \] Baron & Kenny (1986) argumentieren, dass ein Moderatoreffekt durch einen signifikanten Koeffizienten des Interaktionsterms angezeigt wird.
“So if the independent variable is denoted as X, the moderater as Z, and the dependent variable as Y, Y is regressed on X, Z, and XZ. Moderator effects are indicated by the significant effect of XZ while X and Z are controlled.” (Baron & Kenny, 1986, S. 1176)
Die Unterscheidung zwischen unabhängiger Variable bzw. Moderator wird in dieser Gleichung analytisch nicht berücksichtigt. Daher wird dieses Vorgehen häufig verallgemeinert als Interaktionsanalyse bezeichnet (Berry, Golder & Milton, 2012) oder die Zuweisung des Moderators ist theoretisch herzuleiten (Baron & Kenny, 1986).
Training_Erfahrung = Training * Erfahrung
summary (lm (Kompetenz ~ Training + Erfahrung + Training_Erfahrung))##
## Call:
## lm(formula = Kompetenz ~ Training + Erfahrung + Training_Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.85963 -0.20336 0.03828 0.18249 0.81553
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.26598 0.52833 -13.75 <2e-16 ***
## Training 2.50499 0.11305 22.16 <2e-16 ***
## Erfahrung 2.71668 0.12424 21.87 <2e-16 ***
## Training_Erfahrung -0.56502 0.02693 -20.98 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3314 on 246 degrees of freedom
## Multiple R-squared: 0.6688, Adjusted R-squared: 0.6648
## F-statistic: 165.6 on 3 and 246 DF, p-value: < 2.2e-16Typischerweise werden die Ergebnisse von Interaktionsanalysen in Zweifach-Interaktions-Plots vereinfacht dargestellt und kontrastieren dann die (geschätzen) Werte der abhängigen Variablen an den Rändern der Werte der interagierenden Variablen.
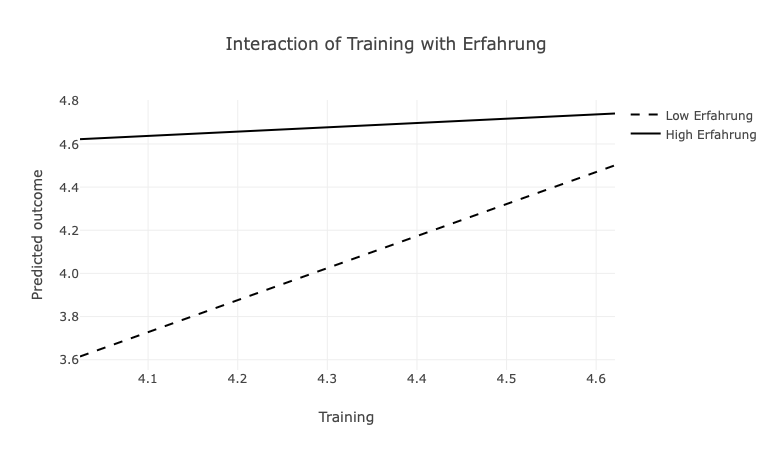Die Interaktionsabbildung weist einen positiven Beitrag von Trainings auf die Kompetenzen auf. Der Anstieg der Geraden ist jedoch steiler, wenn geringe Erfahrungen vorlagen (gestrichelte Linie). D.h. der Effekt von Trainings auf die Kompetenzen ist stärker, wenn die Erfahrungen der Mitarbeiter gering waren. Für diejenigen Mitarbeiter, die bereits Erfahrungen hatten, zeigt das Modell auch dann hohe Kompetenzen auf, wenn sie weniger Trainings durchgeführt haben (durchgezogene Linie). Die Abbildung zeigt insofern auf, dass die Kompetenzen der Mitarbeiter mit fehlenden Erfahrungen durch Trainings gefördert werden können.
Um den eigentlichen Effekt von Trainings auf die Kompetenz aufzuzeigen, wird die folgende Abbildung notwendig. Hier wird aufgezeigt, welchen Beitrag Trainings auf die Kompetenzen haben, wenn die Erfahrungen gering (links) oder hoch (rechts) ausgeprägt sind.
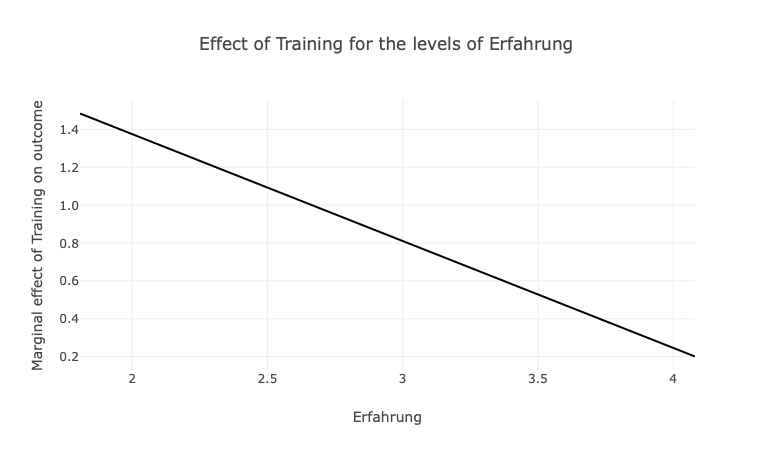
Hier wird aufgezeigt, dass Trainings die Kompentenzen vor allem dann fördern, wenn geringe Erfahrung vorliegen. Wenn viele Erfahrungen vorliegen, sinkt der Beitrag von Trainings deutlich.
Verschiedene Aspekte sprechen dafür, dass die Werte der interagierenden Variablen vor der Bildung des Produktterms standardisiert oder zumindest zentriert werden (Dawson, 2014). Besondere Beachtung sollte auf hohe Korrelationen zwischen der interagierenden Variablen gerichtet werden. Bei Korrelationen zwischen 0.3 und 0.5 wird von Dawson (2014) die zusätzliche Einbeziehung quadratischer Terme empfohlen, bei Korrelationen >0.5 sollten sie nicht unberücksichtigt bleiben (Dawson, 2014).
Die Bildung quadratischer Terme (nichtlineare Terme) erfolgt durch quadrieren der Werte einer Variablen. In Erweiterung zu diesem Vorgehen können auch Mehrfachinteraktionen (z. B. Interaktionen zwischen drei Variablen) operationalisiert werden (Dawson & Richter, 2006).
5.9.3 Interaktion
Es gibt zahlreiche Fälle, in denen die zwei unabhängige Variablen entweder durch
- eine gemeinsame Ursache,
- eine gemeinsame Wirkung oder
- eine gemeinsame Konsequenz
miteinander verbunden sind.
Auch wenn diese Variablen (tatsächlich oder nur scheinbar) voneinander unabhängig sind, können sie also in ihrer Wirkung voneinander abhängig sein, was meint, dass sich diese Variablen in ihrem Einfluss auf die abhängige Variable gegenseitig verstärken oder abschwächen. Insbesondere wenn nicht eindeutig zu klären ist, in welcher Richtung der Zusammenhang besteht oder gegenseitig gerichtete Beziehungen bestehen, wird dieses kontextuelle Zusammenwirken auf die abhängige Variable als Interaktion beschrieben.
Das folgende Beispiel geht von der Annahme aus, dass Entscheidungen in Organisationen grundsätzlich auf zwei Weisen getroffen werden können: in einem Top-Down- oder einem Bottom-Up-Prozess.
Beim Top-Down-Ansatz werden Entscheidungen von der höchsten Ebene der Hierarchie getroffen und nach unten weitergeleitet. Die Führungskräfte und das Top-Management legen Zielsetzungen und Strategien fest, die dann von den unteren Ebenen implementiert werden.
Im Gegensatz dazu werden beim Bottom-Up-Ansatz Entscheidungen von den Mitarbeitern oder den unteren Hierarchieebenen initiiert und nach oben kommuniziert, wo sie dann weiterentwickelt und formalisiert werden.
Beide Ansätze haben ihre Vor- und Nachteile und eignen sich je nach Kontext, Unternehmenskultur und der spezifischen Situation unterschiedlich gut. Es wird hier angenommen, dass kein hybride Ansatz der Entscheidungsbildung verfolgt wird, d.h. ein Prozess überwiegt, entweder Top-Down oder Bottom-Up. Der negative Zusammenhang zwischen beiden Ansätzen resultiert in der Tatsache, dass bei überwiegen des einen Ansatzes, der Erfolg des jeweils anderen Ansatzes reduziert wird.
##
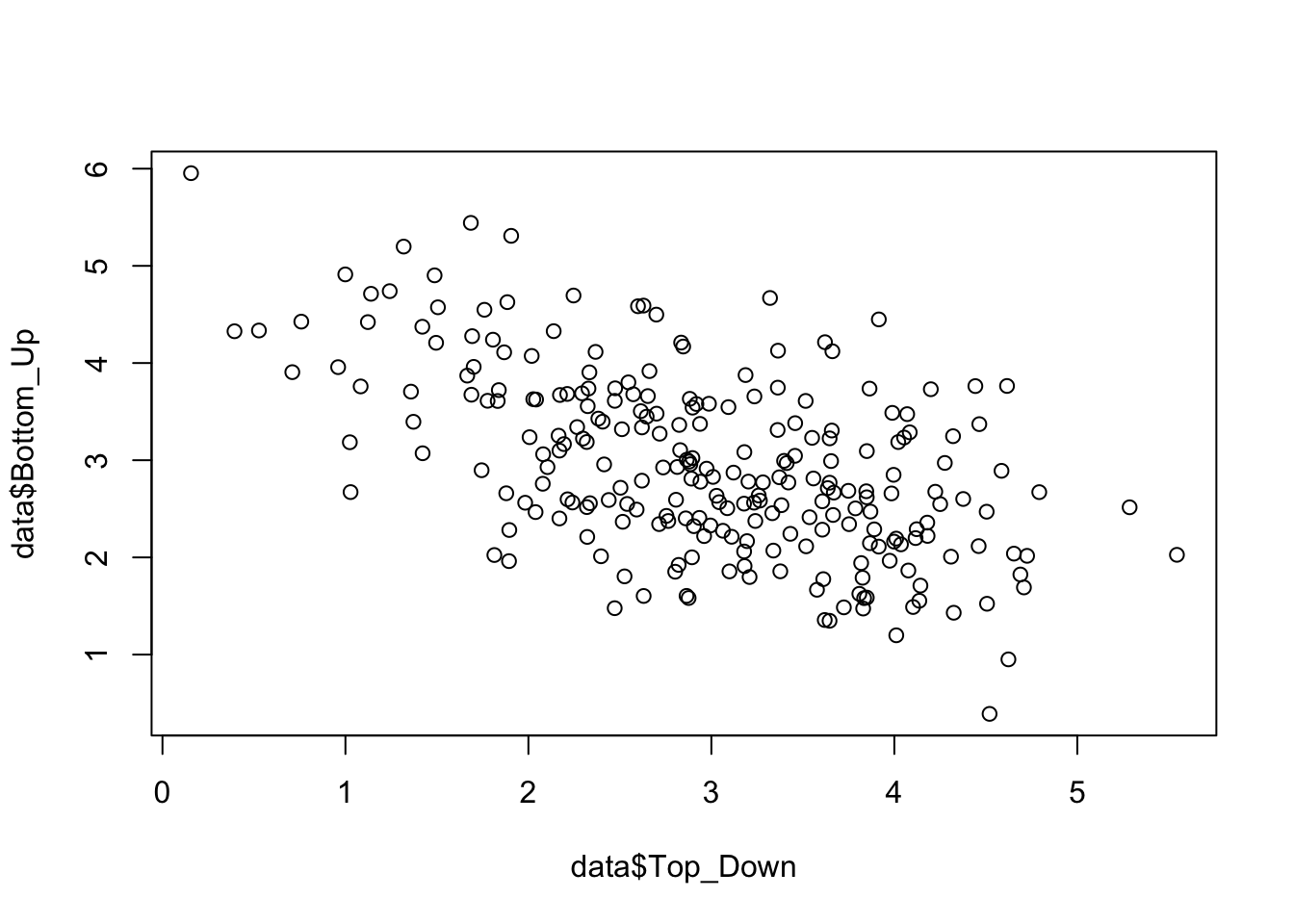
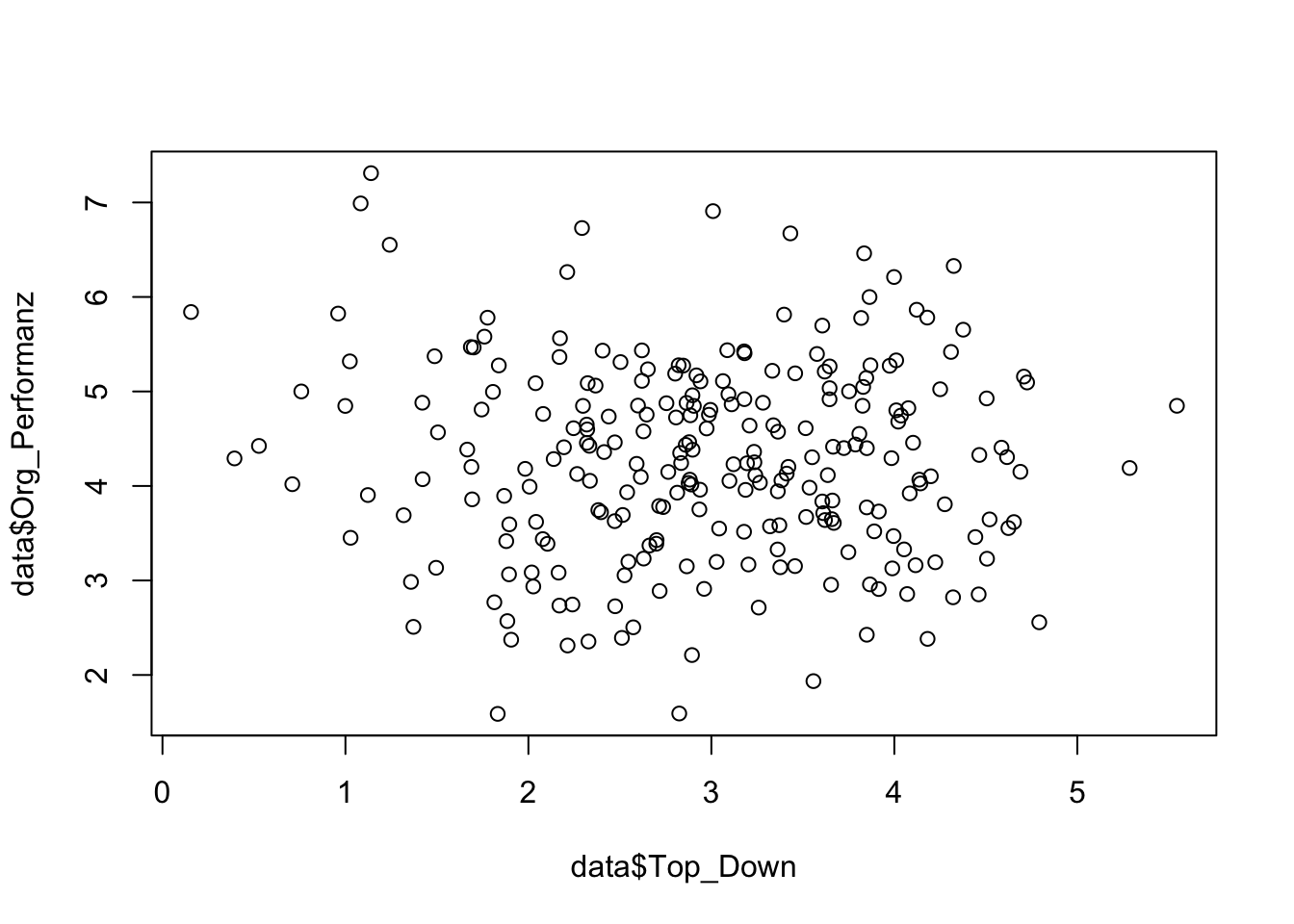
## Call:
## lm(formula = data$Org_Performanz ~ data$Top_Down + data$Bottom_Up)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.73428 -0.68948 -0.00561 0.69260 2.94989
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.35017 0.43844 9.922 <2e-16 ***
## data$Top_Down -0.03657 0.08030 -0.455 0.649
## data$Bottom_Up 0.01095 0.08527 0.128 0.898
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.032 on 247 degrees of freedom
## Multiple R-squared: 0.001704, Adjusted R-squared: -0.00638
## F-statistic: 0.2107 on 2 and 247 DF, p-value: 0.8101data$TD_BU = data$Top_Down * data$Bottom_Up
summary (lm(data$Org_Performanz~data$Top_Down + data$Bottom_Up + data$TD_BU))##
## Call:
## lm(formula = data$Org_Performanz ~ data$Top_Down + data$Bottom_Up +
## data$TD_BU)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.71461 -0.65420 0.00355 0.67340 2.73792
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.35056 0.72422 3.246 0.001335 **
## data$Top_Down 0.63294 0.21054 3.006 0.002918 **
## data$Bottom_Up 0.60823 0.19320 3.148 0.001846 **
## data$TD_BU -0.21209 0.06187 -3.428 0.000713 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.01 on 246 degrees of freedom
## Multiple R-squared: 0.04721, Adjusted R-squared: 0.0356
## F-statistic: 4.063 on 3 and 246 DF, p-value: 0.007655Bezüglich der organisationalen Leistung, weist der signifikante Koeffizienten des Produktterms auf eine Interaktion von Top-Down und Buttom-Up hin. Die folgende Abbildung zeigt auf, wie der positive Effekt des Top-Down-Ansatzes auf die organisationale Leistung von \(\beta_{low BU}=0.2\) (bei geringem Bottom-Up) auf \(\beta_{high BU}= -0.2\) (bei hohem Bottom-Up) sinkt. Der Bottom-Up-Prozess moderiert demnach den Einfluss des Top-Down-Ansatzes auf die organisationale Leistung negativ.
Die zweite Abbildung zeigt auf, wie der positive Effekt des Bottom-Up-Ansatzes auf die organisationale Leistung von \(\beta_{low TD}=0.2\) (bei geringem Top-Down) auf \(\beta_{high TD}= -0.2\) (bei hohem Top-Down) sinkt. Der Top-Down-Ansatzes moderiert also gleichermaßen den Einfluss des Bottom-Up-Prozess auf die organisationale Leistung negativ.
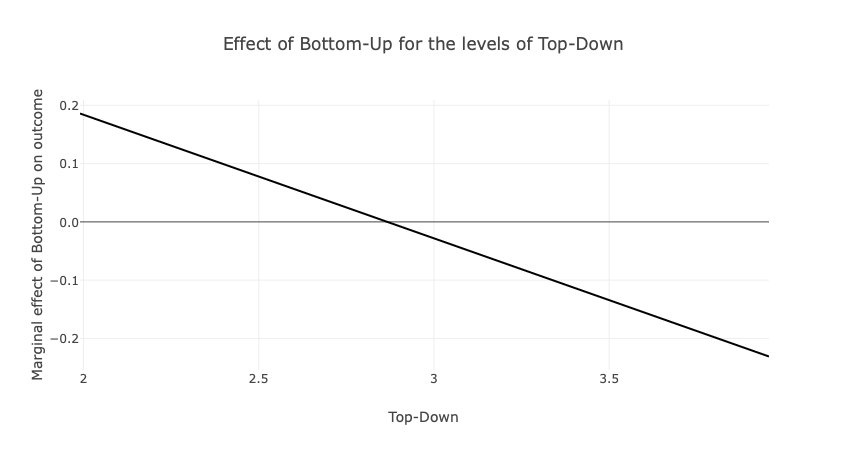
Für beide Ansätze gilt also, dass sie nur dann einen klaren Vorteil für die organisationale Leistung aufweisen, wenn der jeweils andere Ansatz nicht vorliegt. Die Interaktion zeigt sich in diesem Fall als Kreuz der beiden Regressionsgeraden.
