Kapitel 6 Aussagen & Logik
In der deduktiven Logik sind Aussagen Sätze oder Ausdrücke, die einen eindeutigen Wahrheitswert haben, also entweder wahr oder falsch sind, und die Grundlage für logische Schlussfolgerungen und Beweise bilden. Aussagen werden in den Sprach- und Kognitionswissenschaften als Propositionen bezeichnet und bilden die kleinstmöglichen Wissenseinheiten ab, die entweder wahr oder falsch sein können (Westermann, 2000, S. 69).
6.1 Elementaraussagen
Verknüpfen wir zwei elementare Aussagen (Propositionen) \(X\) und \(Z\) in logischer Weise, lassen sich anhand von Schlussregeln, die in der deduktiven Logik gelten, “Folgerungen mit Gewissheit aus den Prämissen ableiten” (Anderson, 1996, S. 304).
Die Propositionen \(X\) und \(Z\) bilden dann eine zusammengesetzte Aussage in Form einer Behauptung und können wahr sein oder falsch.
Weisen zwei Propositionen immer denselben Wahrheitswert auf, werden sie als äquivalent, d.h. symmetrisch bezeichnet. Schließt hingegen der Wahrheitswert einer Bedingung die Falschheit der anderen Bedingung ein, wird dies als kontravalent (asymmetrisch) bezeichnet. Darüber hinaus kann die Aussage der zwei Propositionen auch auf zwei weitere Implikationen verweisen: Suffizienz oder Notwendigkeit. Die folgende Tabelle zeigt die Wahrheitswerte der ursprünglichen Aussagen mit den Wahrheitswerten der verknüpften Aussagen.
\[ \begin{array}{|c|c|c|c|c|c|} \hline X & Z & Äquivalenz & Kontravalenz & Suffizienz & Notwendigkeit \\ \hline \text{wahr} & \text{wahr} & \text{wahr} & \text{falsch} & \text{wahr} & \text{wahr} \\ \text{wahr} & \text{falsch} & \text{falsch} & \text{wahr} & \text{falsch} & \text{wahr} \\ \text{falsch} & \text{wahr} & \text{falsch} & \text{wahr} & \text{wahr} & \text{falsch} \\ \text{falsch} & \text{falsch} & \text{wahr} & \text{falsch} & \text{wahr} & \text{wahr} \\ \hline \end{array} \]
6.1.1 Äquivalenz
Äquivalenz von X und Z bezieht sich also auf den Fall, dass X und Z immer den gleichen Wahrheitswert aufweisen. Entweder sind beide falsch (0) oder beide sind wahr (1).
\[\begin{bmatrix} x & z \\ 0 & 0 \\ 1 & 1 \\ \end{bmatrix}\]
Formal wird dies dargestellt durch: \[X \leftrightarrow Z\]
Werden “gemeinsame” Wirkungen dargestellt, lässt elementare Äquivalenz zwei Formen zu, die im folgenden Abschnitt beschrieben werden: 1) komplementäre Wirkung und 2) exklusive Wirkung.
Eine Substitution oder eine Negation zweier Bedingungen hinsichtlich eines Ergebnisses kann bei elementarer Äquivalenz empirisch nicht vorliegen, weil die eine Bedingung die andere nicht ersetzen kann (Substitution), wenn beide Bedingungen äquivalent (symmetrisch) vorhanden oder nicht vorhanden sind. In der Logik ist dies jedoch anders vorgesehen.
Nehmen wir an, dass Ergebnis \(Y\) hängt von \(X\) und \(P\) , einer weiteren Aussage, ab: \[ Y = X \wedge P\]
Weil \(X\) äquivalent zu \(Z\) ist \(X \leftrightarrow Z\), kann \(X\) in \(Y\) sicher duch \(Z\) ersetzt werden, ohne den Wahrheitswert von \(Y\) zu verändern. Die abgeleitete Formel wäre dann:
\[ Y' = Z \wedge P\]
Die Substitution aufgrund der Äquivalenz ist dann gültig, weil die Äquivalenzrelation eine beidseitige Implikation ist, was bedeutet, das \(X\) und \(Z\) hinreichend und notwendig füreinander sind und jede Wahrheit, die aus \(Y\) abgeleitet wirdm wenn \(X\) durch \(Z\) ersetzt wird, immer noch gültig ist und umgekehrt.
Die Äquivalenz der Bedingungen X und Z bedeutet, dass Bedingung X und Bedingung Z gleichwertig und daher austauschbar sind.
Da die Bedingung X notwendig für Y ist und Bedingung Z die Bedingung X ersetzen kann (aufgrund ihrer Äquivalenz), ist es zutreffend, dass auch Bedingung Z verwendet werden kann, um Y zu erreichen oder zu ermöglichen.
6.1.2 Kontravalenz
Kontravalenz bildet das Gegenstück zur Symmetrie und elementare Aussagen beziehen sich auf die Ungleichwertigkeit von grundlegenden Aussagen oder Bedingungen. Zwei Bedingungen mit dem entgegengesetzten Wahrheitswert sind demnach kontravalent, d.h. asymmetrisch.
\[\begin{bmatrix} x & z \\ 0 & 1 \\ 1 & 0 \\ \end{bmatrix}\]
Formal wird dies ausgedrückt durch: \[X \oplus Z \]
6.1.3 Suffizienz
Eine Aussage bzw. ein Ereignis \(X\) ist eine hinreichende Bedingung (sufficent condition) für eine Aussage \(Z\), wenn das Zutreffen von \(X\) ausreicht, um das Zutreffen von \(Z\) zu garantieren. Das heißt, wenn \(X\) wahr ist, dann muss auch \(Z\) wahr sein.
Formal ausgedrückt:
\[X \to Z\]
Der Pfeil als Symbol der Implikation von X nach Z wird sprachlich als \(X\) impliziert \(Z\), \(X\) ist hinreichend (suffizient) für \(Z\) oder ‘wenn X, dann Z’ gebraucht.
Nach Dul (https://bookdown.org/ncabook/advanced_nca2/glossary.html#glossary) ist die hinreichende Bedingung definiert als:
“A cause that always results in an outcome”. Logisch formuliert als \([(A \to B) \wedge A] \to B\) was den modus ponens aufzeigt, aber weil \(A \to B\) äquivalent ist zu \((\neg A) \lor B\) kann sich das Ergebnis (outcome) auch ohne die Bedingung manifestieren.
Durch die Wahrheitstafel ist diese Implikation so definiert, dass die Aussage \(X \to Z\) nur unter einer Bedingung falsch ist: Wenn X wahr und wenn Z falsch ist oder wie es Westermann (2000, S. 73) formuliert: „Aus Wahrem kann nicht Falsches folgen“.
Nehmen wir die beiden Aussagen X: “Google diskriminiert Frauen” und Z: “Google bezahlt Frauen ein geringeres Gehalt”, dann ist die Aussage \(X \to Z\) (Wenn Google Frauen diskriminiert, dann bezahlt Google Frauen ein geringeres Gehalt) definitionsgemäß nur dann falsch, falls Google Frauen diskriminiert, ihnen aber kein geringeres Gehalt zahlt.
Das Alltagsverständnis von Wenn-Dann-Aussage entspricht dabei nicht unbedingt der solcher Logik:
Die Aussage “Wenn Google Frauen diskriminiert, dann bezahlt Google Frauen ein geringeres Gehalt” ist nämlich auch für den Fall wahr, in dem “Google diskriminiert Frauen” nicht zutrifft (also falsch ist) und Frauen ein geringeres Gehalt gezahlt wird” (!).
Aus der Definition der Wahrheitstabelle kann also entnommen werden, dass eine Bedingung X hinreichend (sufficiency) für ein Ergebnis Z ist,
- wenn die Bedingung (X) und das Ergebnis (Z) zutreffen (Zeile 1),
- wenn weder Bedingung (X) noch Ergebnis (Z) zutreffen (Zeile 4) oder
- das Ergebnis (Z) ohne die Bedingung (X) auftritt (Zeile 3).
Selbst die “Aussage ‘Wenn 2 mal 2 gleich 5 ist, dann liegt Berlin an der Elbe’ ist aussagenlogisch sinnvoll, und sie ist, da Prämisse und Konklusion falsch sind, sogar wahr” (Westermann, 2000, S. 74).
Gelegentlich gibt die charakteristische Darstellung im Streudiagramm Hinweise auf einen Zusammenhang in Form einer hinreichenden Bedingung.
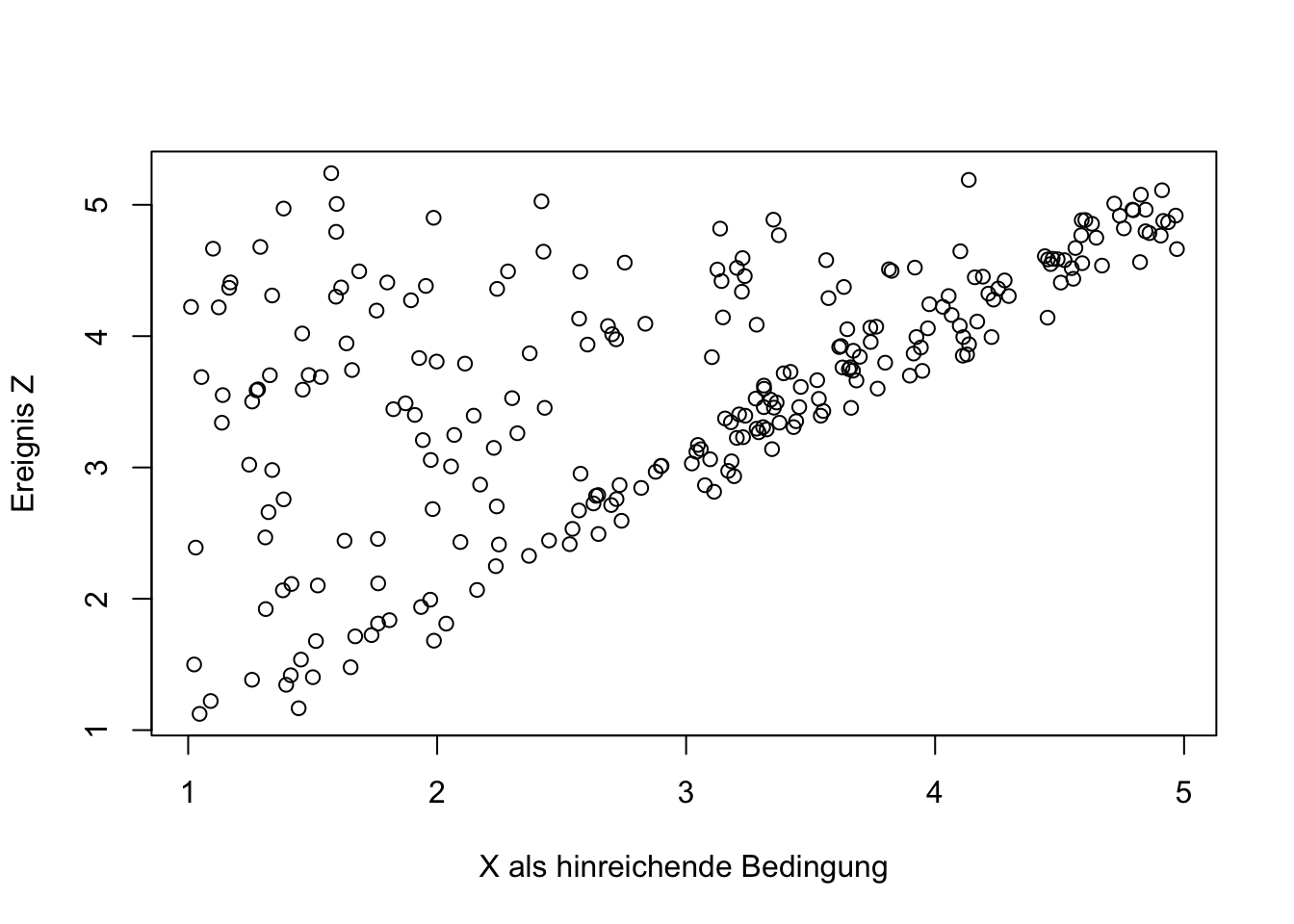
Der Ausdruck “hinreichend” (sufficiency) bezeichnet also die Situation, die Dul (2016, p.18) mit der Aussage beschreibt:“If success is present in cases without the condition, X is not necessary for Y. (Dul 2016, p.18)
6.1.4 Notwendigkeit
“Gilt die Aussage \(A \to B\), bezeichnet man \(A\) als hinreichende Bedingung für \(B\) und [umgekehrt gilt auch] \(B\) als notwendige Bedingung für \(A\)” (Westermann, 2000, S. 74).
Ein Ereignis \(X\) ist eine notwendige Bedingung (“necessary condition”) für ein Ergebnis \(Z\), wenn \(Z\) nie ohne \(X\) auftritt, oder wie es Dul (https://bookdown.org/ncabook/advanced_nca2/glossary.html#glossary) formuliert “A cause that must exist in order for the outcome to exist”.
\(X\) als notwendige Bedingung (necessary condition) für ein outcome \(Y\) wird formal geschrieben als \(X \leftarrow Y\). Die Definition in der Wahrheitstabelle zeigt drei Zeilen auf, in denen die Aussage, dass die Bedingung \(X\) für \(Z\) notwendig ist, wahr ist:
- wenn die Bedingung (X) und das Ergebnis (Z) zutreffen (Zeile 1),
- wenn weder Bedingung (X) noch Ergebnis (Z) zutreffen (Zeile 4) oder
- die Bedingung (X) ohne das Ergebnis (Z) zutrifft (Zeile 2).
Eine Bedingung \(X\) ist also nur dann keine notwendige Bedingung für \(Z\), wenn es Fälle gibt, in denen das Ergebnis \(Z\) eintritt ohne das die Bedingung \(X\) vorliegt.
Die Aussage, dass Bedingung X notwendig für Y ist, bedeutet, dass die Bedingung X eine Voraussetzung dafür ist, dass Y existiert, funktioniert oder erreicht wird.
Im Übrigen ist das Fehlen der Bedingung in Fällen ohne Ergebnis auch ein Indiz für die Suffizienz von Bedingung und Ergebnis. (Dul, 2016, S. 18) schreibt: “The absence of the outcome in cases without the condition is an indication of necessity of X and Y”.
Hinreichende und notwendige Aussagen beinhalten also beide das gemeinsame Eintreten von Bedingung und Ergebnis bzw. ihr gemeinsames Nicht-Eintreten In diesen beiden Zeilen der Wahrheitstafel sind Notwendigkeit und Suffizienz äquivalent.
Hinweise auf eine notwendige Bedingung bieten Streudiagramme, die den folgenden charakteristischen Verlauf aufzeigen.
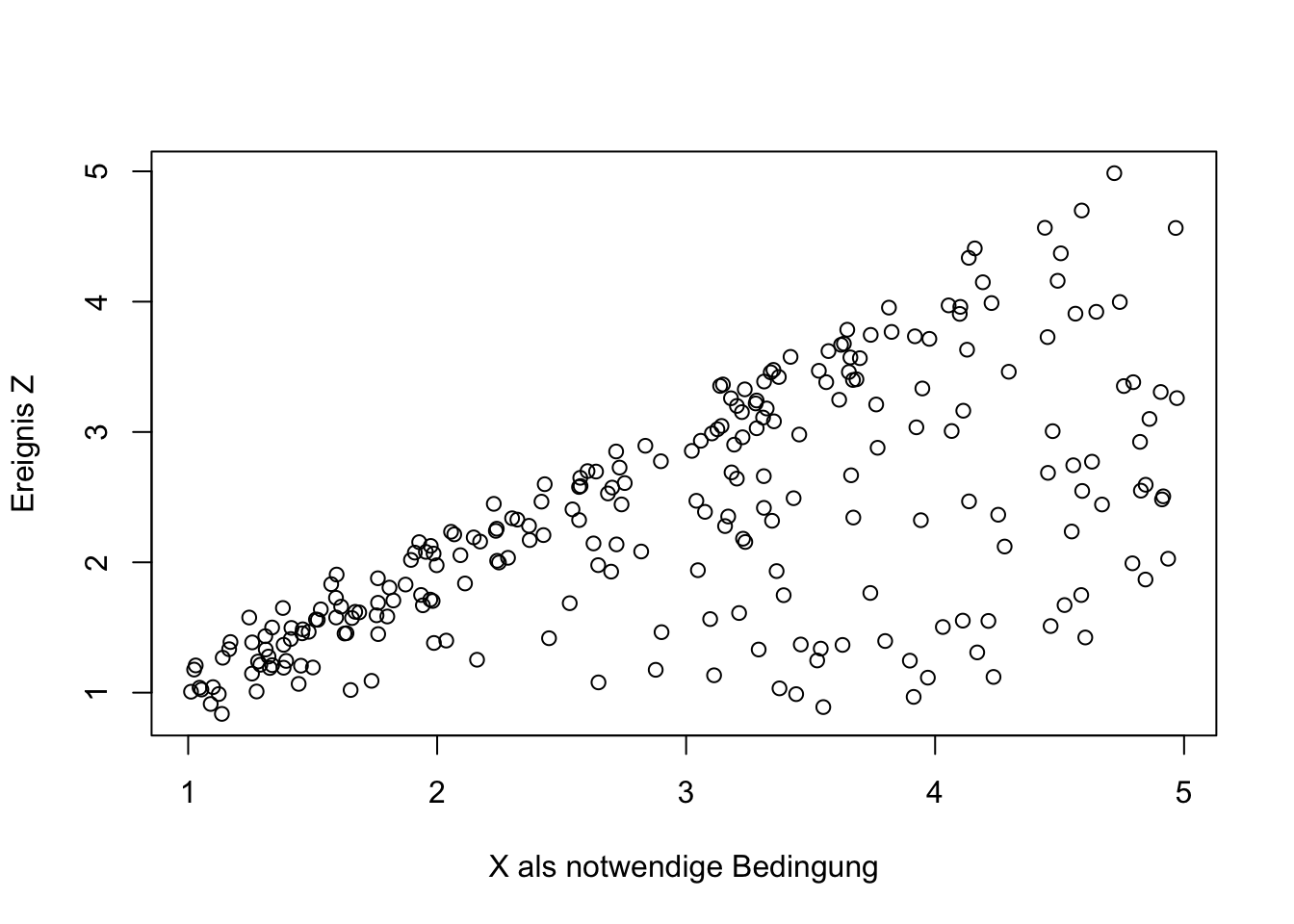
6.2 Interpretationen
Im Folgenden werden einige Begriffe, die häufig im Zusammenhang mit Interaktionen verwendet werden, in der Form definiert, wie sie logisch ableitbar sind, auch wenn sie umgangssprachlich häufig andere oder unspezifische Bedeutung annehmen.
Um diese Begriffe zu definieren werden logische Operatoren zur Verknüpfung der Prämissen verwendet. Diese Operatoren sind die Grundlage der Aussagenlogik und ermöglichen es, komplexe logische Strukturen aus einfacheren Aussagen zu bilden. Sie bestimmen dabei eindeutig, wie die einzelnen Aussagen (Bedingungen) kombiniert werden, um zu einer Schlussfolgerung (Begriff) zu gelangen.
6.2.1 Komplementarität (AND)
Komplementarität ist ein Konzept, dass auf die Wechselwirkung oder Ergänzung verschiedener Teile oder Aspekte eines Systems oder einer Struktur verweist, um ein Ganzes zu bilden oder um eine bestimmte Funktion zu erfüllen. So bildet z.B. die Nullhypothese das logische Komplement zur Alternativhypothese, die wir untersuchen (Westermann, 2000, S. 411).
Komplementarität bezeichnet logische Konjunktion (umgangssprachlich: “und”). Diese Verknüpfung ist wahr, wenn beide verbundenen Aussagen wahr sind.
In Matrix-Schreibweise formuliert:
\[\begin{pmatrix} x_1 & z_1 \\ x_2 & z_2 \\ x_3 & z_3 \\ x_4 & z_4 \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}= \begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\]
Ein Beispiel für solch eine Beziehung bietet das vereinfachte Wert-Erwartungs-Modell der Motivation. Der “Wert” bezieht sich dabei auf die subjektive Bedeutung oder Wichtigkeit einer bestimmten Handlung oder eines bestimmten Ziels für eine Person. Je höher der “Wert” ist, den eine Person einer Handlung oder einem Ziel beimisst, desto größer ist seine Motivation, dieses Ziel zu erreichen. Die “Erwartung” bezieht sich auf die Überzeugung einer Person, dass ihre Anstrengungen tatsächlich zur Erreichung des Ziels führen werden. Je höher die Erwartung einer Person ist, dass ihre Handlungen zu einem erfolgreichen Ergebnis führen, desto größer ist die Motivation, diese Handlungen auszuführen.
Das Modell drückt also aus, dass die Motivation einer Person als Produkt aus dem Wert des Ziels und der Erwartung resultiert, dass Anstrengungen zur Zielerreichung führen werden. Anders ausgedrückt, eine Person ist motiviert, wenn sie das Ziel als wichtig betrachtet und überzeugt ist, dass ihre Anstrengungen erfolgreich sein werden.
Werden “Wert” und “Erwartung” in einem multivariaten, additiven Regressionsmodell eingesetzt, zeigt das Ergebnis hohe positive und signifikante Koeffizienten für Wert und Erwartung auf.
##
## Call:
## lm(formula = Motivation ~ Wert + Erwartung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.90739 -0.35514 -0.00643 0.33838 1.07441
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.65350 0.10445 -15.83 <2e-16 ***
## Wert 0.56931 0.02385 23.87 <2e-16 ***
## Erwartung 0.58454 0.02350 24.88 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4276 on 247 degrees of freedom
## Multiple R-squared: 0.8245, Adjusted R-squared: 0.8231
## F-statistic: 580.3 on 2 and 247 DF, p-value: < 2.2e-16Obwohl “Wert” und “Erwartung” nicht korrelieren (siehe die folgende Abbildung), sind sie in Bezug auf die abhängige Variable Motivation verbunden. Gemäß der Ausdrucksweise von Pearl (2009a) sind diese Variablen sogenannte Collider”*. Sie sind im Modell über die Motivation miteinander verbunden und dies kann mit verzerrten Koeffizientenschätzungen einhergehen. Diese Verzerrung kann durch die Einbeziehung ihrer Interaktion als Produktterm \(Wert \cdot Erwartung\) in die Regressionsgleichung korrigiert werden.
##
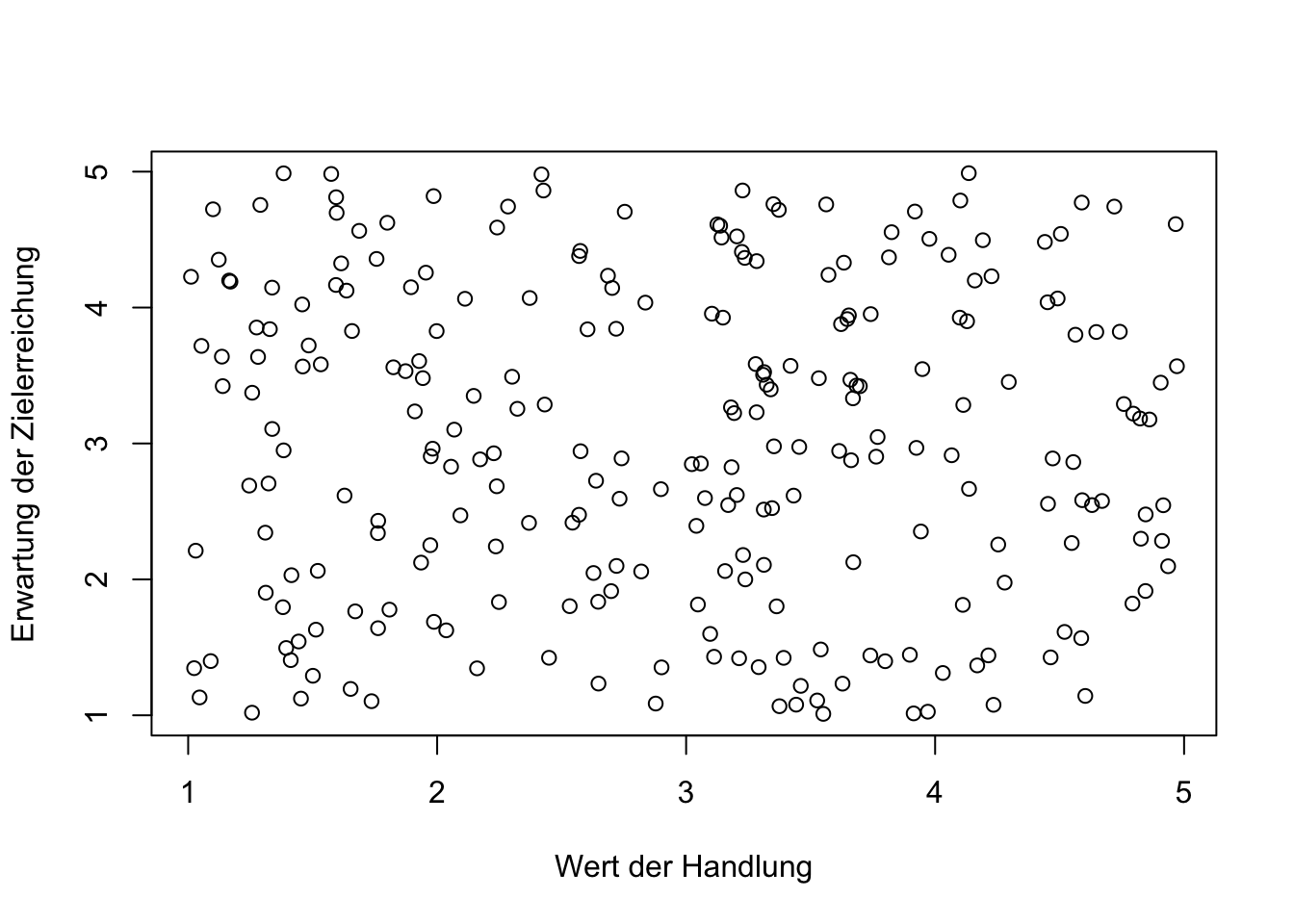
## Call:
## lm(formula = Motivation ~ Wert + Erwartung + Wert_Erwartung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.61172 -0.27876 -0.01755 0.29543 0.65543
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.089466 0.167437 0.534 0.594
## Wert -0.031422 0.053568 -0.587 0.558
## Erwartung 0.009944 0.051434 0.193 0.847
## Wert_Erwartung 0.198773 0.016574 11.993 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3404 on 246 degrees of freedom
## Multiple R-squared: 0.8893, Adjusted R-squared: 0.8879
## F-statistic: 658.5 on 3 and 246 DF, p-value: < 2.2e-16Das Ergebnis der Interaktionsanalyse zeigt einen signifikanten Koeffizienten für den Interaktionsterm auf. Aus der folgenden Abbildung geht hervor, dass “Wert” und “Erwartung” eine komplementäre Wirkung auf die Motivation aufweisen. Wenn nur eine der beiden Bedingungen hoch ausgeprägt ist, erreicht die Motivation lediglich moderate Beträge (\(\approx 1.5\)). Nur unter der Bedingung, das beide Aspekte (Erwartung und Wert) hoch ausgeprägt sind, resultiert Motivation mit einem Betrag in Höhe von \(\approx 3.5\).
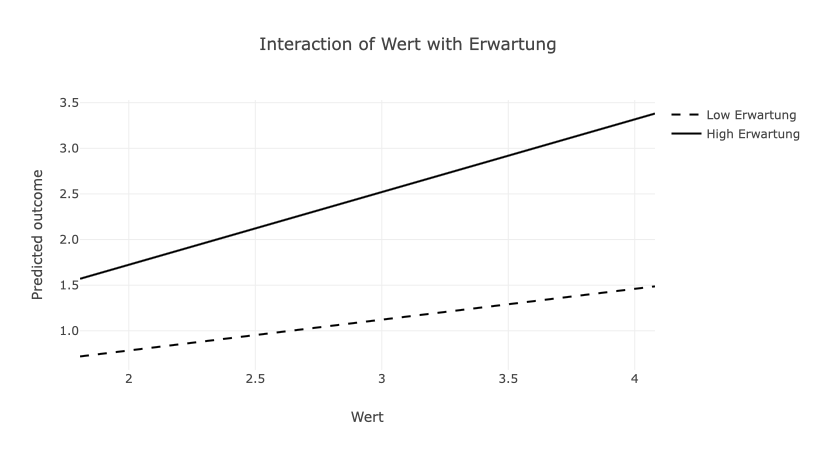
Die geschätzten Koeffizienten von Wert beschreiben nun den Beitrag von Wert zu Motivation, bei eineR durchschnittlichen Ausprägung von Erwartung. Umgekehrt zeigt der geschätzte Koeffizient von Erwartung nun den Beitrag, den Erwartung zu Motivation aufweist, wenn der Wert eine durchschnittliche Ausprägung aufweist. Die Einbeziehung des Produktterms führt in diesem Regressionsmodell zu einer höheren internen Validität, indem sie die ceteris-paribus-Bedingung aufzeigt, also der Tatsache, dass unterschiedliche Konsequenzen (bzw. Ausprägungen einer abhängigen Variable) auf unterschiedliche Ursachen (Ausprägungen der unabhängigen Variable) zurückgeführt werden können.
Im Ergebnis wird deutlich, dass Motivation nur durch das Zusammentreffen von Wert und Erwartung erreicht wird. Bildungssprachlich und logisch korrekt liegt hier eine ausschießlich komplementäre Wirkung vor.
6.2.2 Exklusion (NAND)
Eine Exklusion beschreibt das Konzept, bei dem durch Wahrheit von X und Z auf Falschheit von Y hinweist. Ein Ergebnis wird demnach erreicht, wenn Bedingung X und Bedingung Z nicht zutreffen oder wenn nur eine der beiden Bedingungen zutrifft. Treffen beide Bedingungen zu, ist das Ergebnis falsch bzw. das Ergebnis wird nicht erreicht.
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \\ 1 \\ 0 \end{bmatrix}\]
Preisgestaltung und Wettbewerbsintensität sind zwei wesentliche Faktoren, die den Absatz eines Produktes oder einer Dienstleistung maßgeblich beeinflussen. Typischerweise führen niedrige Preise bei geringer Konkurrenz zu hohen Verkaufszahlen. In Marktsegmenten mit wenig Wettbewerb kann die Einzigartigkeit eines Produkts oder einer Dienstleistung (Alleinstellungsmerkmale) einen höheren Preis rechtfertigen, was oft ebenfalls einen hohen Absatz zur Folge hat. Wenn Unternehmen ihre Produkte oder Dienstleistungen in einem stark umkämpften Markt zu niedrigen Preisen anbieten (Preisführerschaft), kann dies auch zu hohen Verkaufszahlen führen. Treffen jedoch hohe Preise auf eine hohe Konkurrenz, ist in der Regel mit einem geringeren Absatz zu rechnen.
set.seed(1899)
n=250
Preis <- runif(n,1,5)
Wettbewerb <- runif(n,1,5)
Absatz = 5- (Preis * Wettbewerb)/5- runif(n,-0.6,0.6)
par(mfrow=c(1,2))
plot (Preis, Absatz, xlab="Preis", ylab= "Absatz")
plot (Wettbewerb, Absatz, xlab="Wettbewerb", ylab= "Absatz")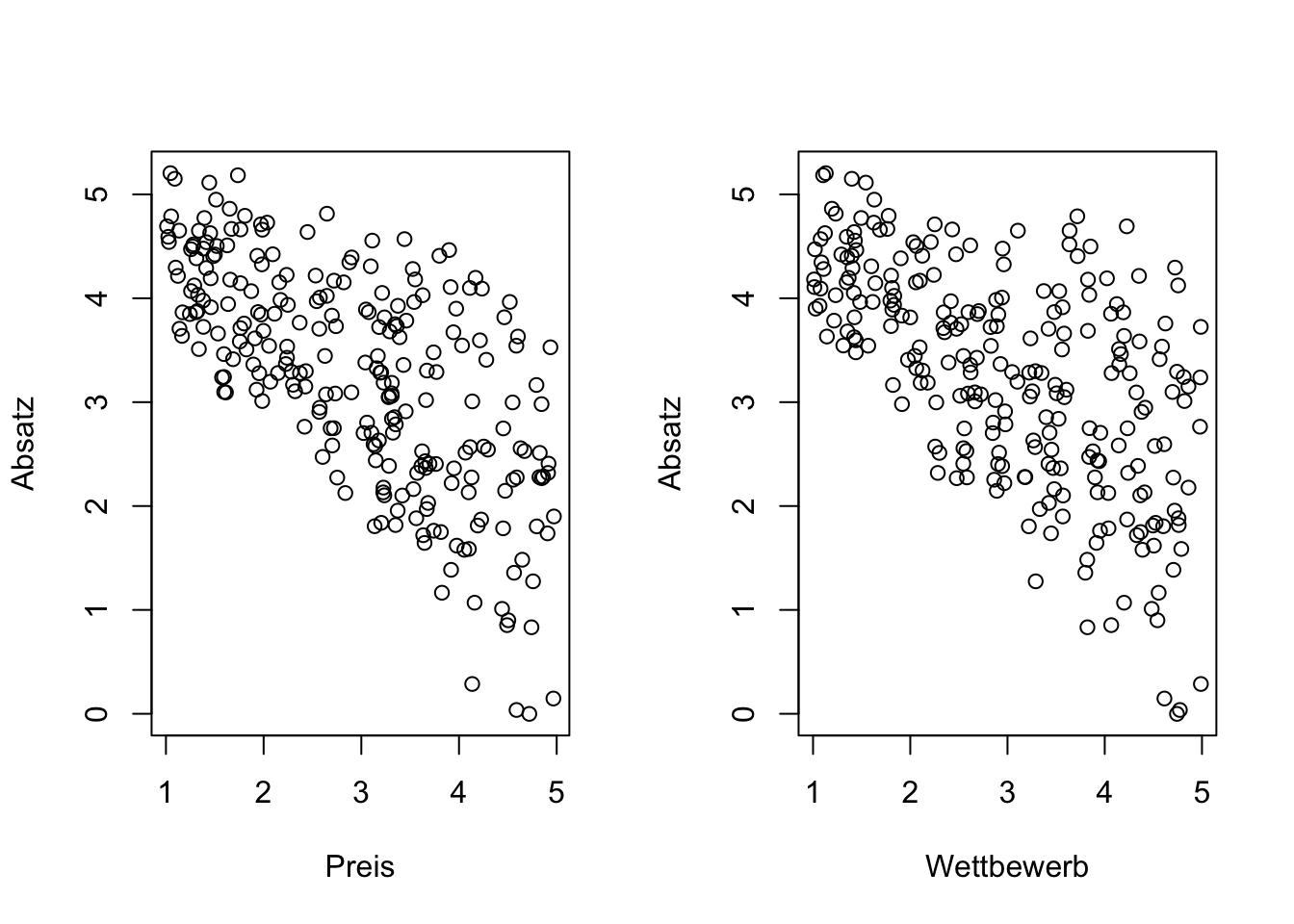
##
## Call:
## lm(formula = Absatz ~ Preis + Wettbewerb + Preis_Wettbewerb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.61172 -0.27876 -0.01755 0.29543 0.65543
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.089466 0.167437 30.396 <2e-16 ***
## Preis -0.031422 0.053568 -0.587 0.558
## Wettbewerb 0.009944 0.051434 0.193 0.847
## Preis_Wettbewerb -0.201227 0.016574 -12.141 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3404 on 246 degrees of freedom
## Multiple R-squared: 0.8981, Adjusted R-squared: 0.8969
## F-statistic: 722.7 on 3 and 246 DF, p-value: < 2.2e-16Die Koeffizienten von Preis und Wettbewerb sind nicht signifikant und der Produktterm ist signifikant negativ. Die Darstellung als Interaktionsplot zeigt auf, dass ein geringer Preis bei geringem Wettbewerb mit dem höchsten Absatz einhergeht. Ist der Wettbewerb stark ausgeprägt und liegt ein geringer Preis vor, ist ebenfalls ein hoher Absatz zu verzeichnen. Gleiches trifft zu, wenn geringer Wettbewerb mit hohem Preis einher geht. Lediglich bei hohem Wettbewerb und hohem Preis sind deutliche Einbußen im Absatz zu verzeichnen.
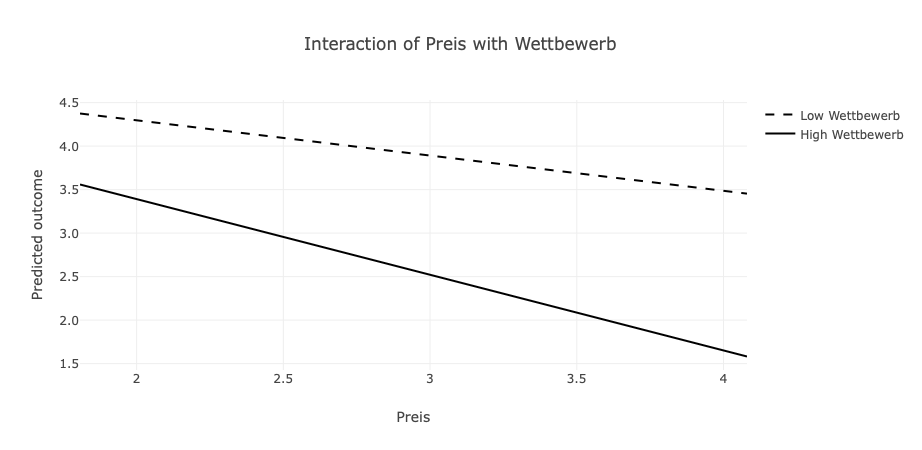
6.2.3 Substitution (OR)
Die Substitution ist ein grundlegendes Konzept, das beschreibt, dass etwas Bestimmtes durch etwas Anderes ersetzt werden kann.
Entgegen dem Alltagsverständniss ist die logische Operation X OR Z (X \(\lor\) Z) immer dann wahr, wenn mindestens einer der beiden Bedingungen wahr ist.
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \end{bmatrix}\]
Um Missverständlichkeiten zu vermeiden, sieht die Logik das “exklusive oder”: X xor Z (X\(\oplus\) Z) vor. Das “exklusive oder” ist nur wahr, wenn genau einer der Operanden wahr ist, nicht aber beide.
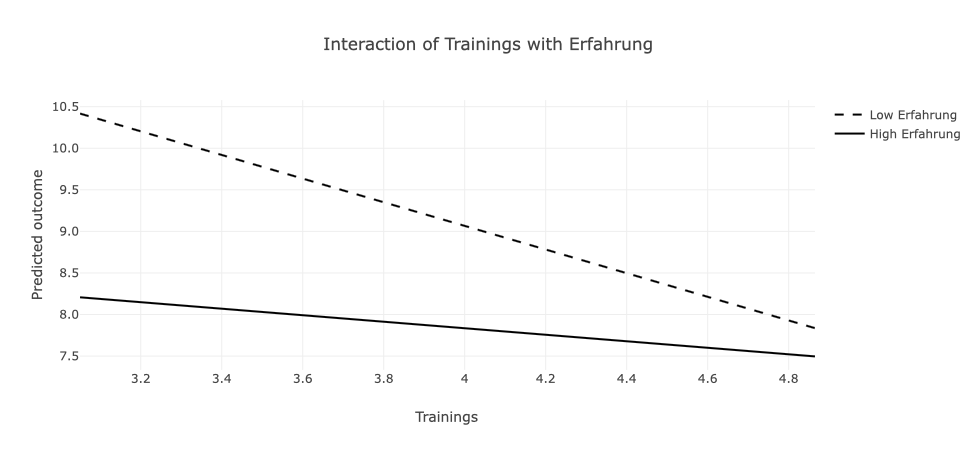
Im umgangssprachlichen Beschreiben von Zuständen oder Prozessen bezieht sich Substitution darauf, dass ein bestimmtes Ergebnis durch eine von zwei Bedingungen erreicht werden kann. Übertragen auf das Beispiel des Unternehmens, dass Erfahrung und Trainings der Mitarbeiter bzgl. der Kompetenz untersucht (Abschnitt: Additive Effekte), kann die Kompetenz demnach entweder aus Erfahrung oder aus Trainings resultieren. Mit anderen Worten, wenn keine Erfahrung vorhanden ist, müssen Trainings durchgeführt werden.
Formal ausgedrückt trifft das Ergeignis \(y\) zu, wenn entweder das Ereignis \(x\) zutrifft, das Ereignis \(z\) zutrifft oder beide Ereignisse (\(x\) & \(z\)) zutreffen. In Matrixschreibweise ergibt sich für den Fall, dass \(x\) und \(z\) austauschbar sind, um \(y\) zu erreichen (Substitute):
Training_Erfahrung = Training * Erfahrung
summary (lm (Kompetenz ~ Training + Erfahrung + Training_Erfahrung))##
## Call:
## lm(formula = Kompetenz ~ Training + Erfahrung + Training_Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.85963 -0.20336 0.03828 0.18249 0.81553
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.26598 0.52833 -13.75 <2e-16 ***
## Training 2.50499 0.11305 22.16 <2e-16 ***
## Erfahrung 2.71668 0.12424 21.87 <2e-16 ***
## Training_Erfahrung -0.56502 0.02693 -20.98 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3314 on 246 degrees of freedom
## Multiple R-squared: 0.6688, Adjusted R-squared: 0.6648
## F-statistic: 165.6 on 3 and 246 DF, p-value: < 2.2e-16Die Ergebnisse zeigen auf, dass der ein Mangel an Erfahung durch Trainings substituiert werden kann. Trainings fördern Kompetenz, Erfahrung fördert Kompetenz, der Interaktionsterm ist signifikant.
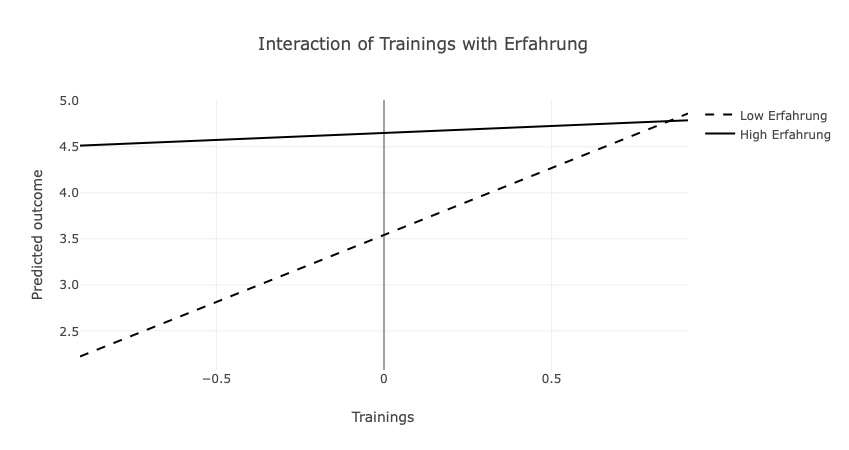
Wenn keine Erfahrung vorhanden ist, können Trainings den positiven Einfluss von Erfahrung auf die Kompetenz kompensieren.
6.2.4 Negation (NOR)
In ähnlicher Weise könnte untersucht werden, ob die Fehlerquote durch Trainings oder Erfahrung reduziert werden kann.
Diese Wirkungsform wird als Negation bezeichnet und beschreibt das grundlegende Konzept, dass ein Ergebnis (Fehler) durch die eine (Training) oder eine andere Bedingung (Erfahrung) verhindert werden kann. Wenn also keine Erfahrung vorhanden ist, kann ein Training das Auftreten von Fehlern verhindern.
Formal gesprochen trifft \(y\) zu, wenn weder \(x\) noch \(z\) zutrifft. In Matrixschreibweise ergibt sich für den Fall, dass \(x\) und \(z\) eine Negation für \(y\) darstellen:
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\]
#Training_Erfahrung = Training * Erfahrung
summary(lm(Fehler ~ Training + Erfahrung + Training_Erfahrung))##
## Call:
## lm(formula = Fehler ~ Training + Erfahrung + Training_Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.99087 -1.08516 0.07587 1.16585 2.96445
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 19.0685 2.3089 8.259 9.10e-15 ***
## Training -2.2525 0.4941 -4.559 8.10e-06 ***
## Erfahrung -2.3204 0.5429 -4.274 2.75e-05 ***
## Training_Erfahrung 0.4467 0.1177 3.795 0.000186 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.448 on 246 degrees of freedom
## Multiple R-squared: 0.09409, Adjusted R-squared: 0.08305
## F-statistic: 8.517 on 3 and 246 DF, p-value: 2.102e-05Dieses Regressionsmodell legt nahe, dass die Fehler dann auftreten, wenn weder Trainings noch Erfahrung vorliegen. Sowohl Training als auch Erfahrung können die Fehlerquote reduzieren und die geringste Fehlerquote liegt vor, wenn Erfahrung vorliegen und Trainings durchgeführt werden.
6.3 Merkmalsskalierung
In den Daten, die der folgenden Abbildungen zugrunde liegen, weisen für die Merkmale \(X\) und \(Z\) einen Wertebereich von 1 bis 5, einen Stichprobenmittelwert von \(\bar x= \bar z = 3.0\) und Standardabweichungen von \(SD_x=SD_z=1\) auf. Dies ist ähnlich der Datengrundlage, die aus Ratingskalen mit den Kategorien “trifft garnicht zu”, “trifft eher nicht zu”, “teils/ teils”, “trifft eher zu” und “trifft vollständig zu” resultieren.
Die Abbildungen zeigen die Plots jeweils für negative und positive Koeffizienten \(\beta_1\) und \(\beta_2\) bei einem positiven Koeffizienten (\(\beta_3=1.0\)) des Produkt-Terms.
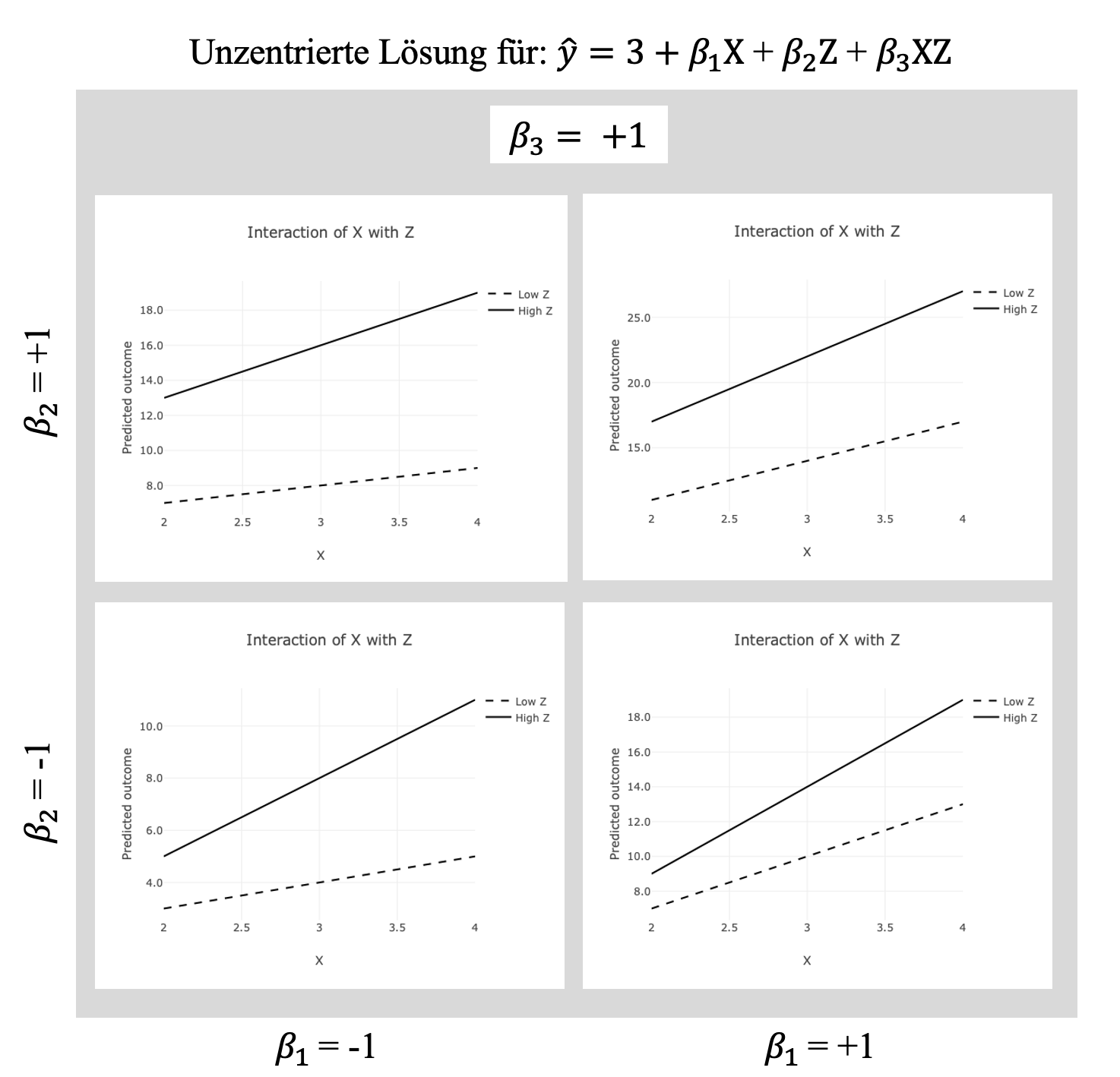
Auf der Abszisse ist für \(X\) der Bereich von \(\bar x - SD_x\) bis \(\bar x + SD_x\) dargestellt. Die Linien zeigen den (mittels Regressionsgleichung) geschätzten Betrag von \(\hat y\) für geringe (\(\bar z - SD_z\)) vs. hohe (\(\bar z + SD_z\)) Ausprägung von \(Z\). In der Abbildung mit der unzentrierten Lösung zeigen alle vier Plots ein ähnliches Bild auf. Bei einer geringen Ausprägung von Z (gestrichelte Linie) steigt die prognostizierte \(\hat Y\) mit steigendem \(X\).
Liegen für \(X\) und \(Z\) negative Koeffizienten (\(\beta_1 = \beta_2 = -1\)) vor (unten links in der Abbildung), ergibt sich aus der Schätzgleichung:
\[\hat y = \beta_0 + \beta_1 \cdot x + \beta_2 \cdot z + \beta_3 \cdot x \cdot z \] bei geringem \(x_{low} = 3 - 1 = 2\) und geringem \(z_{low} = 3 - 1 = 2\)
\[\hat y = 3 + (-1 \cdot 2) + (-1 \cdot 2) + (1 \cdot 2 \cdot 2) \]
\[ \hat y = 3 + (-2) + (-2) + (4) = 3 \]
ein prognostiziertes \(\hat y=3\). Wird für eines der Merkmale (\(X\) oder \(Z\)) ein hoher Betrag in die Schätzgleichung eingesetzt, steigt das prognostizierte Ergebnis auf einen Betrag von \(\hat y = 5\). Werden für \(X\) und \(Z\) hohe Beträge in der Schätzgleichung verwendet, ergibt sich \(\hat y = 11\).
Inhaltlich würde dies eine “AND”-Operation im Sinne einer komplementären Wirkung von \(X\) und \(Z\) auf \(Y\) nahelegen. Die gleiche Empfehlung resultiert aus der Abbildung für positive Koeffizienten \(\beta_1 = \beta_2 = +1\). Das geringste \(\hat y=11\) wird für die Kombination aus geringem \(X\) und geringem \(Z\) prognostiziert. Liegt für eines der Merkmale (\(X\) oder \(Z\)) ein hoher Betrag vor, ergibt sich \(\hat y = 17\). Das höchste \(\hat y = 27\) wird jedoch für die Situation prognostiziert, in welcher \(X\) und \(Z\) hohe Ausprägungen aufweisen.
Die Plots oben links und unten rechts zeigen die Verläufe für die Situation, in welcher einer der Koeffizienten \(\beta_1\) oder \(\beta_2\) einen negativen Betrag annimmt, während der andere sowie der Koeffizienten des Produktterms weiterhin positiv ausfallen.
In beiden Plots beträgt das \(\hat y = 7\), wenn \(X\) und \(Z\) gering ausgeprägt sind und in beiden Plots beträgt das \(\hat y = 19\) für den Fall, dass \(X\) und \(Z\) hoch ausgeprägt sind.
Sind die Merkmale \(X\) und \(Z\) nicht symmetrisch ausgeprägt, also wenn ein hoch ausgeprägtes Merkmal \(X\) mit einem gering ausgeprägten Merkmal \(Z\) einhergeht, zeichnet sich ein anderes Bild ab. Ein höheres \(\hat y = 13\) wird jeweils für dasjenige Merkmal erwartet, dass den positiven Koeffizienten \(\beta\) aufweist, während ein geringeres \(\hat y = 9\) für das Merkmal erwartet wird, welches den negativen Koeffizienten aufweist.
Als inhaltliche Interpretation würde hier dargestellt werden, dass der positive Zusammenhang zwischen dem Merkmal mit dem positiven Koeffizienten durch die Interaktion intensiviert wird.
Der positive Koeffizient eines Merkmals \(X\) (unten rechts) lässt ein geringes \(\hat y\) erwarten, falls \(X\) gering ausgeprägt ist. Bei einer hohen Ausprägung des Merkmals \(X\) wird ein höheres \(\hat y\) erwartet. Der Beitrag von \(X\) zu \(\hat y\) besteht dabei in zwei Termen der Gleichung mit jeweils positivem \(\beta\): \(\beta_1 \cdot x\) und \(\beta_3 \cdot x \cdot z\).
Betrachten wir im Folgenden eine zentrierte Lösung für den Fall einer symmetrischen Skala. Die Daten für \(X\) und \(Z\) unterscheiden sich lediglich darin, dass sie einen Wertebereich von -2 bis +2 aufweisen. Die resultierenden Mittelwerte sind für \(\overline x = \overline z = 0\) und die Standardabweichungen unetrscheiden sich nicht vom ersten Beispiel \(SD_x=SD_z=1\). Es zeigt sich ein ganz anderes Bild.
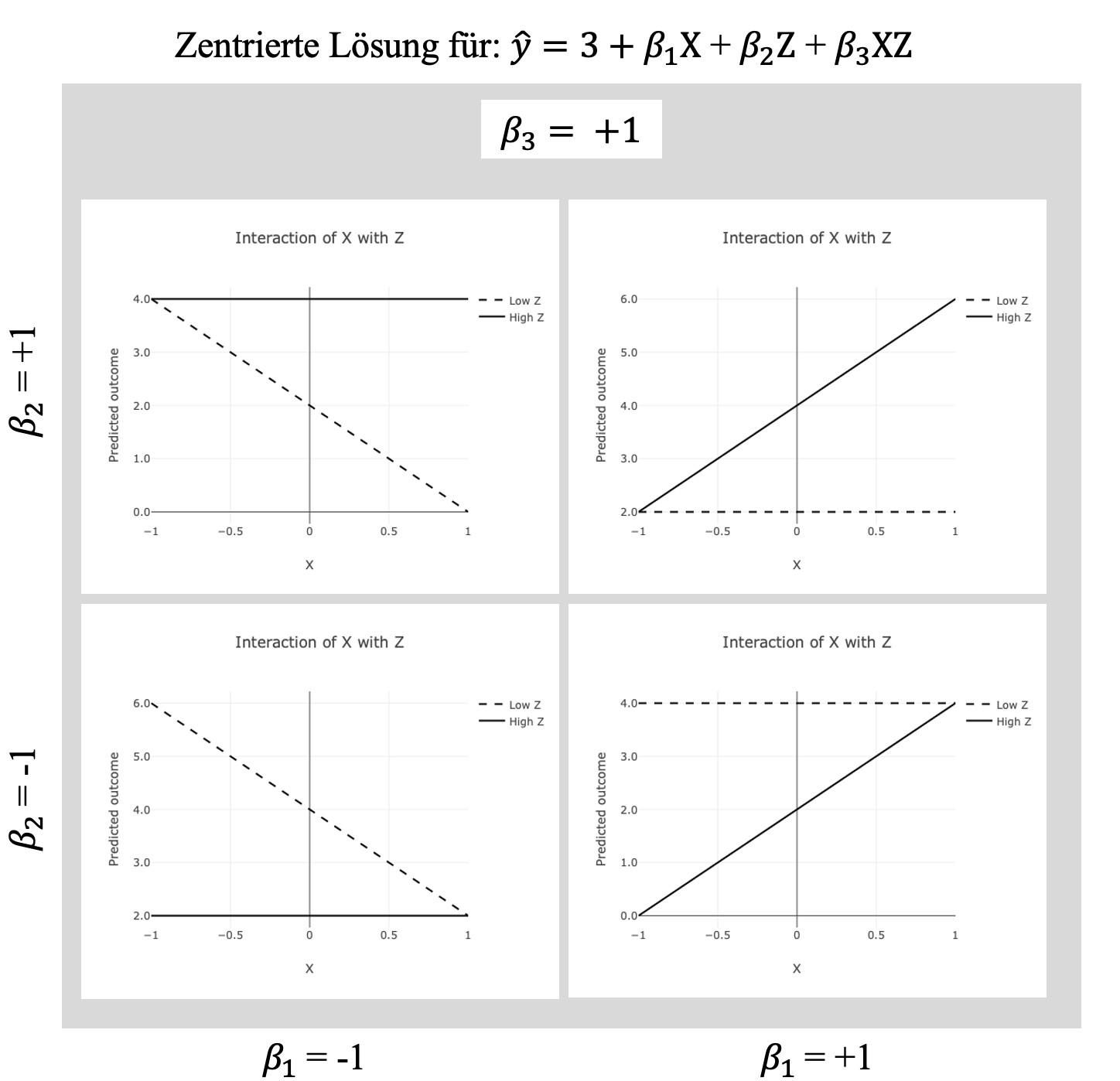
Oben rechts wird eine klare komplementäre Wirkung aufgezeigt. Nur wenn beide Merkmale hoch ausgeprägt sind, wird auch ein hohes \(\hat y\) erwartet.
Unten links wird eine klare Negation aufgezeigt. Nur wenn weder \(X\) noch \(Z\) hoch ausgeprägt sind, wird ein hohes \(\hat y\) erwartet.
Der Plot oben links zeigt die Situation auf, in der dass Ergebnis vorliegt wenn \(X\) gering ist, es sei denn, dass \(Z\) ebenfalls vorliegt. Das Ergebnis Y wird als materielle Implikation bezeichnet, wobei \(Z\) notwendig \(X\) ist, damit das Ergebnis wahr ist. Das Ergebnis kann also nur erreicht werden, wenn \(Z\) eine notwendige Bedingung für \(X\) ist. Anders formuliert, das Ergebnis ist nur dann wahr, wenn \(X\) niemals ohne \(Z\) auftritt.
Unten rechts liegt das Ergebnis vor, wenn \(Z\) gering ist, es sei denn, dass \(X\) vorliegt. Das Ergebnis Y wird auch hier als materielle Implikation bezeichnet, wobei in diesem Fall \(X\) eine notwendige Bedingung für \(Z\) ist, damit das Ergebnis wahr ist.
**Drei Fakten können aus dieser Ergebnissdarstellung abgeleitet werden:
- Erstens unterscheidet sich die inhaltliche Interpretation der Ergebnisse je nach eingesetzter Methode der Interaktionsbildung (unzentrierte Lösung vs. zentrierte Lösung),
- zweitens ist es nicht irrelevant, in welchem Wertebereich die Merkmale skaliert sind und
- drittens kann über die Hypothesen nicht allein anhand der Signifikanz oder der Richtung (positiv vs. negativ) der Koeffizienten entschieden werden.
Die Richtung und Ausprägung der Koeffizienten, sowie die damit verbundene Signifikanz, entscheiden lediglich darüber, wie die vom Regressionsmodell geschätzten Werte zu der höchsten Übereinstimmung mit den empirischen Daten gelangen. Um Hypothesen zu prüfen und inhaltliche Ableitungen zu tätigen, sind (über die Signifikanz des Produkt-Term-Koeffizienten hinaus) die geschätzten Werte für die entsprechenden Ausprägungen der unabhängigen Variablen zu bestimmen und auf signifikante Unterschiede zu prüfen.**
Diese Überlegungen beziehen sich auf unterschiedliche Wertebereiche von Daten, unabhängig davon, ob sie aufgrund der Skalierung oder ihrer Aufbereitung (z.B. Faktorwerte) einen negativen Wertebereich zulassen.
Insbesondere wenn die Daten unterschiedliche Wertebereiche einschließen, ist dies auch in der grafischen Darstellung zur inhaltlichen Interpretation zu berücksichtigen.
6.3.1 Zentrierung
Viele Quellen empfehlen eine Zentrierung der Variablen, bevor das Produkt der interagierenden Variablen gebildet wird (Dalal & Zickar, 2012; Dawson, 2014; Ludtke, 2008). Während dies in Strukturgleichungsmodellen (SEM) routinemäßig angenommen wird (Marsh, 2013, S. 376), kann dies in Regressionsmodellen erreicht werden, indem die Differenz des Stichproben-Mittelwertes von den einzelnen Wert gebildet oder eine z-Standardisierung durchgeführt wird.
Einige Autoren empfehlen die Zentrierung, um die Interpretation in der Darstellung zu erleichtern (Dawson, 2014) oder diskutieren Zentrierung im Kontext von Kollinearität (Dalal & Zickar, 2012). Entgegen der Aussage, dass Zentrierung keinen Unterschied im Nachweis von Moderationseffekten macht, (z.B. “In the vast majority of cases, this makes no difference to the detection of moderator effects; however, each method confers certain advantages in the interpretation of results.” (Dawson, 2014, S. 2), hat eine Zentrierung inhaltliche Konsequenzen für die Interpretation.
Wenn zwei unzentrierte Variablen geringe Werte aufweisen, ist ihr Produkt immer kleiner, als wenn beide Variablen hohe Werte aufweisen.
Durch jede Form von Zentrierung zweier Variablen ergibt das Produkt dieser Variablen auch dann einen positiven Wert, wenn beide interagierende Variablen geringe Werte (< 0) aufweisen.
Übertragen auf das Beispiel der Motivation wird die paradoxe Aussage verdeutlicht. Entsprechend des Wertebereiches wäre bei zentrierten Werten eine hohe Motivation für den Fall zu erwarten, in dem Wert und Erwartung beide hoch ausgeprägt sind, aber auch für den Fall, dass das Ziel einen geringen Wert hat und die Erwartung gering ist, dieses Ziel zu erreichen.
In der Matrixschreibweise trifft das Ergebnis y=1 also nicht nur dann zu, wenn x=1 und z=1 zutreffen (Komplementär), sondern auch wenn x=-1 und z=-1. Diese Situation wird bildungssprachlich und logisch korrekt als symmetrisch, äquivalent oder als ausgerichtet (aligned) bezeichnet.
\[\begin{pmatrix} x_1 & z_1 \\ x_2 & z_2 \\ x_3 & z_3 \\ x_4 & z_4 \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix}=\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix}\]
Wert_mz <- Wert - mean(Wert)
Erwartung_mz <- Erwartung - mean(Erwartung)
Wert_Erwartung_mz =Wert_mz * Erwartung_mz
summary(lm(Motivation ~ Wert_mz + Erwartung_mz + Wert_Erwartung_mz))##
## Call:
## lm(formula = Motivation ~ Wert_mz + Erwartung_mz + Wert_Erwartung_mz)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.61172 -0.27876 -0.01755 0.29543 0.65543
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.78928 0.02153 83.09 <2e-16 ***
## Wert_mz 0.56728 0.01898 29.88 <2e-16 ***
## Erwartung_mz 0.59506 0.01872 31.78 <2e-16 ***
## Wert_Erwartung_mz 0.19877 0.01657 11.99 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3404 on 246 degrees of freedom
## Multiple R-squared: 0.8893, Adjusted R-squared: 0.8879
## F-statistic: 658.5 on 3 and 246 DF, p-value: < 2.2e-16Tatsächlich weist die Regression mit mittelwertzentriertem Produkt-Term statistische Signifikanz für alle Koeffizienten auf, obwohl bekannt ist, dass nur das Produkt (Wert x Erwartung) in den Daten determiniert ist.
Modellvergleich
Wird das additive Modell (ohne Produkt-Term) und das non-additive Modell in der unzentrierten Lösung (siehe Kapitel Interpretationen - Komplementarität) sowie das Modell mit zentrierter Lösung verglichen, werden je nach eingesetzter Methode unterschiedliche Ergebnisse aufgezeigt.
Im ersten Modell wurden Wert und Erwartung als additive Terme in der Regressionsgleichung eingefügt. Die Koeffizienten für Wert und Erwartung sind hoch signifikant (p<0.001) und die Varianzaufklärung des Modells beträgt \(R^2=0.82\).
In das zweite Modell wurde der Produktterm der unzentrierten Variablen hinzugefügt. Die Koeffizienten für Wert und Erwartung sind nicht signifikant und der Produktterm ist positiv und höchst signifikant (\(\beta=0.20; p=0.000\)). Die Varianzaufklärung dieses Modells beträgt \(R^2=0.89\).
Im dritten Modell wurde der Produktterm der mittelwert-zentrierten Variablen hinzugefügt. Alle Koeffizienten sind hoch signifikant und die Varianzaufklärung beträgt ebenfalls \(R^2=0.89\).
Verglichen mit additiven Modell fallen die Schätzungen der non additiven Modelle etwas besser aus.
\[\begin{array}{|c|c|c|c|c|c|} \hline \ & Additiv & & Unzentriert & & Zentriert & \\ \hline \ Term & beta & p & beta & p & beta & p \\ \hline \text{Konstante} & \text{-1.654} & \text{.000} & \text{0.089} & \text{.594} & \text{1.789} & \text{.000} \\ \text{Wert (W)} & \text{0.569} & \text{.000} & \text{ -0.031} & \text{.558} & \text{0.567} & \text{.000} \\ \text{Erwartung (E)} & \text{0.585} & \text{.000} & \text{0.010} & \text{.847} & \text{0.595} & \text{.000}\\ \text{W x E} & \text{/} & \text{/} & \text{0.199} & \text{.000} & \text{0.199} & \text{.000}\\ \hline \ R^2 & \text{0.823} & \text{} & \text{0.888} & \text{} & \text{0.888} & \text{}\\ \hline \end{array}\]
y1 = -1.654 + 0.569*Wert + 0.585*Erwartung
y2 = 0.089 - 0.031*Wert + 0.010*Erwartung + 0.199*Wert*Erwartung
y3 = 1.789 + 0.567*(Wert-mean(Wert)) + 0.595*(Erwartung-mean(Erwartung)) + 0.199*(Wert-mean(Wert))*(Erwartung-mean(Erwartung))
plot(Motivation, y1, col = "blue", ylim = range(-1, max(y1)+1), xlab = "Wahre Motivation", ylab = "Schätzungen der Motivation", main = "Wahre Werte und Modellschätzungen")
points(Motivation, y2, col = "red")
legend("topleft", legend = c("Additiv", "Non additiv"), col = c("blue", "red"), pch = c(16, 18), lty = 2)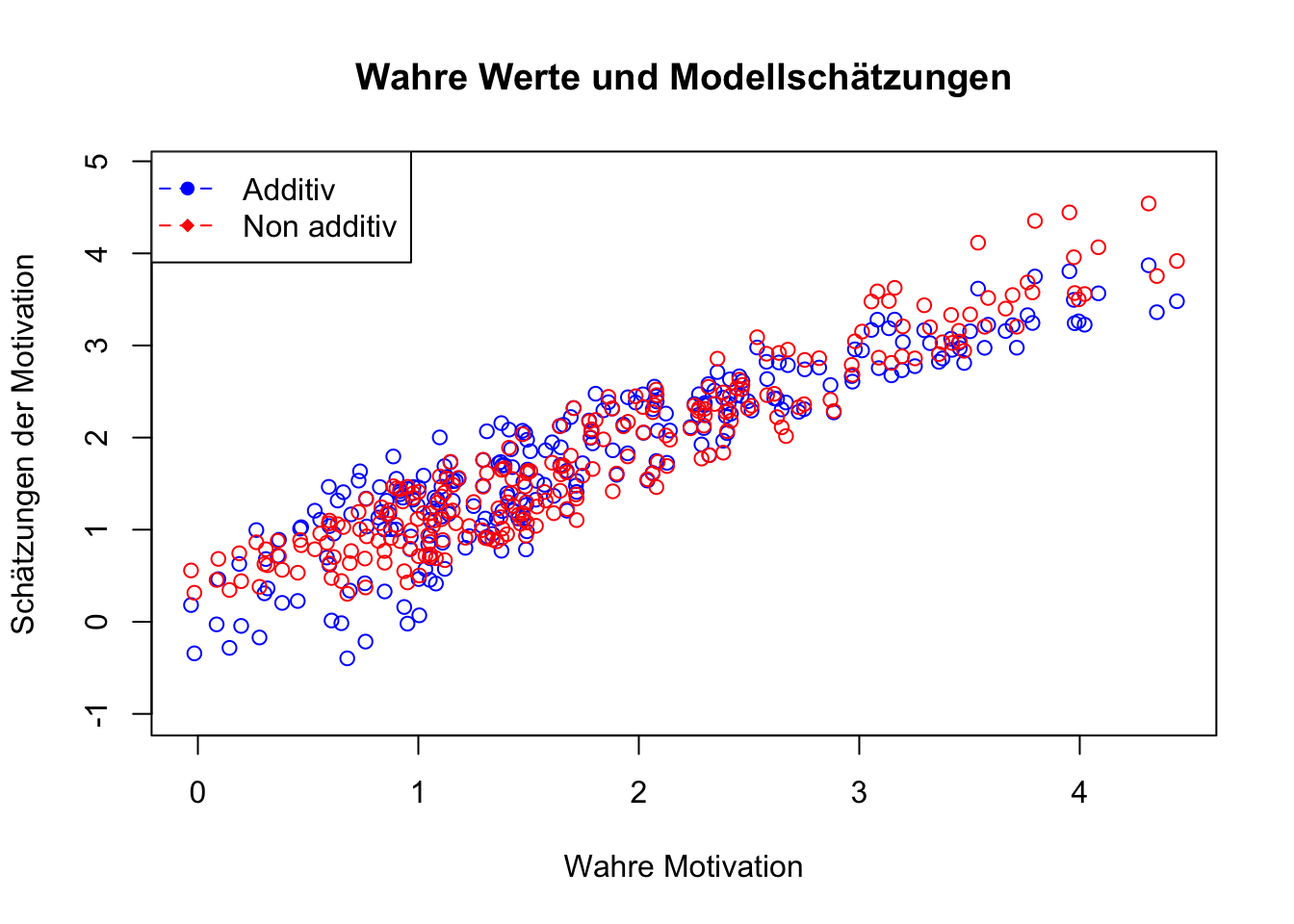
Dabei spielt es keine Rolle, ob unzentrierte oder zentrierte Produktterme verwendet werden. Die Prognosen aus beiden non-additiven Modellen sind trotz unterschiedlicher Koeffizienten absolut identisch. Während die Prognosen für Motivation in beiden Varianten der Produktbildung identisch sind, könnte die Interpretation der Koeffizienten hinsichtlich ihrer Signifikanz unterschiedliche Aussagen zulassen.
# Plot erstellen
plot(y2, y3, col = "black", ylim = range(0, max(y3)), xlab = "Geschätzte Motivation (unzentriert)", ylab = "Geschätzte Motivation (zentriert)", main = "Non-additive Modellschätzungen")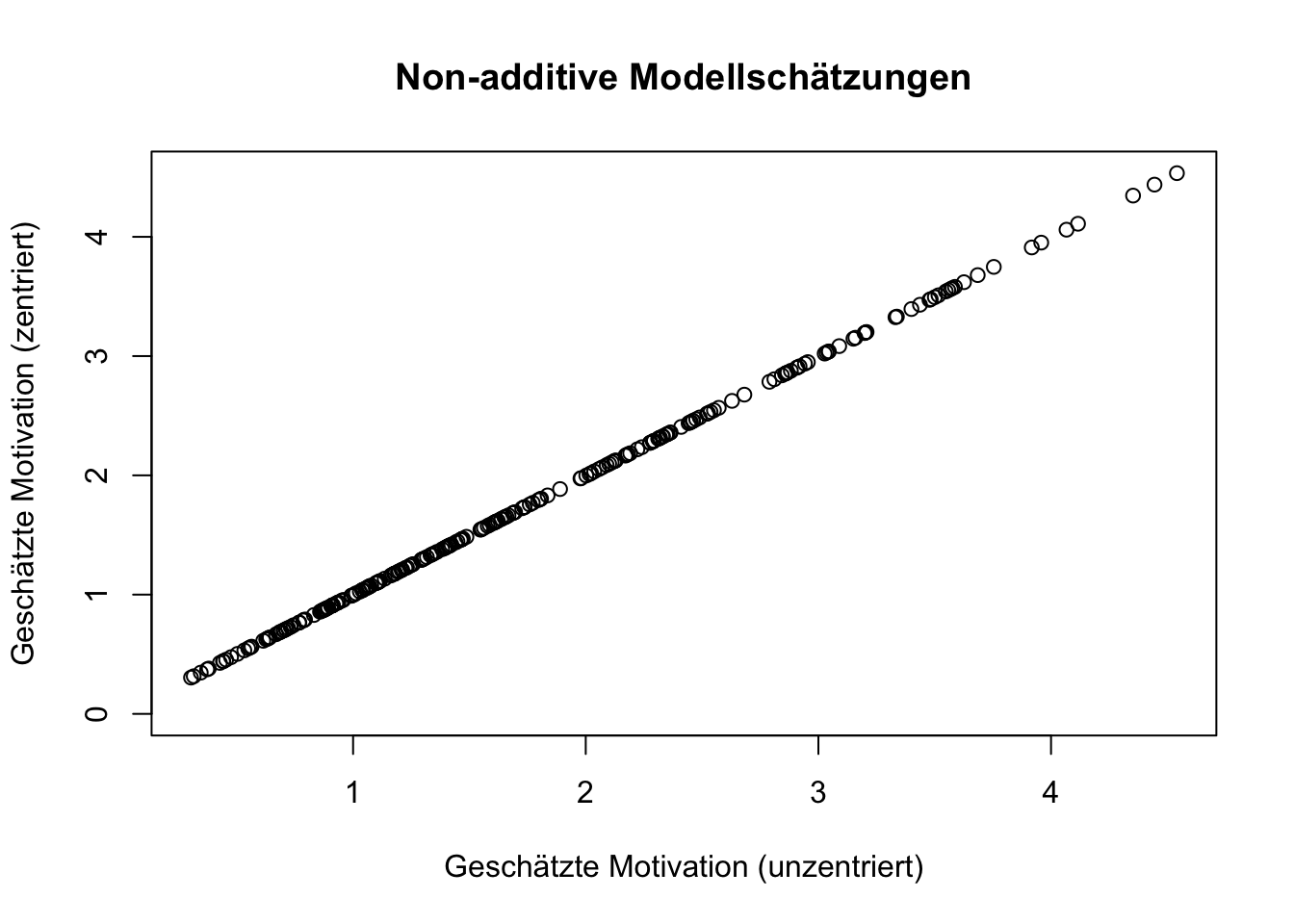
Im Falle der Hypothesentestung mittels Koeffizientenschätzungen, würde das Modell mit mittelwertzentriertem Produktterm eine Substitution nahelegen, d.h. Wert, Erwartung oder Wert und Erwartung gehen mit hoher Motivation einher. Tatsächlich liegt aber eine ausschließlich komplementäre Bedingung vor, d.h. nur wenn Wert und Erwartung hoch ausgeprägt sind, ist die Motivation stark.
Die Annahme oder Zurückweisung von Hypothesen kann also nicht auf Grundlage der signifikanten Koeffizienten im Regressionsmodell basieren, sondern ausschließlich auf der Grundlage der Modellschätzungen für Motivation unter verschiedenen Ausprägungen von Wert und Erwartung. Die folgenden Abbildungen zeigen die identischen Schätzungen für Motivation; links aus Modell 2 (unzentriert) und rechts aus Modell 3 (zentriert). Bei hohem Wert und geringer Erwartung wird eine Motivation von etwa 1.9 geschätzt. Etwa der gleiche Betrag wäre zu erwarten, wenn ein geringer Wert und eine hohe Erwartung vorliegen. Nur wenn Wert und Erwartung hoch ausgeprägt sind, werden Beträge über dem Mittelwert von 2.25 vorausgesagt.
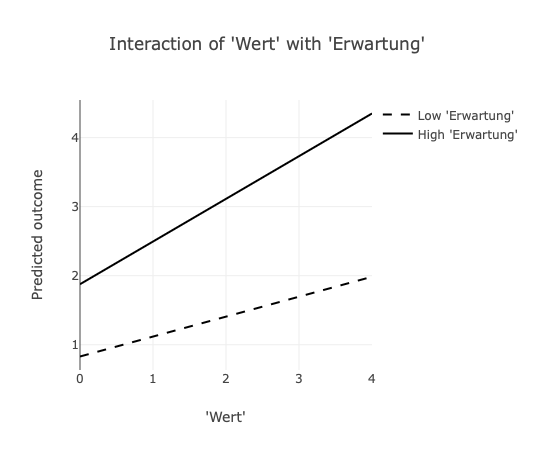
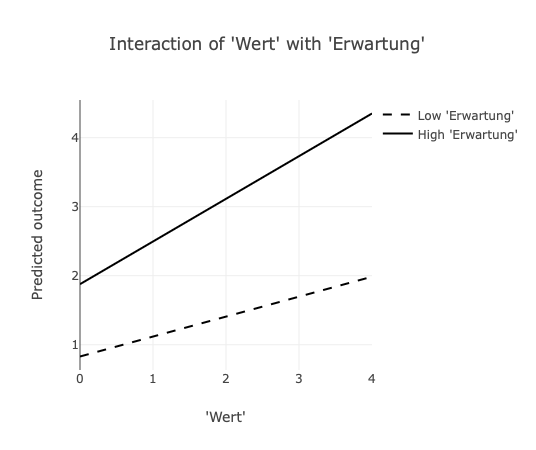
Diese Überlegung lässt sich auf alle Modelle übertragen, in denen eine Zentrierung vorgenommen wird oder die Variablen aus anderen Gründen einen Mittelwert von Null aufweisen (z.B. Faktorwerte). Allgemein lassen sich Regressionsmodelle mit Interaktionsterme durch drei Gleichungen untersuchen:
Unzentrierte Lösung \[\hat{y_i}=\beta_0 +\beta_1 x_i + \beta_2 z_i + \beta_3 x_i z_i +\varepsilon_i\] Zentrierung nur im Produkt \[\hat{y_i}=\beta_0 +\beta_1 x_i + \beta_2 z_i + \beta_3 (x_i-\bar{x}) (z_i-\bar{z}) +\varepsilon_i\]
Zentrierung in Prädiktoren und Produkt \[\hat{y_i}=\beta_0 +\beta_1 (x_i-\bar{x}) + \beta_2 (z_i-\bar{z}) + \beta_3 (x_i-\bar{x}) (z_i-\bar{z}) +\varepsilon_i\]
Jede dieser Schätzfunktionen hat ihre Berechtigung und Anwendbarkeit. Die richtige Darstellung der Ergebnisse aus solchen Regressionsmodellen erfordert jedoch die entsprechende Berechnung in den geschätzen Werte. Eine einfache Lösung findet sich unter https://www.raum-und-zeitlos.de/2wayplot.html. Dabei können die Koeffizienten aus allen drei Varianten verwendet werden, solange die Mittelwerte und Standardabweichungen der Daten in die Eingabemaske richtig eingetragen werden. Wird die Regression nach der zweiten oder dritten Gleichungen durchgeführt, bedarf es im Optionsfeld “Variables X and Z in the product term are:” der Einstellung “Mean-Centred”.
6.3.1.1 Symmetrie
Im Abschnitt Interpretationen wurden vier grundlegende Formen des “Zuwammenwirkens” dargestellt: der AND-Operator im Zusammenhang mit Komplementarität, der NAND-Operator als Exklusion, der OR-Operator als Substitution und der NOR-Operator als Negation.
Im Folgenden wird Symmetrie als Ausrichtung (Alignment) in struktureller Äquivalenz dargestellt, die auf die Situation verweist, in welcher ein Ergebnis nur dann zustande kommt, wenn zwei Bedingungen die gleiche Ausprägung, also den gleichen Wahrheitswert, aufweisen.
Strukturelle Äquivalenz bezieht sich auf die Gleichwertigkeit von Bedingungen, Strukturen oder Systemen. Dies kann bedeuten, dass zwei Bedinungen oder Eigenschaften innerhalb einer Strukturen oder eines Systems auf dieselben Ursachen oder dasselbe Ergebnis verweisen.
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix}\]
Im letzten Abschnitt wurde im Zusammenhang mit dem Wert-mal-Erwartung-Modell der Motivation dargestellt, dass die Motivation (als Produkt von Wert und Erwartung) nur dann stark ausgeprägt ist, wenn Wert und Erwartung beide hoch ausgeprägt sind. Diese Annahme macht nur dann Sinn und kann bestätigt werden, wenn die Daten eine unipolare Skalierung aufweisen, d.h. wenn die Daten im Bereich der positiven Zahlen liegen.
Liegt hingegen eine bipolare Skalierung vor, d.h. wenn die Daten sowohl den negativen als auch den positiven Bereich der Zahlen annehmen können, resultiert die paradoxe Situation, nach welcher das Produkt von Wert und Erwartung auch für den Fall eine hohe Motivation aufweist, in dem das Ziel einen geringen Wert hat und die Erwartung gering ausgeprägt ist, dieses Ziel zu erreichen.
\[\begin{array}{|c|c|c|c|} \hline \text{} & \text{Wert} & \text{Erwartung} & \text{Motivation} \\ \hline \text{unipolare Skala} & \text{0} & \text{0} & \text{0} \\ \text{} & \text{1} & \text{0} & \text{0} \\ \text{} & \text{0} & \text{1} & \text{0} \\ \text{} & \text{1} & \text{1} & \text{1} \\ \hline \text{bipolare Skala} & \text{-1} & \text{-1} & \text{1} \\ \text{} & \text{1} & \text{1} & \text{1} \\ \text{} & \text{-1} & \text{1} & \text{-1} \\ \text{} & \text{1} & \text{-1} & \text{-1} \\ \text{} & \text{0} & \text{0} & \text{0} \\ \text{} & \text{0} & \text{-1} & \text{0} \\ \text{} & \text{-1} & \text{0} & \text{0} \\ \text{} & \text{0} & \text{1} & \text{0} \\ \text{} & \text{1} & \text{0} & \text{0} \\ \hline \end{array}\]
Aufgrund der Messung, also der Zuordnung von Zahlen zu einer Aussagenkategorie, resultiert in den Daten eine Logik der Symmetrie. Der Produktterm in Regressionsmodellen indiziert nicht mehr nur die Komplementarität (bei positivem Vorzeichen des Regressionskoeffizienten) oder die Substitution (bei negativem Vorzeichen des Regressionskoeffizienten) von Bedingungen, sondern auch die Symmetrie zweier Bedingungen (bei positiven Vorzeichen) oder die Asymmetrie (bei negativem Vorzeichen).
Symmetrie weist also auch auf Komplementarität hin, weisen die Daten jedoch einen Wertebereich auf, der positive und negative Zahlen einschließt, oder wenn Zentrierungen eingesetzt werden, schließt Symmetrie auch die Situation ein, in welcher die Symmetrie in der Abwesenheit von Merkmalen besteht.
(Einen Sonderfall nimmt die Situation ein, in der beide Bedingungen symmetrisch ausgeprägt sind, aber einen Betrag von Null aufweisen. In dieser Situation ergibt das Produkt trotz Symmetrie einen Betrag von Null.)
Die Wirkung der Symmetrie lässt sich aufzeigen, wenn mittelwertzentrierte Variablen eingesetzt werden. Ein Beispiel für die Symmetrie zweier Bedingungen kann die organisatorische Ambidextrie aufzeigen.
Ambidextrie bezieht sich dabei auf die Fähigkeit oder die Ausrichtung einer Organisation, effizient in ihrem aktuellen Geschäft zu sein (Exploitation) und sich gleichzeitig, z.B. durch Innovation und Anpassung an neue Bedingungen weiterzuentwickeln (Exploration). Während die Exploitation darauf ausgerichtet ist, die bestehenden Fähigkeiten besser auszunutzen, z.B. durch die Optimierung der Prozesse und Technologien, ist die Exploration darauf ausgerichtet, neue Möglichkeiten zu Erkunden.
“The conventional view has been that the drivers of ambidexterity are complements, i.e.they work better when used in combination. […] Harmonic ambidexterity […] refers to the ‘locus’ of ambidexterity […] (a) occurring within a single unit rather than by balancing across units, and (b) occurring at a single point in time rather than by cycling back and forth over time.” (Zimmermann & Jaeckel, 2020, S. 2)
Die folgende Abbildung (links) lässt keinen systematischen Zusammenhang zwischen Exploitation und Exploration erkennen. Das resultiert aus ihrer Definition als unabhängige Zufallsvariablen. Exploitation und Exploration weisen jeweils einen Wertebereich von -2 bis +2 auf. Negative Werte für Exploitation weisen diejenigen Unternehmen auf, deren Ausrichtung auf die Effizienz im aktuellen Geschäft unterduchschnittlich stark ausgeprägt ist. Positive Werte weisen diejenigen Unternehmen auf, deren Ausrichtung auf Effizient stärker ausgeprägt ist. Gleiches gilt für die Ausprägung der Exploration. Unternehmen, die weniger explorieren als andere Unternehmen in der Stichprobe, weisen negative Werte auf und diejenigen Unternehmen, die stärker explorieren als die anderen Unternehmen, weisen positive Werte auf.
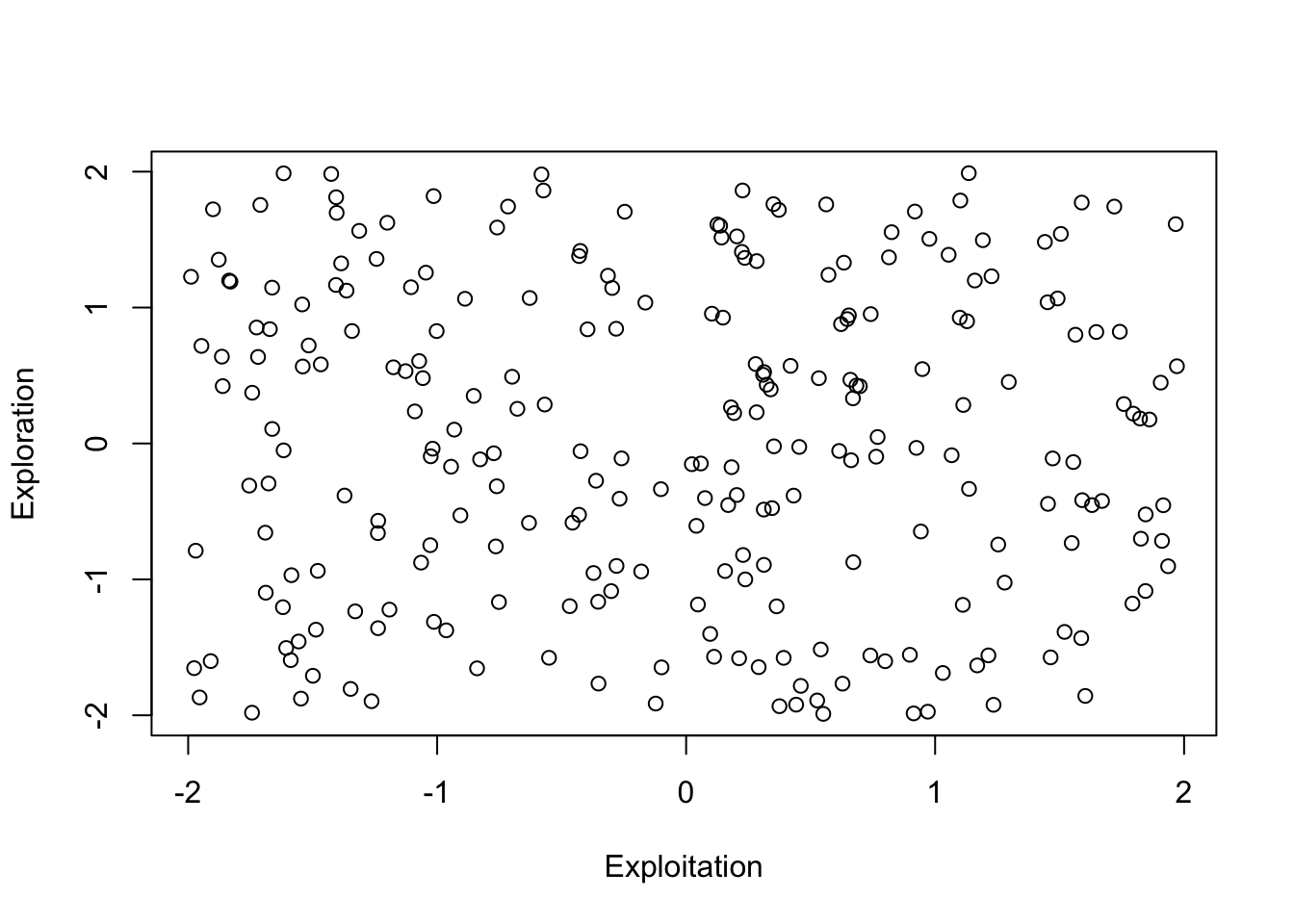
Die Werte für Exploitation und Exploration lassen vier Kategorisierungen zu:
- Unternehmen mit unterdurchschnittlicher Exploitation (<0) und unterdurchschnittlicher Exploration (<0) finden sich im Quadranten links unten
- Unternehmen mit unterdurchschnittlicher Exploitation (<0) und überdurchschnittlicher Exploration (>0) finden sich im Quadranten links oben
- Unternehmen mit überdurchschnittlicher Exploitation (>0) und unterdurchschnittlicher Exploration (<0) finden sich im Quadranten rechts unten
- Unternehmen mit überdurchschnittlicher Exploitation (>0) und überdurchschnittlicher Exploration (>0) finden sich im Quadranten rechts oben
Die harmonische Ambidextrie, im Sinne einer Symmetrie von Exploitation und Exploration findet sich in zwei Kategorien: wenn Exploitation und Exploration gering ausgeprägt sind oder wenn beide hoch ausgeprägt sind.
Werden die Zusammenhänge von Exploitation (links) und Exploration (rechts) mit Ambidextrie (dem Produkt-Term aus Exploitation und Exploration) dargestellt, zeigt sich für beide Fällen ein schleifenartiges Bild.
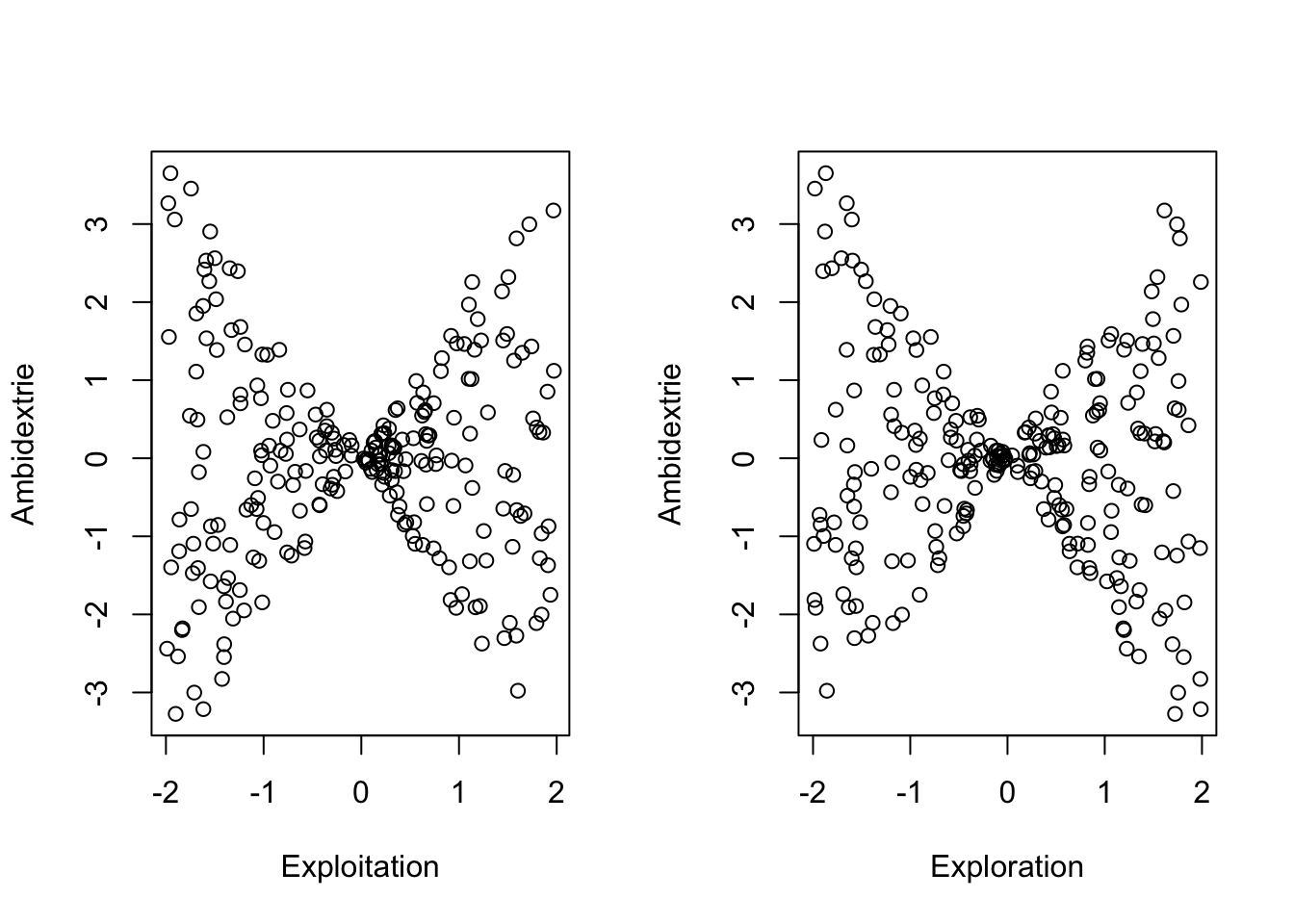
Hohe Ambidextrie kann demnach sowohl für hohe Exploitation, aber auch für geringe Exploitation aufgezeigt werden und dies resultiert aus dem Produkt geringer Exploitation (negative Werte) mit geringer Exploration (negative Werten). Ambidextrie wird in diesem Fall also als Symmetrie bzw. strukturelle Äquivalenz operationalisiert.
Wird die Darstellung nicht zwei-dimensional, sondern drei-dimensional abgebildet und die Perspektive um 45 Grad rotiert, zeigt sich ein sattelförmiger Zusammenhang zwischen Exploitation, Exploration und Ambidextrie. In der vorderen Ecke der räumlichen Darstellung ist Exploitation gering (-2) und Exploration hoch (+2) ausgeprägt. Diese Asymmetrie geht mit einer geringen Ambidextrie einher. In der hinteren (gegenüberliegenden) Ecke, die hier nicht sichtbar ist, wird ebenfalls geringe Ambidextrie vorgefunden. Wenn Exploitation und Exploration beide gering (-2) ausgeprägt (linke Ecke) oder beide sind hoch (+2) ausgeprägt (rechts) liegt eine hohe Ambidextrie vor.
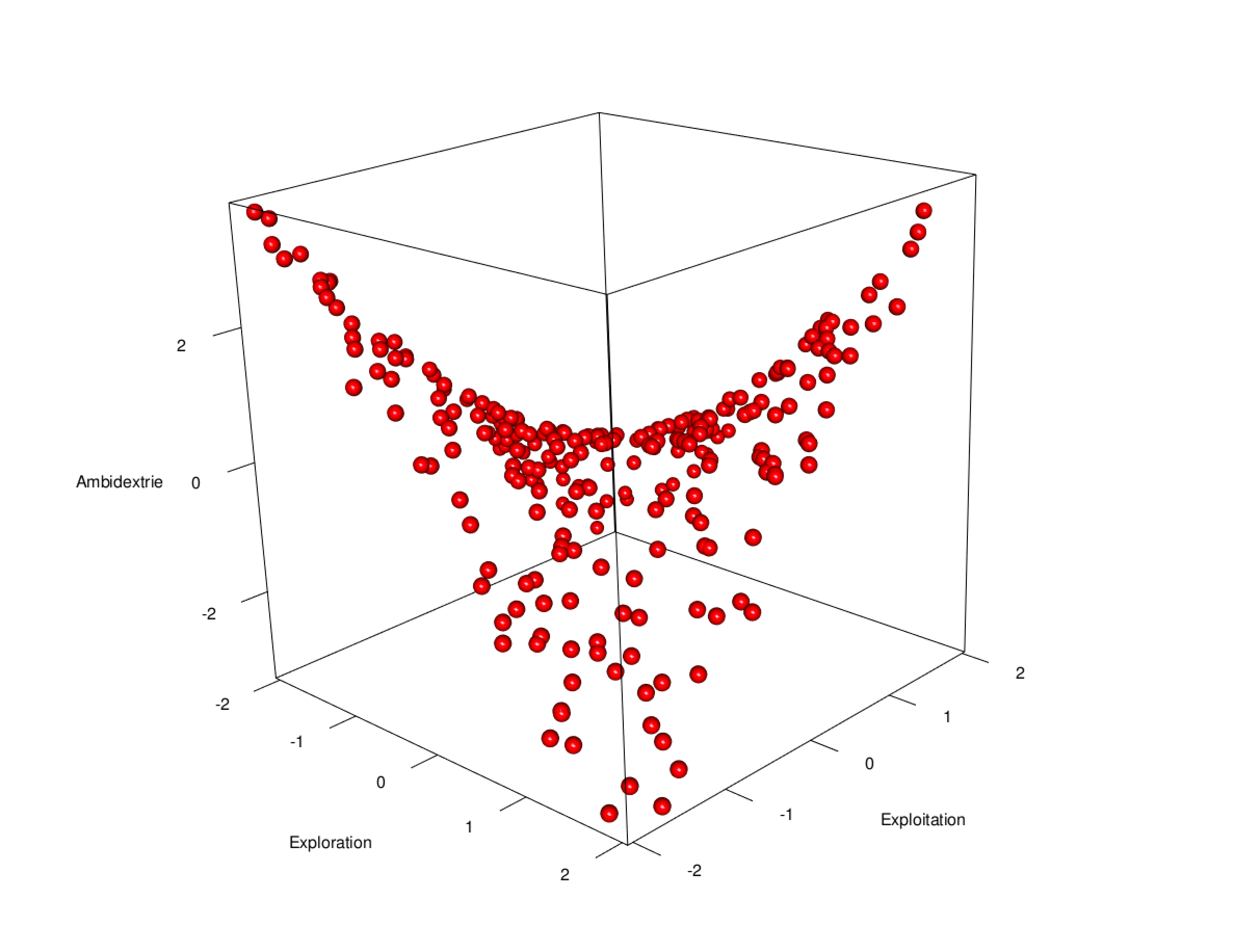
Um Missverständnissen vorzubeugen, sei hier einmal darauf verwiesen, dass hier kein Ergebnis in der Weise dargestellt wird, dass Unternehmen mit geringer Exploration und geringer Exploitation die Vorteile aus Ambidextrie beziehen.
Es handelt sich vielmehr um eine mögliche Operationalisierung von Ambidextrie, die bewusst eingesetzt werden kann, um Symmetrie von Exploitation und Exploration zu beforschen, die aber auch aus dem Skalenformat resultieren kann.
Die folgende Abbildung zeigt auf, wie die Ambidextrie mit dem Unternehmenserfolg assoziiert ist. Aufgrund der Operationalisierung von Ambidextrie als symmetrische Ausprägung von Exploitation und Exploration wird Ambidextrie in der Regressionsanalyse gegenüber der Bedingung untersucht, dass keine symmetrische Ausprägung vorliegt, also entweder Exploitation oder Exploration dominiert.
# 3D-Diagramm erstellen
# library(rgl)
# plot3d(Exploitation, Ambidextrie , Exploration, type = "s", col = "red", size = 1)
plot (Ambidextrie, Unternehmenserfolg, xlab="Ambidextrie als Ausrichtung von Exploitation und Exploration)", ylab= "Unternehmenserfolg")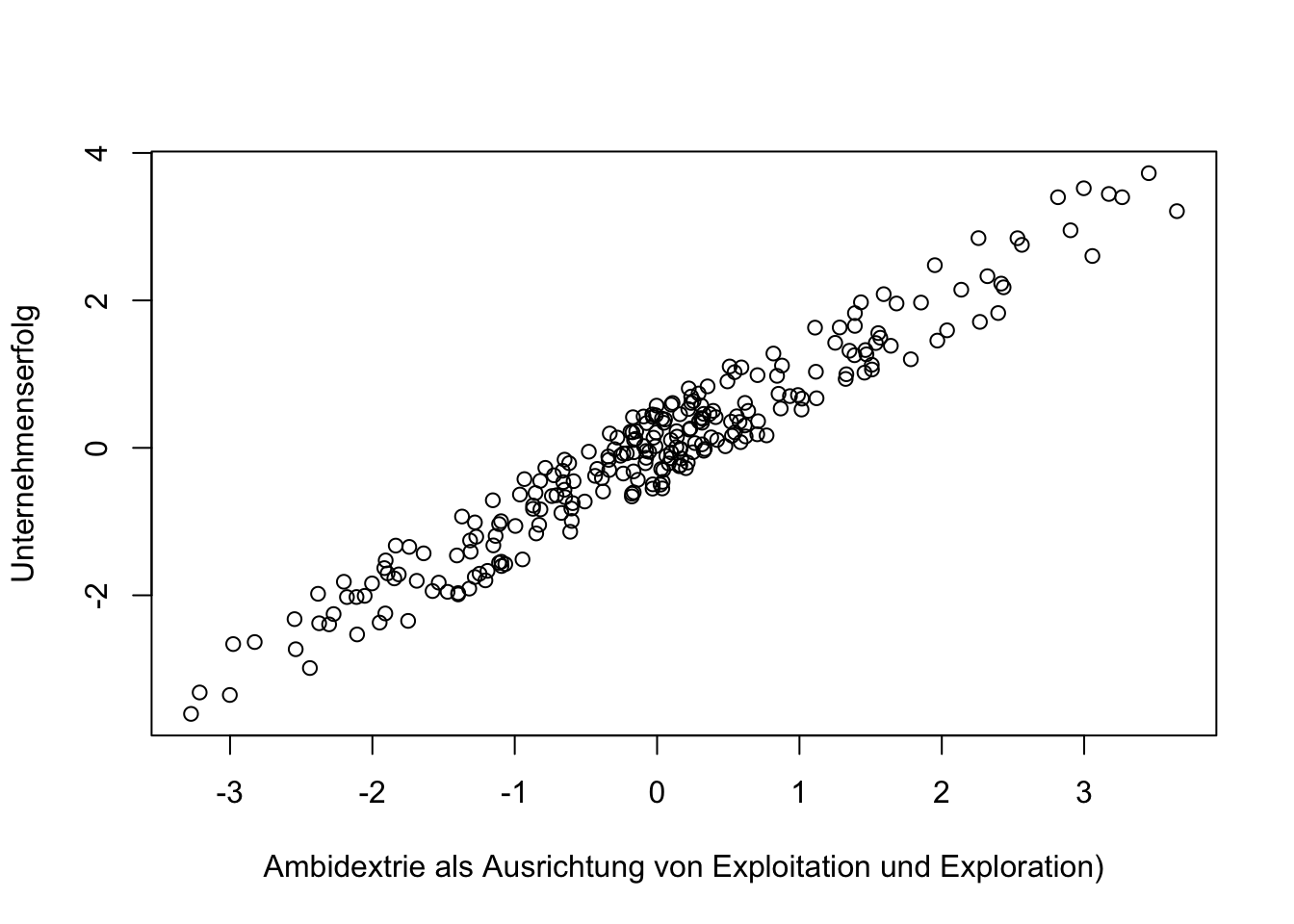
Ambidextrie = Exploitation * Exploration
summary(lm(Unternehmenserfolg ~ Exploitation + Exploration + Ambidextrie))##
## Call:
## lm(formula = Unternehmenserfolg ~ Exploitation + Exploration +
## Ambidextrie)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.65543 -0.29543 0.01755 0.27876 0.61172
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.013988 0.021561 -0.649 0.5171
## Exploitation 0.035103 0.018987 1.849 0.0657 .
## Exploration -0.006263 0.018792 -0.333 0.7392
## Ambidextrie 1.001227 0.016574 60.408 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3404 on 246 degrees of freedom
## Multiple R-squared: 0.9376, Adjusted R-squared: 0.9369
## F-statistic: 1232 on 3 and 246 DF, p-value: < 2.2e-16Der signifikant positive Koeffizient von Ambidextrie bestätigt den Interaktionseffekt von Exploitation und Exploration (Ambidextrie). Ambidextrie ist demnach positiv mit dem Unternehmenserfolg assoziiert und dabei ist es unerheblich, ob Exploitation und Exploration gering oder hoch ausgeprägt sind. Das Ergebnis weist darauf hin, dass die Ambidextrie als Balance von Exploitation und Exploration, gegenüber der Dominanz von Exploitation oder Exploration, von Vorteil ist.
In der Abbildung wird deutlich, dass ein hoher Unternehmenserfolg in zwei Situationen vorgefunden wird.
Die gestrichelte Linie zeigt auf, wie hoch der Unternehmenserfolg geschätzt wird, wenn Unternehmen wenig explorieren. Hier zeigt sich ein hoher Unetrnehmenserfolg, wenn wenig Exploitation vorliegt (links). Mit steigender Exploitation, was gegen die Operationalisierung durch Symmetrie verläuft, wird der zu erwartende Unternehmenserfolg geringer.
Die durchgezogene Linie zeigt auf, wie hoch der Unternehmenserfolg geschätzt wird, wenn Unternehmen viel explorieren. Hier zeigt sich der höchste Unternehmenserfolg für den Fall, dass Exploitation ebenfalls hoch ausgeprägt ist (rechts)
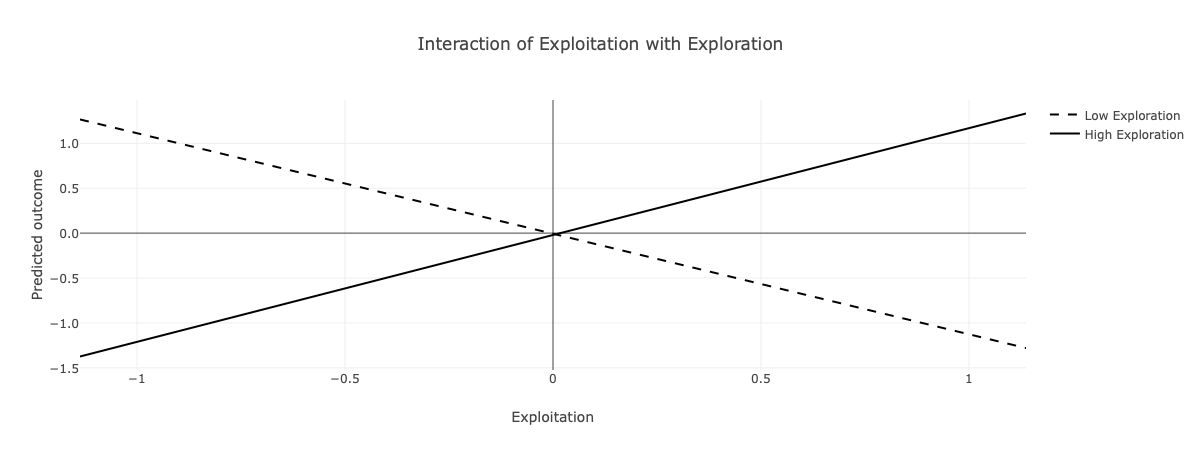
6.3.1.2 Asymmetrie
Asymmetrie wird im Folgenden als strukturelle Kontravalenz dargestellt, die auf die Situation verweist, in welcher ein Ergebnis nur dann zustande kommt, wenn zwei Bedingungen die entgegengesetzte Ausprägung, also den umgekehrten Wahrheitswert, aufweisen.
Die strukturelle Kontravalenz ist ein Konzept, dass sich auf die Ungleichwertigkeit von Bedingungen Strukturen oder Systemen bezieht. Dies kann bedeuten, dass das Vorhandensein von Gegensätzen innerhalb eines Systems oder einer Struktur, zusammen eine ausgewogene oder funktionale Einheit bildet. In sozialen Strukturen können Hierarchien kontravalente Beziehungen aufweisen. Beispielsweise können die Rollen von Führungskräften und Mitarbeitern als kontravalent betrachtet werden, da sie unterschiedliche, aber komplementäre Funktionen innerhalb eines Unternehmens erfüllen.
\[\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix}\begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}\]
Asymmetrie kann also nicht nur auf Fehlausrichtung (Mis-Alignment) hinweisen, sondern auf Situationen hinweisen, in denen ein Ergebnis durch die Asymmetrie von Bedingungen entsteht. So kann die Unternehmensleitung nur dann entscheiden und führen, wenn Mitarbeiter da sind, die sich führen lassen. Durch die Asymmetrie im Führungsanspruch (Dominanz) entsteht ein funktionierendes System.
Die Wirkung der asymmetrischen Ausrichtung lässt sich aufzeigen, wenn mittelwertzentrierte Variablen eingesetzt werden. Die Umsetzung folgt der symmetrischen Ausrichtung. Im Unterschied dazu weist ein negativer Koeffizienten des Interaktionsterms auf den Vorteil eines asymmetrischen Wirkens hin.
6.3.2 Kalibrierung
Wenn Daten mit symmetrischer Skalierung oder zentrierte Daten vorliegen, die Produkt-Terme dieser Daten in Regressionsmodellen verwendet werden und die Effekte struktureller Äquivalenz (Symmetrie) oder Kontravalenz (Asymmetrie) unerwünscht sind, dann können diese Daten kalibriert werden. Ich verwende hier den Begriff Kalibrierung, weil er durch die Fuzzy-Set-Qualitative Comparative Analyse (fsQCA) bekannt ist, wenn mengentheoretische Aussagen aus Daten analysiert werden.
Mit der Kalibrierung wird hier eine Möglichkeit aufgezeigt, die eine logistische Transformation von empirischen Daten in “Mitgliedschaftsgrade” bzw. Wahrscheinlichkeiten (ich bevorzuge letzteres) werden kann, um die inhaltliche Analyse von Daten zu vereinfachen und Fehlinterpretationen in Regressionsmodellen, insbesondere mit Produkt-Termen, zu reduzieren.
Die Methode der Kalibrierung basiert auf dem Konzept der Wahrscheinlichkeit und die damit verbundene probabilistische Theorie wird für eine Reihe von Wahrnehmungs-, Bewertungs- oder Entscheidungsprozessen als nützlich angesehen. Auch bei der Modellierung künstlicher neuronaler Netzwerke wird diese Methode eingesetzt, da sie ein mathematisches Modell bietet, dass den Prozessen bei der Aktivierung von Nervenzellen im Gehirn nahe kommt.
Die Wahrscheinlichkeit für ein Merkmal (z.B. die Aktivierung eines künstlichen Neurons oder die Entscheidung für Zustimmung zu einer Aussage) folgt dabei einer monoton steigenden Funktion und entspricht in vielen Fällen dem S-förmigen Verlauf der logistischen Funktion (auch Sigmoid-Funktion genannt)
Diese Funktion hat die allgemeine Gleichung:
\[f(x)=\frac{1}{1+exp(-x)}\]
Im folgenden Beispiel reicht der Wertebereich der Variable \(X\) von -5 bis +5. Im Histogramm (links) wird deutlich, dass die Werte einer Normalverteilung folgen. Rechts wird die logistische Funktion von \(X\) dargestellt.
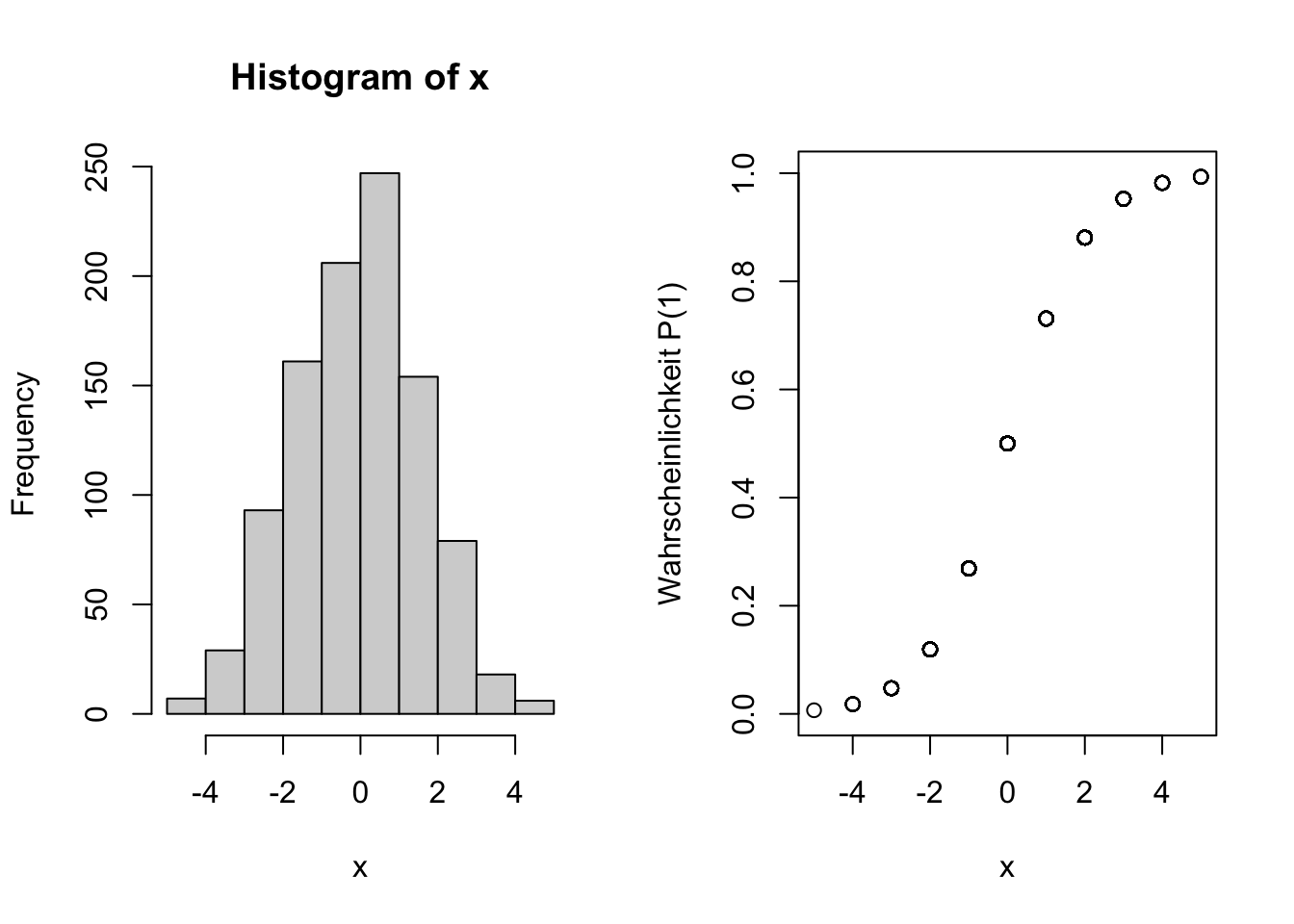
Die logistische Funktion interpretiert \(Y\) als Wahrscheinlichkeit, die Werte im Bereich von 0 bis 1 annehmen kann. Es wird deutlich, dass eine Wahrscheinlichkeit von \(P=0.5\) (entspricht 50 %) einem Wert von \(X=0\) zugeordnet ist. Mit anderen Worten entspricht der Stichprobendurchschnitt (X=0) einer Wahrscheinlichkeit von 50 Prozent, dass eine Antwort zutrifft oder ein Merkmal gegeben ist.
Die Werte im bereich \(X<-6\) sind mit einer Wahrscheinlichkeit von \(P=0.0\) assoziiert, während Werte im Bereich \(X>6\) mit einer Wahrscheinlichkeit von p=1.0 verbunden sind.
Wird eine fünfstufige Ratingskala (mit Werten von 1 bis 5) in die logistische Funktion transformiert, resultiert die Wahrscheinlichkeitsfunktion, welche die Wahrscheinlichkeit für die Zustimmung in Abhängigkeit von der Intensität der Zustimmung widerspiegelt.
Dabei wird zwischen der theoretischen und der empirischen Wahrscheinlichkeitsfunktion unterschieden.
Empirische Wahrscheinlichkeitsfunktion
Im folgenden Beispiel werden die symmetrischen Skalen (Wertebereich von -2 bis +2) von Exploitation und Exploration in logistische Funktionen transformiert.
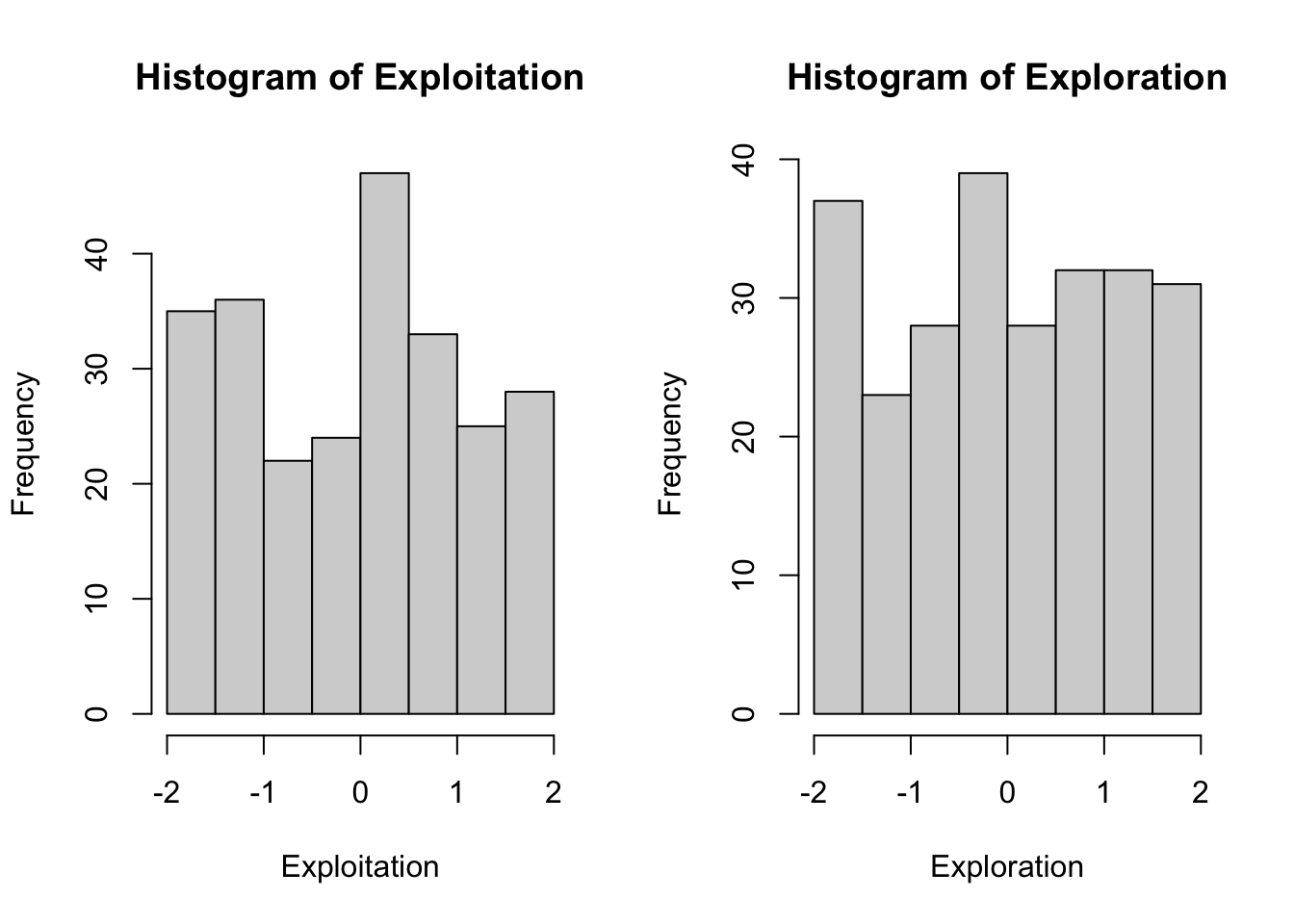
Der Erwartungswert \(\alpha\) der logistischen Verteilungen ergibt sich jeweilige aus dem Median der Häufigkeitsverteilung von Exploitation und Exploration.
Die Varianz von Exploitation bzw. Exploration entscheidet jeweils über die Steilheit (\(\beta\)) der logistischen Verteilung.
\[var(x)=\frac {\beta^2 \pi^2}{3}\] umgestellt nach \(\beta\) ergibt sich: \[ \beta = \sqrt {\frac{var(x)*3}{\pi^2}}\]
Die Verteilungsfunktion für Zustimmung (X=1) ergibt sich dann aus:
\[p(X=1)=f(x)=\frac {1}{1+e^{-\frac{x-\alpha}{\beta}}}\]
Die eulersche Zahl \(e\) entspricht in der Schreibweise von R der Anweisung: exp(1), wobei der Ausdruck: \(e^x\) der Schreibweise exp(x) bzw. \(e^{-x}\) als exp(-x) ausgedrückt wird.
par(mfrow=c(1,2))
p_exploi=1/(1+exp(-((Exploitation-alpha_exploi)/beta_exploi)))
plot (Exploitation,p_exploi, ylab=("P(Exploitation)"))
p_explor=1/(1+exp(-((Exploration-alpha_explor)/beta_explor)))
plot (Exploration,p_explor, ylab=("P(Explortation)"))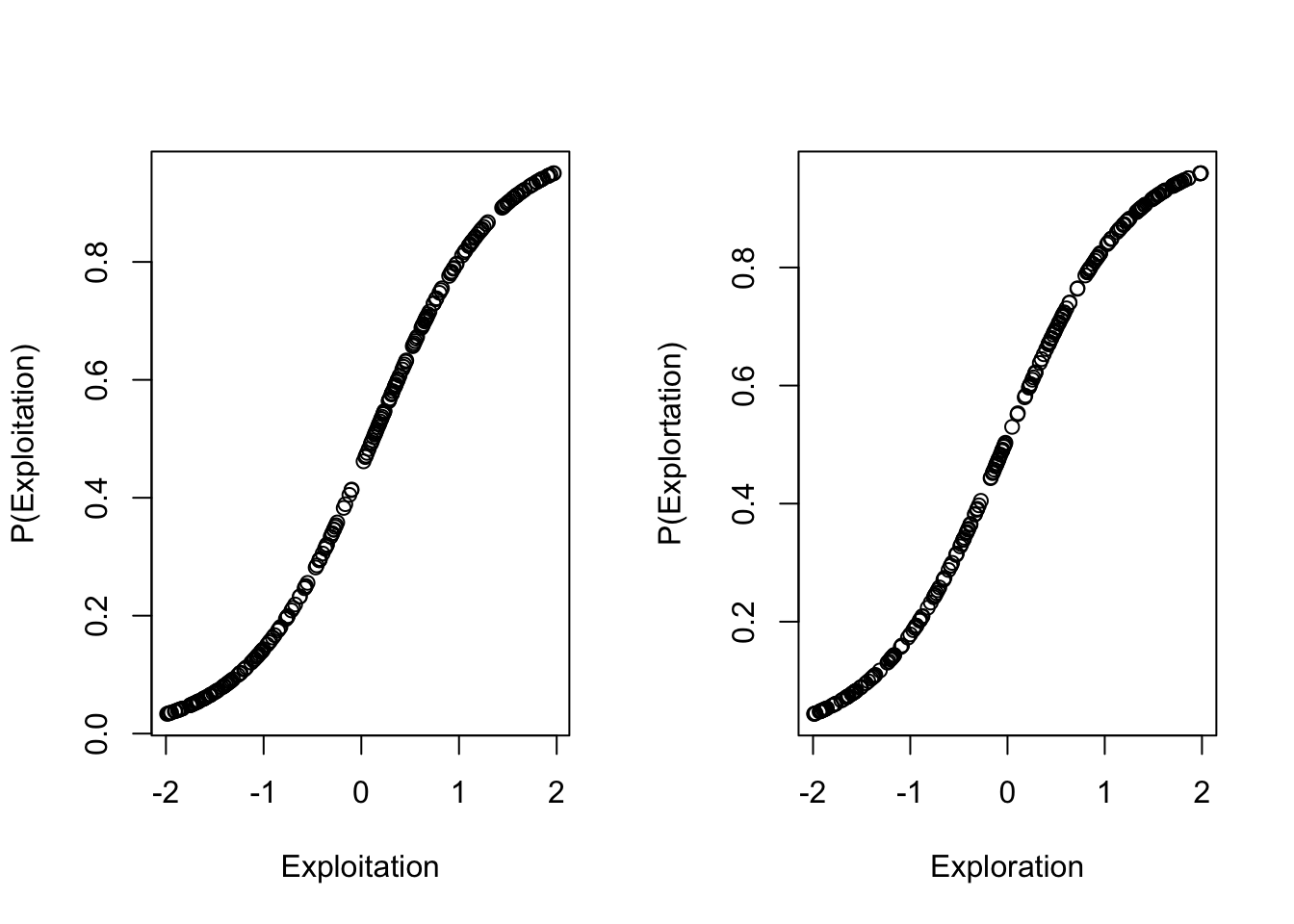
## Exploitation p_exploi Exploration p_explor
## 1 0.9427855 0.7882955 -0.6475744 0.27436856
## 2 0.4316726 0.6222368 -0.3836656 0.36409578
## 3 1.1131698 0.8301343 0.2833129 0.62035312
## 4 -0.7605798 0.1972565 -0.3150049 0.38943757
## 5 0.9137679 0.7804646 -1.9860405 0.04406535
## 6 0.5264156 0.6570652 -1.8910300 0.05080437Dem Wert von \(X=0.94\) in Zeile 1 ist hier eine Wahrscheinlichkeit für die Zustimmung zur Exploitation in Höhe von \(p=0.79\) zugewiesen. Die Gegenwahrscheinlichkeit, also die Wahrscheinlichkeit, dass dieser Wert \(X=0.94\) keine Zustimmung ausdrückt ergibt sich aus:
\[p(0)=1-p(1)\] Odds-Ratio
Hat man für ein Ereignis \(E\) die Wahrscheinlichkeit und die Gegenwahrscheinlichkeit, kann man die sogenannten Odds bestimmen. Odds (bzw.Chancen) bezeichnen die Wahrscheinlichkeit (eines Ereignisses) im Verhältnis zu ihrer Gegenwahrscheinlichkeit. In diesem Fall ergeben sie sich aus:
\[ Odds (E) = \frac {p(E)}{p(\neg{E})} = \frac {p(1)}{1-p(1)} = Odds \: ratio\]
Log Odds
Die Log Odds ergeben sich aus dem natürlichen Logarhytmus der Odds als:
\[ Log\: Odds = ln (Odds)\] Die Log-Odds weisen eine symetrische Verteilung um den Wert Null auf und sind (wie Zentrierungen) für einige Analysen von Vorteil.
## Exploitation p_exploi Exploration p_explor odds logodds
## 1 0.9427855 0.7882955 -0.6475744 0.27436856 3.7235655 1.3146817
## 2 0.4316726 0.6222368 -0.3836656 0.36409578 1.6471611 0.4990533
## 3 1.1131698 0.8301343 0.2833129 0.62035312 4.8870032 1.5865793
## 4 -0.7605798 0.1972565 -0.3150049 0.38943757 0.2457279 -1.4035304
## 5 0.9137679 0.7804646 -1.9860405 0.04406535 3.5550736 1.2683758
## 6 0.5264156 0.6570652 -1.8910300 0.05080437 1.9160065 0.6502431Theoretische Wahrscheinlichkeitsfunktion
Übertragen auf eine typische Ratingskala sind die Werte mit den semantischen Ankerpunkten “1 - stimme nicht zu” vs. “5 -stimme vollständig zu” und mit einem Skalenmittelpunkt von “3 - teils/teils” assoziiert und respräsentieren die theoretischen Ankerpunkte für keine Zustimmung (x=1), Schwellenwert (x=3) und Zustimmung (x=5).
Als theoretischen Erwartungswert \(\alpha\) der logistischen Verteilung wird in diesem Fall der Schwellenwert zugewiesen. D.h. dies ist der am häufigsten (50%) erwartete Wert von \(x\).
Grundsätzlich liegt hier eine Entscheidung zwischen “keiner Zustimmung” und “Zustimmung” vor. Die Wahrscheinlichkeit für Zustimmung steigt mit höher ausgeprägter Bewertung der Skala und erreicht bei dem Wert “5” ihr Maximum (p=1).
Wenn dem Wert “5” eine Wahrscheinlichkeit von p=1 entspricht, kann entsprechend:
\[ Odds (x=5) = \frac {1}{(1-1)} = \frac {1}{0} = n.l.\]
nicht bestimmt werden. Wird aus pragmatischen Gründen die Wahrscheinlichkeit für p=0.9999 festgelegt, resultieren \(Odd=9.999\) und \(Log\: Odd=2.302\).
Die Wahrscheinlichkeit p(E) bzw. der Grad der Mitgliedschaft (Degree of Membership; DoM) der Werte \(x_i\) lässt sich in einem Schritt ermitteln Dușa (2024) durch:
\[DoM(i) = x_{calib} = \frac {1}{1+e^{-\frac{(x_i-cp) \: \cdot \: (log \:odd_{fi})}{fi-cp}}}\]
wobei \(x_i\) den Rohwert, \(cp=3\) den Schwellenwert (crossover-point) und \(fi=5\) den Wert “vollen Einschlusses” (Zustimmung) darstellen.
x=example$Exploitation
cp=median(x)
odd_fi=10 # 9.999
fi=2
example$DoM_exploi=1 / (1 + exp(-((x-cp)*(log(odd_fi))/(fi-cp))))Bei der Kalibrierung, wie sie von Ragin (2008) vorgestellt wird, handelt es sich um ein Verfahren, mit dem sich Intervallskalen oder metrische Daten (z.B. Faktorwerte) in Wahrscheinlichkeitsfunktionen umformen lassen. Ein entscheidender Vorteil besteht in der Möglichkeit, Wahrscheinlichkeiten zu kombinieren.
Unter der Annahme, dass zwei Ereignisse A und B (z.B. Exploitation und Exploration) stochastisch unabhängig sind, ergibt sich die Wahrscheinlichkeit, dass beide Ereignisse zugleich eintreten (als Schnittmenge) aus dem Produkt ihrer Wahrscheinlichkeiten (Bortz, 1993, S. 55).
\[P(A \cap B)= P(A) \cdot P(B)\]
Bei der Methode der Kalibrierung ergibt sich der Grad der Zustimmung (membership) nach Ragin (2008) aus:
\[odd_{membership}= \frac{degree \:of \: membership}{1-(degree \: of \: membership)}\] wobei die direkte Kalibrierungsmethode einschließt, dass:
\[ degree \: of \:membership = \frac {exp(log \:odds)}{1+exp(log \:odds)}\]
wobei “exp” das Exponential der log odds im Verhältnis zu den einfachen odds darstellt Ragin (2008).
## Loading required package: admisc##
## To cite package QCA in publications, please use:
## Dusa, Adrian (2019) QCA with R. A Comprehensive Resource.
## Springer International Publishing.
##
## To run the graphical user interface, use: runGUI()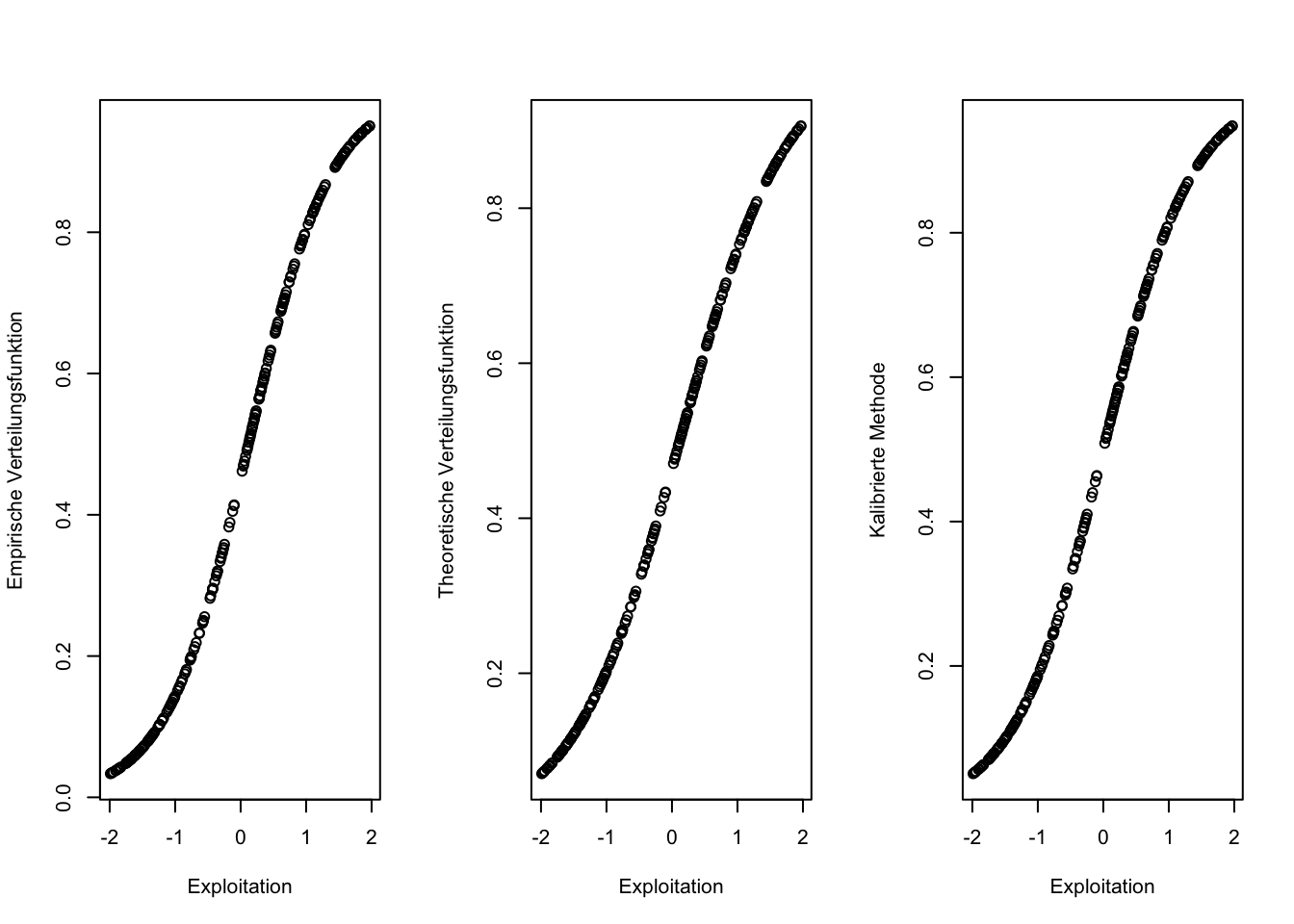
## Exploitation p_exploi Exploration p_explor odds logodds
## Exploitation 1.00 0.99 -0.02 -0.03 0.79 1.00
## p_exploi 0.99 1.00 -0.03 -0.02 0.76 0.99
## Exploration -0.02 -0.03 1.00 0.99 -0.01 -0.02
## p_explor -0.03 -0.02 0.99 1.00 -0.02 -0.03
## odds 0.79 0.76 -0.01 -0.02 1.00 0.79
## logodds 1.00 0.99 -0.02 -0.03 0.79 1.00
## DoM_exploi 1.00 1.00 -0.03 -0.03 0.77 1.00
## Exploitation_c 0.99 1.00 -0.03 -0.03 0.75 0.99
## DoM_exploi Exploitation_c
## Exploitation 1.00 0.99
## p_exploi 1.00 1.00
## Exploration -0.03 -0.03
## p_explor -0.03 -0.03
## odds 0.77 0.75
## logodds 1.00 0.99
## DoM_exploi 1.00 1.00
## Exploitation_c 1.00 1.00In diesem Fall stimmt die empirische Verteilungsfunktion (p_1_exploi) mit der theoretischen Verteilungsfunktion (Degree of membership - DoM) und mit den im QCA-Package bestimmten kalibrierten Werte (x_cbr) bis auf geringe Abweichungen überein. Bei nicht-normalverteilten Daten, würden die Werte der empirischen Verteilungsfunktion stärker abweichen.
Ein Vorteil der Transformation in Wahrscheinlichkeiten ergibt sich aus der Möglichkeit ihrer Kombination. Aus der Eigenschaft von Wahrscheinlichkeiten, dass sie einen Wert \(0 \to 1\) annehmen, kann die Wahrscheinlichkeit der Ambidextrie aus dem Produkt der Wahrscheinlichkeit für Exploitation und der Wahrscheinlichkeit für Exploration bestimmt werden.
\[p(Ambidextrie) = p(Exploitation) \cdot p(Exploration)\]
Ambidextrie_log=p_exploi*p_explor
par(mfrow=c(1,2))
plot(p_exploi, Ambidextrie_log, xlab="p(Exploitation)", ylab="p(Ambidextrie)")
plot(p_explor, Ambidextrie_log, xlab="p(Exploration)", ylab="p(Ambidextrie)")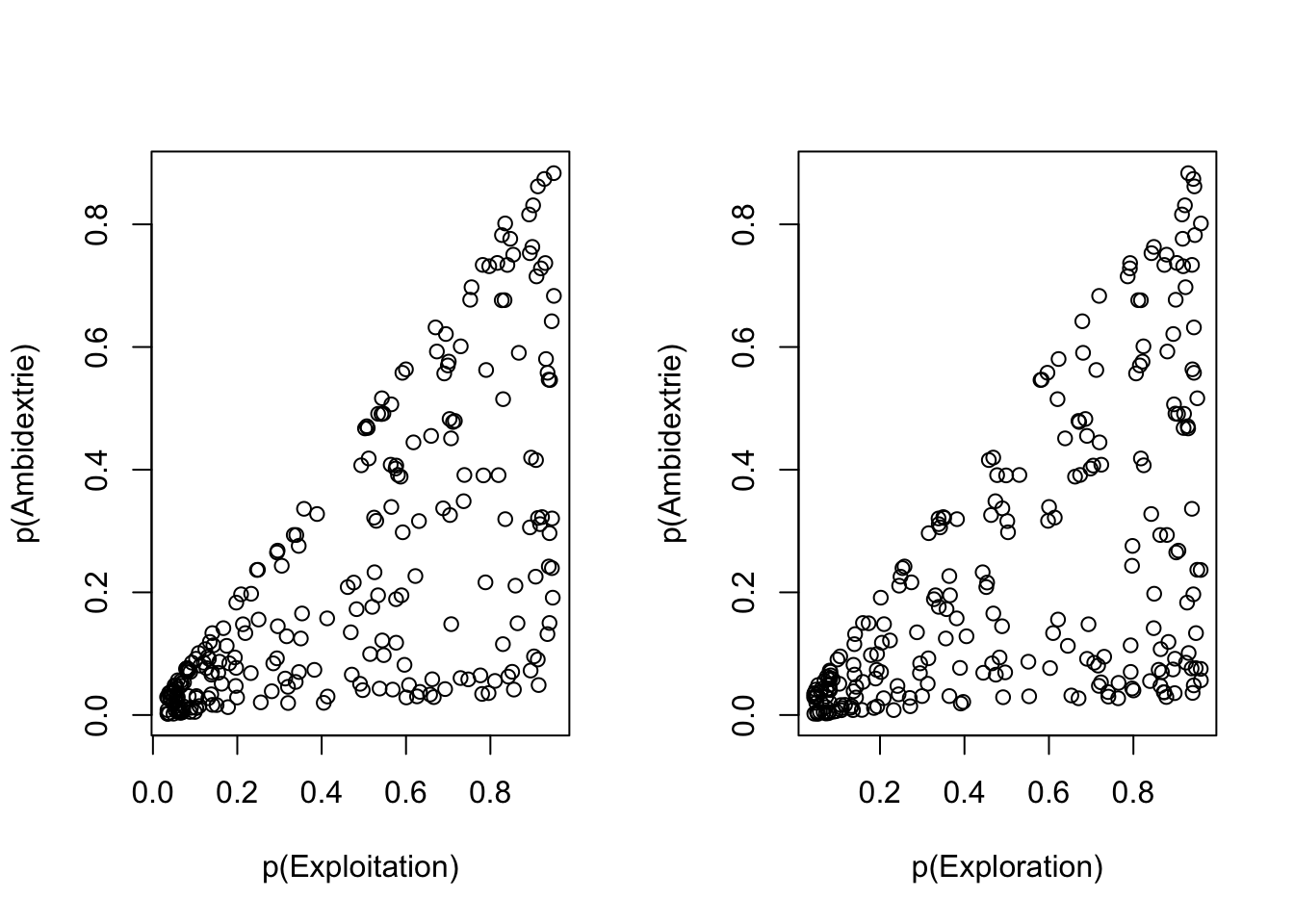
Sowohl für Exploitation als auch für Exploration zeigt sich das charakteristische Bild einer notwendigen Bedingung für Ambidextrie. Es gibt keine Fälle von Ambidextrie (P>0.5) ohne Exploitation (P<0.5) bzw. ohne Exploration (P<0.5).
Aufgrund der Annahme, dass Exploitation bei einer Wahrscheinlichkeit \(p(Exploitation)>0.5\) vorliegt und gleiches auf Exploration übertragbar ist, liegt komplementäre Ambidextrie für alle diejenigen Fälle vor, in denen \(p(Exploitation) & p(Exploration)>0.5\).
Diese Form der Operationalisierung kontrastiert also nicht die Symmetrie von Exploitation oder Exploration gegenüber der Dominanz einer der beiden strategischen Ausrichtungen, sondern die Wahrscheinlichkeit, dass Exploitation und Exploration vorliegen gegenüber der Wahrscheinlichkeit dass nur eine oder keine der beiden strategischen Ausrichtungen verfolgt wird.
par(mfrow=c(1,2))
plot(Ambidextrie, Ambidextrie_log, xlab=("Symmetrische Ambidextrie"), ylab="p(Ambidextrie)")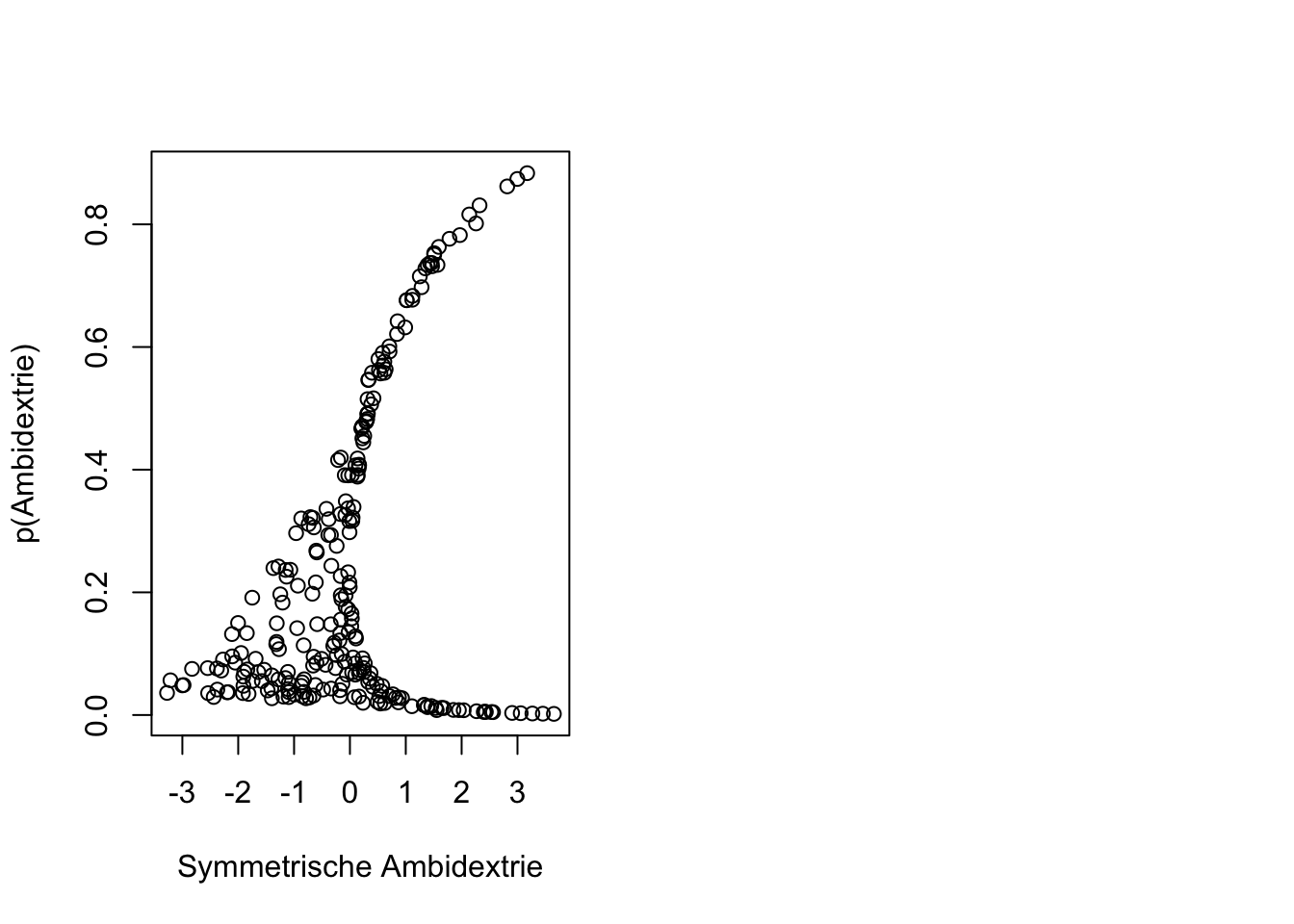
Wird diese Operationalisierung der Ambidextrie mit der Variante der Symmetrie verglichen, zeigt sich, dass eine hohe Wahrscheinlichkeit für Ambidextrie niemals ohne hohe Symmetrie existiert. Symmetrie ist eine notwendige Bedingung für die Wahrscheinlichkeit von Ambidextrie. Es zeigt sich aber auch, dass hohe Symmetrie vorliegen kann und die Wahrscheinlichkeit für Ambidextrie gering ist. Diese Situation wird durch die Datenpunkten rechts unten aufgezeigt. Sie repräsentieren die Form von symmetrischer Ambidextrie, bei welcher Exploitation und Exploration Zahlenwerte <0 annehmen.
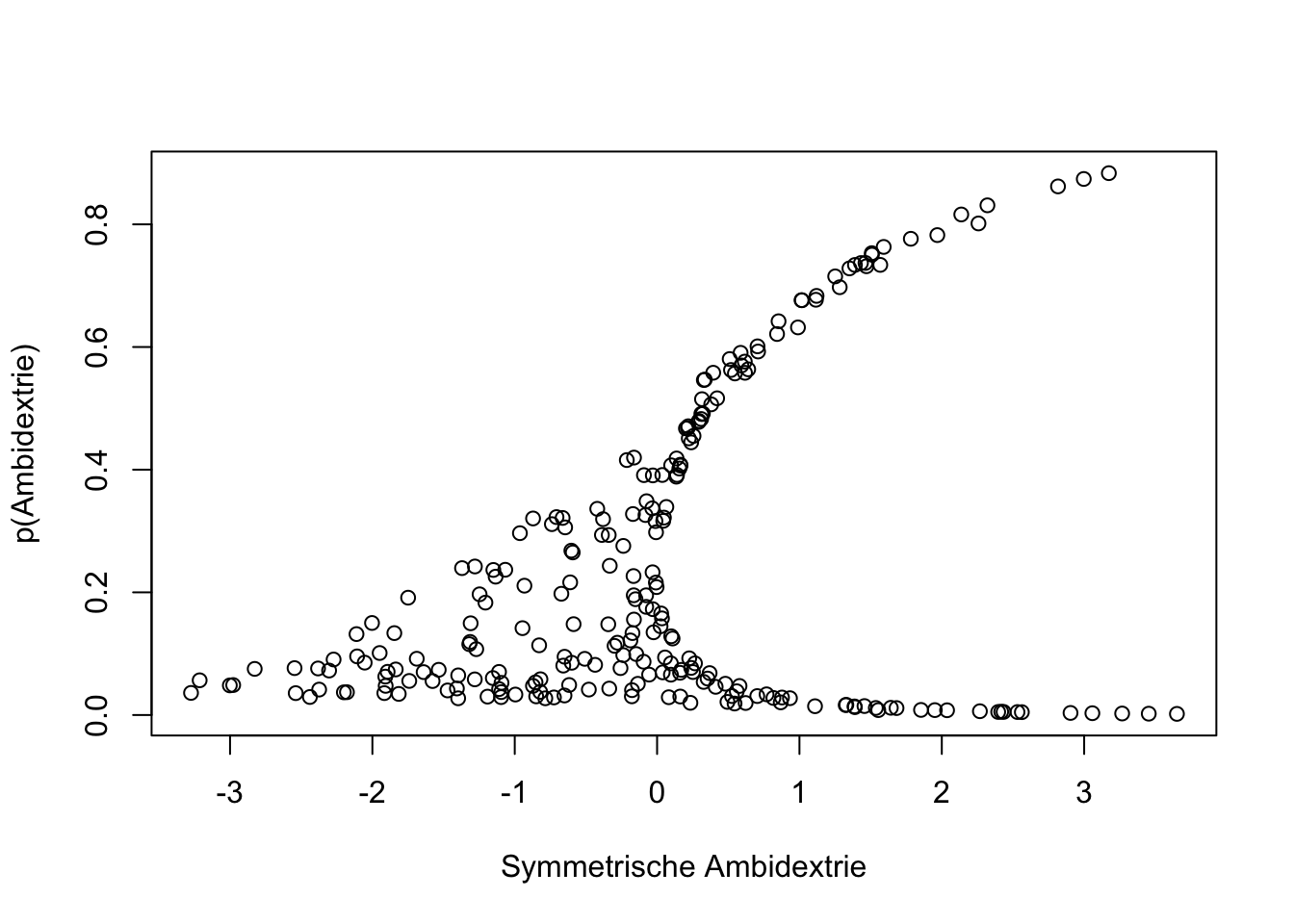
Konsequenter Weise unterscheiden sich auch die Koeffizienten aus in einer Regression mit diesen Werten auf Unternehmenserfolg.
##
## Call:
## lm(formula = Unternehmenserfolg ~ p_exploi + p_explor + Ambidextrie_log)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.15530 -0.32636 0.01314 0.31635 1.26363
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.00721 0.09153 32.85 <2e-16 ***
## p_exploi -6.24468 0.16396 -38.09 <2e-16 ***
## p_explor -6.03091 0.14837 -40.65 <2e-16 ***
## Ambidextrie_log 12.46671 0.26903 46.34 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4343 on 246 degrees of freedom
## Multiple R-squared: 0.8985, Adjusted R-squared: 0.8972
## F-statistic: 725.6 on 3 and 246 DF, p-value: < 2.2e-16Die folgende Tabelle vergleicht die beiden Modelle, nach denen Ambidextrie als Symmetrie oder als Komplementarität operationalisiert wurden. Beide Modelle weisen mit \(R^2>0.8\) eine hohe Anpassungsgüte auf. Das Modell mit symmetrischer Ambidextrie unterstützt die Annahme, dass eine Balance zwischen Exploitation und Exploration den Unternehmenserfolg fördert, auch wenn beide gering ausgeprägt sind. Dieser Befund könnte z.B. darauf hinweisen, dass in diesem Fall (geringe Exploitation und geringe Exploration) eine weitere exklusive oder subsituierende strategische Ausrichtung vorliegt. Eine Dominanz von Exploitation oder Exploration würde jedoch in jedem Fall mit geringerem Unternehmenserfolg assoziiert werden.
Das Modell mit der Operationalisierung von komplementärer Ambidextrie zeigt auf, dass eine hohe Wahrscheinlichkeit von Exploitation mit geringerem Unternehmenserfolg assoziiert ist, wenn sie mit einer unklaren Wahrscheinlichkeit für Exploration (50%) einhergeht. Umgekehrt ist auch Exploration negativ mit Unternehmenserfolg assoziiert, wenn die Wahrscheinlichkeit von Exploitation 50 Prozent beträgt.
Dem gegenüber wird der Unternehmenserfolg mit steigender Wahrscheinlichkeit von Exploitation und Exploration gefördert.
\[\begin{array}{|c|c|c|c|c|c|} \hline \ & Symmetrie & & Komplementarität & \\ \hline \ Term & beta & p & beta & p \\ \hline \text{Konstante} & \text{-0.01} & \text{.517} & \text{3.01} & \text{.000} \\ \text{Exploitation} & \text{0.04} & \text{.065} & \text{-6.24} & \text{.000} \\ \text{Exploration} & \text{-0.01} & \text{.739} & \text{-6.03} & \text{.000} \\ \text{Ambidextrie} & \text{1.00} & \text{.000} & \text{12.47} & \text{.000} \\ \hline \ R^2 & \text{0.937} & \text{} & \text{0.897} & \text{} \\ \hline \end{array}\]
Wenn die beiden Modelle als Interaktions-Plot dargestellt, zeigt sich ein deutlich unterschiedliches Bild. Das Modell mit symmetrischer Operationalisierung von Ambidextrie (links) bildet genau diesen Zusammenhang ab. Ein hoher Unternehmenserfolg wird prognostiziert, wenn Exploitation und Exploration beide gering bzw. wenn beide hoch ausgeprägt sind.
Das Modell mit komplementärer Operationalisierung (rechts) bildet hingegen den komplementären Zusammenhang von Exploitation und Exploration auf den Unternehmenserfolg ab. Damit der Unternehmenserfolg voll entfaltet wird, bedarf es einer hohen Wahrscheinlichkeit für Exploration (durchgezogene Linie) und eine hohe Wahrscheinlichkeit für Exploration.
Die prognostizierten Beträge des Unternehmenserfolges, wie sie in der folgenden Abbildung dargestellt sind, weisen eine hohe Übereinstimmung auf. Die Daten unterstützen beide Modelle und liefern unterschiedliche Befunde bei nahezu identischer Anpassungsgüte.
UE_1 = -0.01 + 0.04*Exploitation + (-0.01*Exploration) + 1.00*Exploitation*Exploration
UE_2 = 3.01 + (-6.24* p_exploi) + (-6.03*p_explor) + (12.47*Ambidextrie_log)
plot(Unternehmenserfolg, UE_1, col = "blue", xlim = range(-4, 4), ylim = range(-4, 4), xlab = "Wahrer Unternehmenserfolg", ylab = "Prognosen des Unternehmenserfolges", main = "Wahre Werte und Modellschätzungen")
points(Unternehmenserfolg, UE_2, col = "red")
legend("topleft", legend = c("Symmetrie", "Komplementarität"), col = c("blue", "red"), pch = c(16, 18), lty = 2)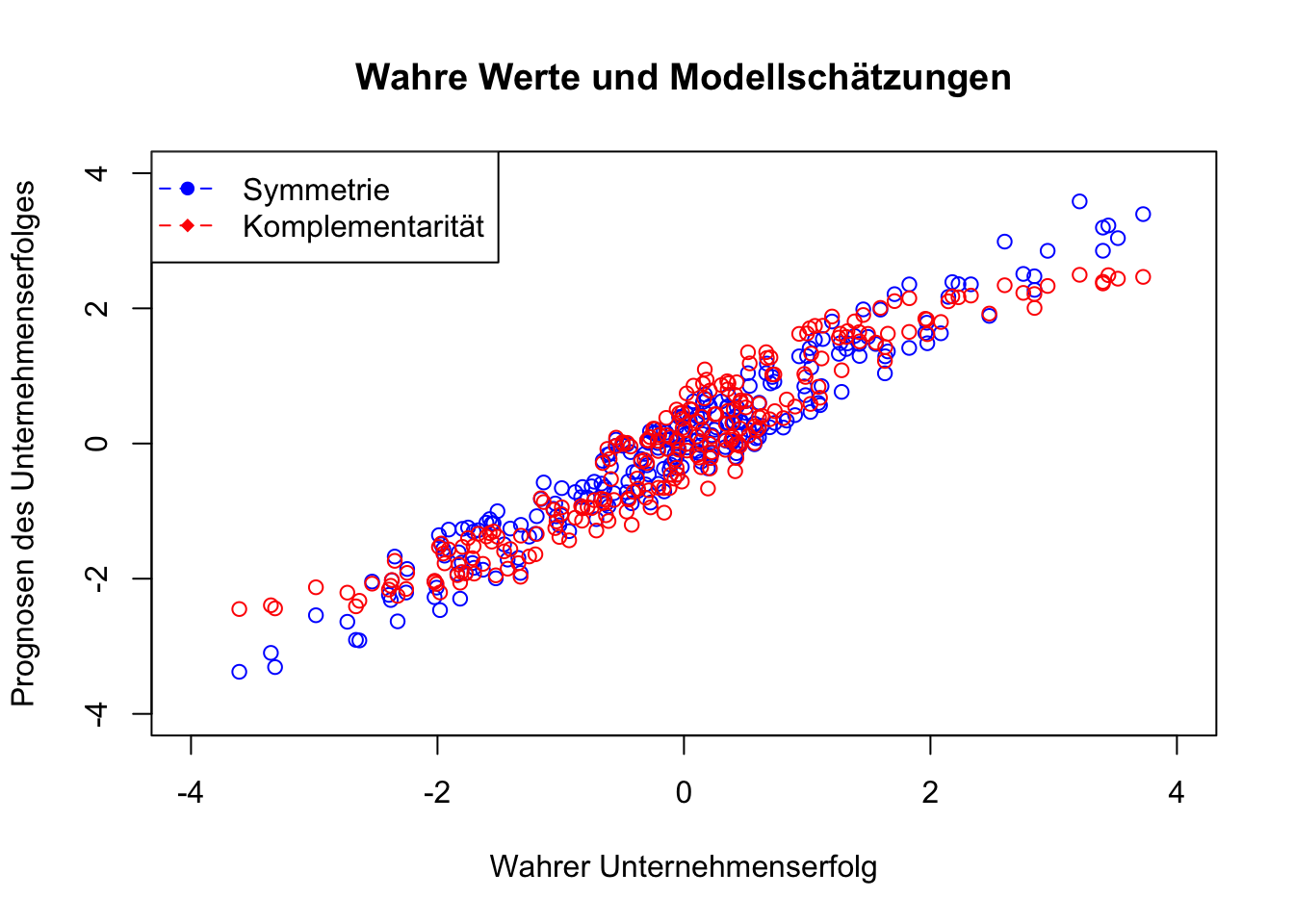
Ankerpunkte
Es wurde schon dargestellt, dass die logistische Funktion durch den Erwartungswert \(\alpha\) der logistischen Verteilungen und der Steilheit der logistischen Verteilung (\(\beta\)) bestimmt wird.
\(\alpha\) ergibt sich aus dem Median der Daten und \(\beta\) aus ihrer Varianz. Im Kontext der Kalibrierung werden dabei die Begriffe Ankerpunkt verwendet. \(\alpha\) bestimmt den Schwellenwert (“Crossover-point”), an welchem die Wahrscheinlichkeitsfunktion den Wert \(P=0.5\) aufweist. \(\beta\) bestimmt den die Beträge über (“full-membership”) und unter (“full non-membership”) dem Schwellenwert, die mit Wahrscheinlichkeiten gegen 0 bzw. 1 assoziiert sind.
Als theoretische Ankerpunkte bei einer 5-stufigen Skala werden die Skalenpunkte 1, 3 und 5 verwendet, welche den Raum zwischen den semantischen Kategorien “Stimme nicht zu”, “teils/ teils” und “Stimme zu” abbilden.
Als empirische Ankerpunkte eignen sich beispielsweise das 5%-, 50%- und 95%-Perzentil der Variable, um Grade der Nicht-Mitgliedschaft, den Schwellenwert und der vollständigen Mitgliedschaft zu definieren.
6.3.3 Rasch-Modell
Die probabilistische Theorie wird oft durch das Rasch-Modell oder ändere ähnliche Modelle dargestellt.Es wird hauptsächlich zur Analyse von Daten verwendet, die aus Antworten auf Tests oder Fragebögen stammen, insbesondere wenn diese Daten kategoriale Antwortmöglichkeiten (z.B. richtig/falsch, Zustimmung/Ablehnung) umfassen.
Ein zentrales Merkmal des Rasch-Modells ist die spezifische Objektivität. Das bedeutet, dass die Messungen von Personenfähigkeiten unabhängig von den speziellen Items im Test sind (und umgekehrt). Diese Eigenschaft ermöglicht es, dass die Fähigkeiten der Personen und die Schwierigkeiten der Items auf derselben Skala gemessen und direkt miteinander verglichen werden können.
Wenn das Rasch-Modell auf Umfragedaten, z.B. zu betrieblichen Struktureigenschaften, angewendet wird, hilft es dabei, die Messgenauigkeit von Items zu überprüfen, indem es die Wahrscheinlichkeit modelliert, dass eine Person eine bestimmte Antwort gibt, abhängig von ihrer Fähigkeit (oder ihrer Einstellung zu einem betrieblichen Thema) und der Schwierigkeit des Items. Dies kann besonders nützlich sein, um zu verstehen, wie gut verschiedene Items zwischen Befragten mit unterschiedlichen Perspektiven oder Kenntnissen differenzieren.
Das Modell unterstützt die Erstellung von Skalen, die unabhängig von der spezifischen Stichprobe der Befragten sind, was bedeutet, dass die Ergebnisse über verschiedene Gruppen hinweg vergleichbar sind. Es kann auch dazu beitragen, Items zu identifizieren, die möglicherweise nicht gut funktionieren oder verzerrt sind, was für die Verbesserung von Umfragen zu betrieblichen Struktureigenschaften entscheidend sein kann.
Damit ist das Rasch-Modell ist eine spezielle Form der Item Response Theory (IRT), das auf einer sehr spezifischen Annahme über die Beziehung zwischen der Fähigkeit einer Person und der Wahrscheinlichkeit einer bestimmten Antwort basiert,
Dabei ist das Rasch Modell als ein 1-Parameter-Modell in der IRT, weil es nur die Schwierigkeit des Items (Item-Schwierigkeit) als variablen Parameter berücksichtigt. Es wird angenommen, dass alle Items die gleiche Diskriminierungsfähigkeit haben.
Im Folgenden werden die Aussagen von 691 Menschen analysiert, die ihrer Beschäftigung in Coworking-Spaces nachgehen.
- Ich habe in meiner primären Arbeitsorganisation ein hohes Ansehen.
- Ich werde in der Lage sein, die meisten Ziele zu erreichen, die ich mir gesetzt habe.
- Ich bin mir sicher, dass ich schwierige Aufgaben meistern werde.
- Im Allgemeinen denke ich, dass ich alle Ziele erreichen kann, die mir wichtig sind.
- Ich werde viele Herausforderungen erfolgreich meistern können.
- Ich bin zuversichtlich, dass ich viele verschiedene Aufgaben bewältigen kann.
- Ich bin gut darin, Probleme kreativ zu lösen.
- Ich glaube, dass ich gut darin bin, neuartige Ideen zu generieren.
- Ich habe das Talent, die Ideen anderer weiterzuentwickeln.
- Ich bin mit meinem Gehalt zufrieden.
- Ich fühle mich finanziell abgesichert.
- Alle meine Talente und Fähigkeiten werden bei der Arbeit auch genutzt.
- Grundsätzlich kommt meine Arbeit meinem Ideal sehr nahe.
- Die Bedingungen bei meiner Arbeit sind ausgezeichnet.
- Bezüglich meiner zukünftigen Karriere bin ich optimistisch.
Offensichtlich hat das erste Item nichts mit den folgenden zu tun. Die Aussage bezieht sich hauptsächlich auf den Status einer Person innerhalb ihrer Arbeitsorganisation, da sie auf die Anerkennung und den Respekt abzielt, den die Person von anderen erhält. Narzissmus könnte zwar eine Rolle spielen, aber die Aussage selbst beschreibt eher eine objektive soziale Stellung als ein Persönlichkeitsmerkmal.
Zwischen den Bewertungen bestehen diverse hohe Korrelationen:
## K1 K2 K3 K4 K5 K6 K7 K8 K9 K10 K11 K12 K13 K14 K15
## K1 1.00 0.59 0.50 0.47 0.46 0.45 0.37 0.46 0.49 0.43 0.42 0.45 0.57 0.47 0.41
## K2 0.59 1.00 0.62 0.64 0.60 0.59 0.52 0.54 0.54 0.41 0.36 0.46 0.51 0.52 0.53
## K3 0.50 0.62 1.00 0.66 0.76 0.70 0.57 0.53 0.52 0.34 0.29 0.43 0.52 0.37 0.60
## K4 0.47 0.64 0.66 1.00 0.71 0.68 0.53 0.54 0.54 0.31 0.30 0.46 0.48 0.47 0.51
## K5 0.46 0.60 0.76 0.71 1.00 0.71 0.55 0.53 0.52 0.28 0.25 0.45 0.51 0.43 0.61
## K6 0.45 0.59 0.70 0.68 0.71 1.00 0.63 0.59 0.56 0.36 0.29 0.40 0.48 0.42 0.57
## K7 0.37 0.52 0.57 0.53 0.55 0.63 1.00 0.65 0.62 0.42 0.36 0.43 0.48 0.44 0.52
## K8 0.46 0.54 0.53 0.54 0.53 0.59 0.65 1.00 0.64 0.39 0.33 0.44 0.47 0.42 0.46
## K9 0.49 0.54 0.52 0.54 0.52 0.56 0.62 0.64 1.00 0.40 0.43 0.46 0.51 0.44 0.44
## K10 0.43 0.41 0.34 0.31 0.28 0.36 0.42 0.39 0.40 1.00 0.76 0.54 0.60 0.55 0.44
## K11 0.42 0.36 0.29 0.30 0.25 0.29 0.36 0.33 0.43 0.76 1.00 0.49 0.60 0.57 0.47
## K12 0.45 0.46 0.43 0.46 0.45 0.40 0.43 0.44 0.46 0.54 0.49 1.00 0.70 0.54 0.50
## K13 0.57 0.51 0.52 0.48 0.51 0.48 0.48 0.47 0.51 0.60 0.60 0.70 1.00 0.69 0.62
## K14 0.47 0.52 0.37 0.47 0.43 0.42 0.44 0.42 0.44 0.55 0.57 0.54 0.69 1.00 0.58
## K15 0.41 0.53 0.60 0.51 0.61 0.57 0.52 0.46 0.44 0.44 0.47 0.50 0.62 0.58 1.00Die Aussagen 12-14 beziehen sich auf Merkmale der Zufriedenheit mit der Arbeit. Diese drei Items werden hier in einem Rasch-Modell dargestellt.
Während das dichotome Rasch-Modell binäre Werte vorsieht, kann ein Partial-Credit-Modell die 5-stufigen Anwortskalen verarbeiten. Um das Rasch-Modell durchzuführen muss dafür die kleinste Antwortkategorie (“trifft garnicht zu”) dem Wert 0 zugeordnet werden. Weil im Datenformat bislang 1-5 vorgesehen war, wird jeweils 1 subtrahiert und im Anschluss werden die Daten in eine Matrix konvertiert.
Zuerst wird mit der Schätzung eines RSM (Rating Scale Model) begonnen und anschließend werden die entsprechenden Kategorien-Schnittpunktparameter mit der Funktion thresholds() berechnet (Patrick Mair, 2024). Aus dem Ergebnis ist erkennbar, dass die Intervalle zwischen den Skalenpunkten nicht den gleichen Abstand aufweisen.
##
## Design Matrix Block 1:
## Location Threshold 1 Threshold 2 Threshold 3 Threshold 4
## K12 1.64858 0.01608 0.19263 2.05390 4.33170
## K13 1.62446 -0.00804 0.16851 2.02978 4.30758
## K14 1.62446 -0.00804 0.16851 2.02978 4.30758Der Lageparameter ist im Wesentlichen die Item-Schwierigkeit, und die Schwellen sind die Punkte im ICC-Diagramm (Item Characteristic Curve), an denen sich die Kategorienkurven schneiden. Lageparameter und Threshold1 sowie 4 können z.B. als empirische Ankerpunkte für die Kalibrierung verwendet werden. Sollte die ursprüngliche Skalierung von 1 bis 5 verwendet werden, muss jeweils wieder +1 additiert werden.
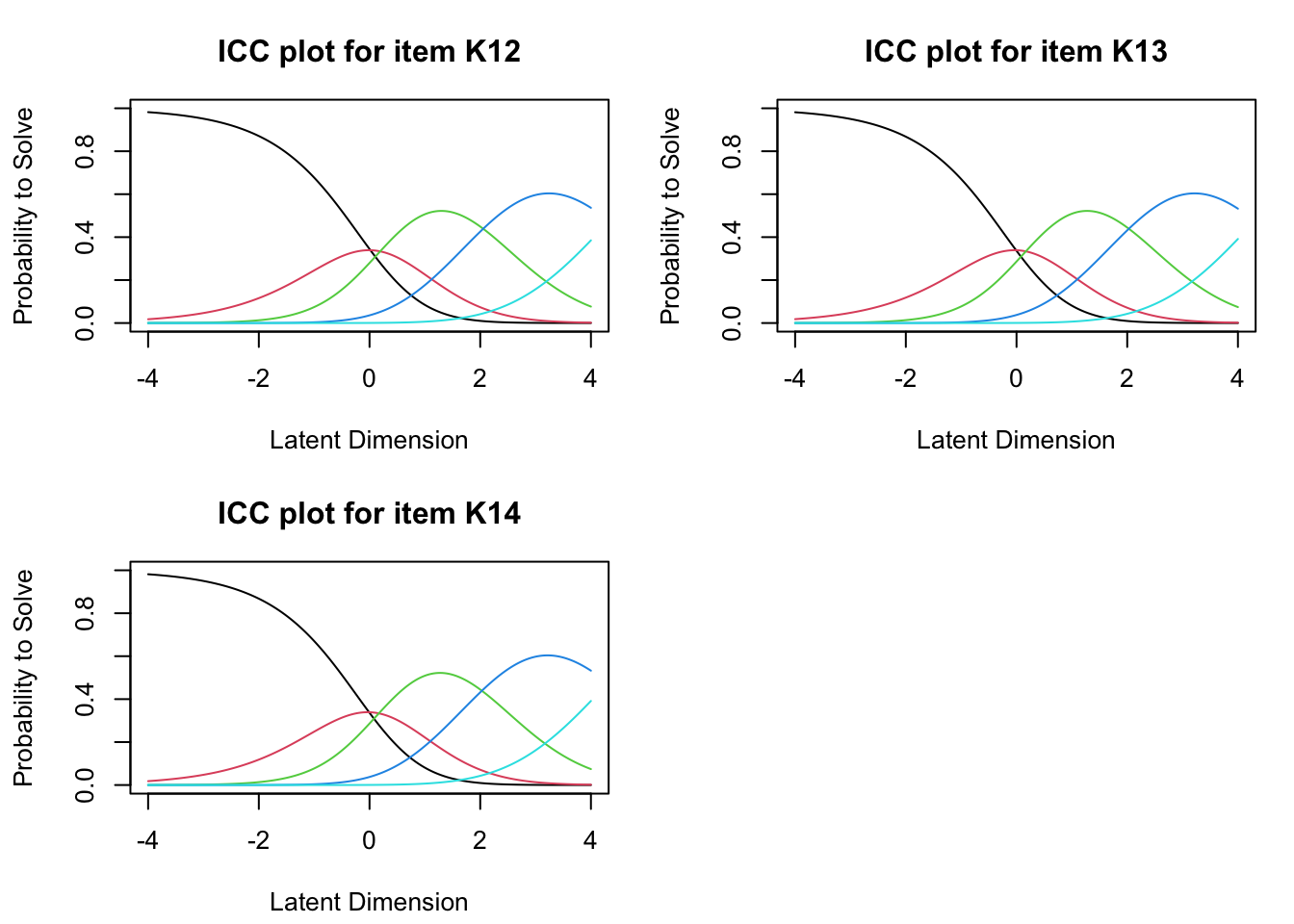
Das RSM (Rating Scale Model) hat die Annahme, dass die Schwellenabstände für alle Items gleich sind. Dies kann in manchen Datensätzen zu einer schlechten Modellanpassung führen. Diese strenge Forderung wird mit einem PCM (Partial Credit Model) gelockert. Die Ergebnisse werden in einer Personen-Item-Map dargestellt. Die Personen-Item-Map ist ein grafisches Werkzeug, dass die zugrundeliegende Aussage der Befragten und die Schwierigkeiten der Items auf einer gemeinsamen Skala visualisiert. Diese Darstellung hilft dabei, das Zusammenspiel zwischen Befragten und Items besser zu verstehen und zu analysieren.
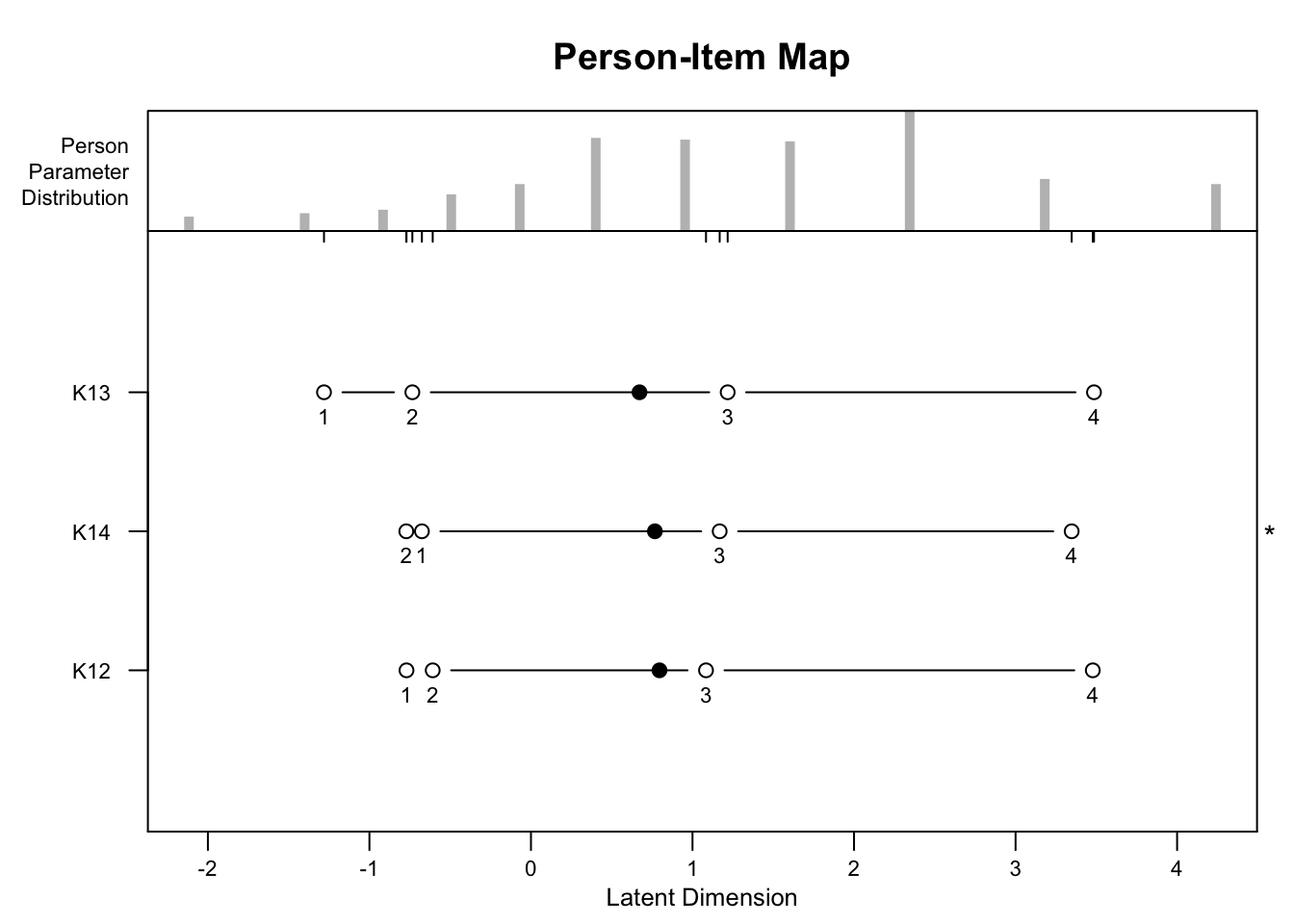Nach der Schätzung der Personenparameter werden hier die Item-Fit-Statistiken überprüft.
##
## Itemfit Statistics:
## Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t Discrim
## K12 234.168 308 0.999 0.758 0.754 -3.227 -3.236 0.532
## K13 157.803 308 1.000 0.511 0.503 -7.473 -7.478 0.739
## K14 232.374 308 1.000 0.752 0.775 -3.309 -2.924 0.516Die Chi-Quadrat-Statistik wird verwendet, um die Abweichung zwischen den beobachteten und den erwarteten Antwortmustern zu bewerten. Ein signifikanter Chi-Quadrat-Wert kann darauf hinweisen, dass das Item nicht gut zum Modell passt.
Die Outfit- und Infit-Mean-Squares (MSQ) weisen idealerweise einen Wert von 1 auf. Werte zwischen 0,5 und 1,5 gelten im Allgemeinen als akzeptabel, wobei Werte unter 1 auf ein zu wenig variierendes und Werte über 1 auf ein zu stark variierendes Antwortverhalten hinweisen.
Die Diskriminanz gibt an, wie sensitiv ein Item auf Unterschiede in den Aussagen der Befragten reagiert. Ein hohes Diskriminationsvermögen bedeutet, dass das Item gut zwischen Befragten mit verschiedenen Ausagen-Niveau differenziert, während ein niedriges Diskriminationsvermögen darauf hinweist, dass das Item dies weniger effektiv tut. Wie schon aus der Person-Item-Map ersichtlich wurde, weisst die Aussage K13 (“Grundsätzlich kommt meine Arbeit meinem Ideal sehr nahe.”) die höchste Diskriminanz zwischen hohen und geringen Bewertungen auf.
Der folgende Likelihood-Ratio-Test (LRT), der das RSM mit dem PCM vergleicht, zeigt an, dass das PCM keine bessere Anpassung bietet. Der LRT-Teststatistik weist einen \(p=0.84\) auf.
lr <- 2 * (res.pcm$loglik - res.rsm$loglik)
df <- res.pcm$npar - res.rsm$npar
pvalue <- 1 - pchisq(lr, df)
cat("LR statistic: ", lr, " df =", df, " p =", pvalue, "\n")## LR statistic: 2.737832 df = 6 p = 0.8409586Gleiches wird im Folgenden für die Items K2 bis K6 dargestellt. Hierbei handelt es sich um positive Affirmationen als Form von Resilienz. Der signifikante Chi^2-Test weist darauf hin, dass die Aussage “Ich werde in der Lage sein, die meisten Ziele zu erreichen, die ich mir gesetzt habe.” nicht gut mit zum Rasch-Modell passt.
##
## Design Matrix Block 1:
## Location Threshold 1 Threshold 2 Threshold 3 Threshold 4
## K2 2.67150 0.40854 1.51935 2.94313 5.81499
## K3 2.27028 0.00731 1.11813 2.54190 5.41377
## K4 2.27881 0.01584 1.12666 2.55043 5.42230
## K5 1.99790 -0.26507 0.84575 2.26952 5.14139
## K6 2.09633 -0.16663 0.94419 2.36796 5.23982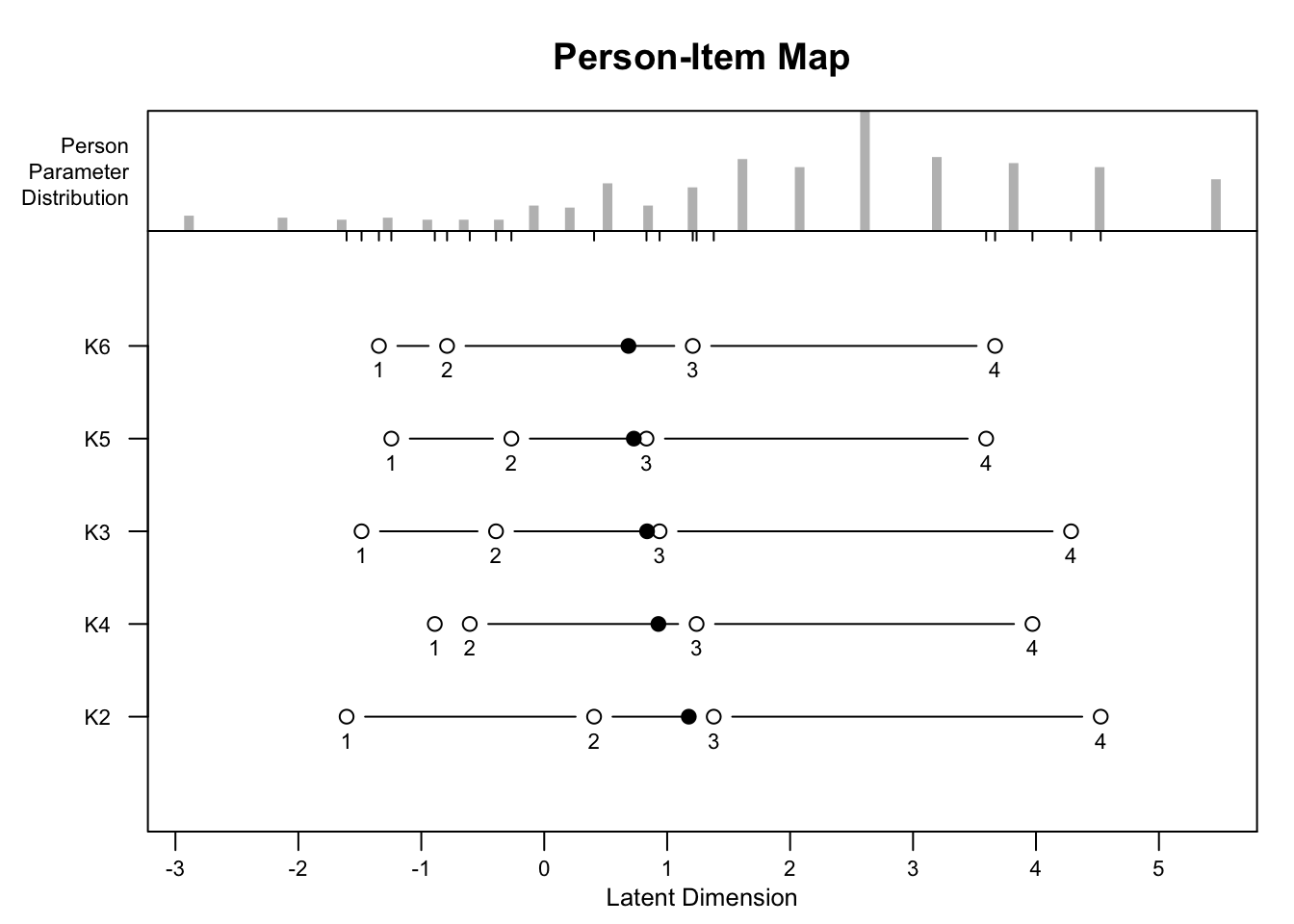
##
## Itemfit Statistics:
## Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t Discrim
## K2 325.701 291 0.079 1.115 1.069 1.334 0.808 0.561
## K3 213.415 291 1.000 0.731 0.725 -3.333 -3.333 0.744
## K4 232.543 291 0.995 0.796 0.788 -2.481 -2.525 0.712
## K5 178.664 291 1.000 0.612 0.654 -5.027 -4.339 0.795
## K6 244.197 291 0.979 0.836 0.797 -1.967 -2.463 0.713## LR statistic: 15.09769 df = 12 p = 0.23613766.4 Konditionale Abhängigkeit
Konditionale Abhängigkeit bezieht sich darauf, wie die Wahrscheinlichkeit eines Ereignisses von einem anderen Ereignis abhängt, gegeben, dass ein weiteres, drittes Ereignis bereits eingetreten ist. Dies bedeutet, dass die Beziehung zwischen zwei Ereignissen durch die Information über das dritte Ereignis bedingt wird.
Auch wenn der Zusammenhang zwischen zwei Variablen in Regressionsmodellen vielfach als Zusammenhang zwischen unabhängiger und abhängiger Variable bezeichnet wird, oder der Einfluss der unabhängigen Variable auf die abhängige Variable suggeriert, dass es sich hier um kausale Abhängigkeiten handeln könnte, ist dem nicht so. Zwei Variablen weisen einen Zusammenhang auf, wenn der Koerrelationskoeffizient dieses Variablenpaares nicht Null beträgt bzw. wenn in einer Regression ein signifikant von Null abweichender \(\beta\)-Koeffizienten resultiert.
Zusammenhang kann und wird, wie es Pearson, Lee & Bramley-Moore (1899) bezeichnet, konstruiert: “To those who persist on looking upon all correlation as cause and effect, the fact that correlation can be produced between two quite uncorrelated characters A and B by taking an artificial mixture of the two closely allied races, must come as rather a shock.” (Pearson et al., 1899, S. 278)
Wenn ein Zusammenhang zwischen zwei Variablen besteht, dann korrelieren diese Variablen. Weicht der Korrelationskoeffizient nicht signifikant von Null ab, besteht kein Zusammenhang.
Dem gegenüber sind zwei Variablen abhängig voneinander, wenn ihre gemeinsame Wahrscheinlichkeitsfunktion für alle x und y nicht dem Produkt ihrer marginalen Wahrscheinlichkeitsfunktionen entspricht. Das heißt, formal ausgedrückt:
\[ P_{X,Y}(x,y) \neq P_X(x) \cdot P_Y(y) \] Dies bedeutet, dass die Wahrscheinlichkeit, dass beide Variablen bestimmte Werte annehmen, nicht einfach durch das Produkt der einzelnen Wahrscheinlichkeiten dieser Werte bestimmt werden kann.
Dies bedeutet, dass die gemeinsame Wahrscheinlichkeitsfunktion der beiden Variablen gleich dem Produkt der einzelnen Wahrscheinlichkeitsfunktionen der Variablen ist, was auf Unabhängigkeit hinweist.
\[ P_{X,Y}(x,y) = P_X(x) \cdot P_Y(y)\] 1. Wenn X und Y nicht unabhängig sind, dann sind sie abhängig. (Wenn zum Beispiel die Variable Y eine Funktion von X ist, dann sind X und Y immer abhängig.)
Wenn X und Y unabhängig sind, dann sind die ebenfalls unkorreliert.
Wenn X und Y unkorreliert sind, dann sind sie oft ** nicht unabhängig**.
Nur wenn X und Y normalverteilt sind, dann bedeutet keine Korrelation auch Unabhängigkeit.
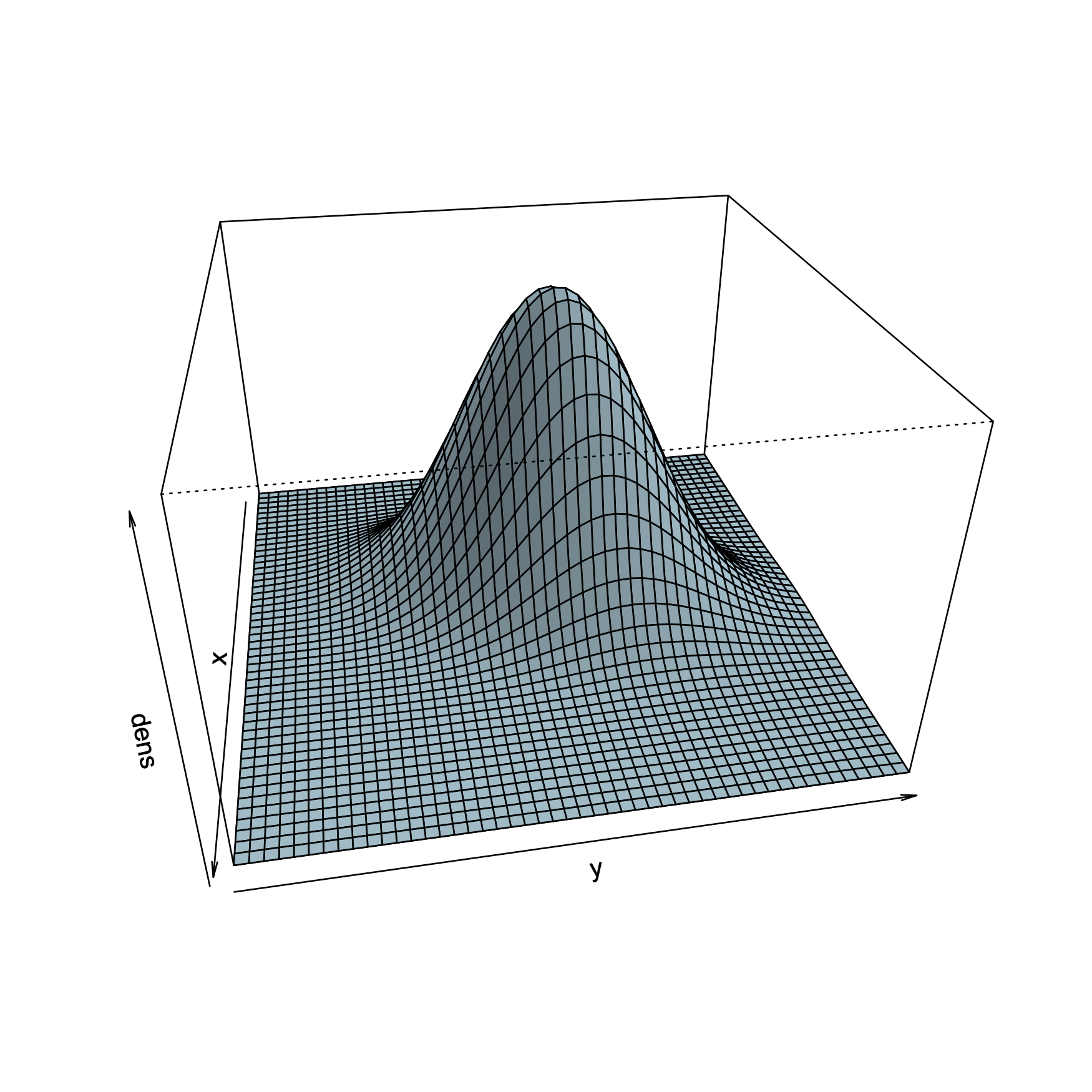
Der vierte Punkt bezieht sich auf das Konzept der multivariaten Normalverteilung. Wenn man die Häufigkeitsverteilungen zweier Variablen auf die Achsen eines Koordinatensystems überträgt, ergibt sich eine dreidimensionale Glockenkurve. Dies ist jedoch in den meisten Fällen nicht gegeben.
Im Zusammenhang mit multivariaten Regressionen ist immer wieder deutlich geworden, dass sich die Koeffizienten der unabhängigen Variablen in der Regressionsgleichung unterscheiden können, wenn eine weitere Variable berücksichtigt oder unberücksichtigt bleibt. Im Beispiel zur Mediation wurde aufgezeigt, dass Trainings die Kompetenzen von Mitarbeitern gefördert haben und dass diese Kompetenzen zu höheren Leistungen führen können. Wurden Trainings und Kompetenzen in der multivariaten Regression unter den spezifischen Bedingungen der Mediationsanalyse Baron & Kenny (1986) analysiert, hat der insignifikante Koeffizient einer unabhängigen Variablen in multivariaten Regressionen auf eine Abfolge von Ereignissen verwiesen.
In der Moderator-Analyse nach Baron & Kenny (1986) wurde die Entscheidung, ob eine Variable als Moderator für den Zusammenhang zwischen einer unabhängigen Variablen und einer abhängigen Variablen anzusehen ist, ausschließlich an der Signifikanz des Koeffizienten für den Produkt-Term entschieden, während Inkonsistenzen in den geschätzten Koeffizienten für die unabhängigen Variablen keine Beachtung fanden.
In beiden Fällen werden Entscheidungen über die kausalen Beziehungen von mindestens drei Variablen im Modell getroffen. Weil der Mediator den Zusammenhang zwischen unabhängiger Variablen und abhängiger Variablen vermittelt, ist er – kausal betrachtet – ein Ergebnis der unabhängigen Variablen und eine Ursache hinsichtlich der abhängigen Variablen.
In seiner idealen Form ist ein Moderator hingegen weder Ergebnis noch Ursache der unabhängigen Variablen und der abhängigen Variablen. Vielmehr ist der Moderator die Ursache für den Zusammenhang der beiden Variablen. Damit zeigt ein Moderator einen ganz spezifischen Kontext auf, in dem ein Zusammenhang zwischen unabhängiger Variablen und abhängiger Variablen besteht oder auch nicht.
6.4.1 Marginale (konditionale) Effekte
Wenn Moderatoren identifiziert sind, besteht auch Interesse in der Art der Moderation, der Frage bei welcher Ausprägung des Moderators, welcher Einfluss der unabhängigen Variable auf die abhängige Variable zu erwarten ist. Im Folgenden handelt es sich um das Regressionsmodell, dass bereits im Abschnitt “Substitution” dargestellt wurde.
##
## Call:
## lm(formula = Kompetenz ~ Training + Erfahrung + Training_Erfahrung)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.85963 -0.20336 0.03828 0.18249 0.81553
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.26598 0.52833 -13.75 <2e-16 ***
## Training 2.50499 0.11305 22.16 <2e-16 ***
## Erfahrung 2.71668 0.12424 21.87 <2e-16 ***
## Training_Erfahrung -0.56502 0.02693 -20.98 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3314 on 246 degrees of freedom
## Multiple R-squared: 0.6688, Adjusted R-squared: 0.6648
## F-statistic: 165.6 on 3 and 246 DF, p-value: < 2.2e-16Das Regressionsmodell schätzt die Koeffizienten auf Grundlage der unabhängigen Variable (\(x\)), des Moderators (\(z\)) und des Produktterms (\(xz\)). Die typischen Interaktionsplots von Dawson (2014) eignen sich nicht, weil sie nicht den moderierten Effekt von X auf Y darstellen, sondern die Prognose der abhängigen Variable \(\hat{y}\) auf Grundlage der unabhängigen Variable (\(x\)), des Moderators (\(z\)) und ihres Produktterms (\(x \cdot z\)). \[ \hat{y}=\beta_0 + \beta_1x+\beta_2z+\beta_3xz\] \(\beta_1\) zeigt hier den Beitrag von \(x\) zu \(\hat{y}\) auf, wenn \(z\) einen Zahlenwert von Null aufweist. Weil in diesem Beispiel keine Zentrierung vorgenommen wurde und der Zahlenbereich von \(1.01 ≤ z ≤ 4.99\) reicht, ist die Annahme \(z=0\) eine rein theoretisch-mathematische Information.
Umgekehrt zeigt \(\beta_2\) den Beitrag von \(z\) zu \(\hat{y}\) auf, wenn \(x\) einen Zahlenwert von Null aufweist. Die Variable Trainings weist einen Zahlenbereich von \(1.37 ≤ x ≤ 4.99\). Auch der Koeffizient \(\beta_2\) indiziert also einen Beitrag zu \(\hat{y}\), der sich auf einen Wert außerhalb des empirisch Gemessenen bezieht.
Darüber hinaus weist der Koeffizient \(\beta_3\) auf den Beitrag von \(x \cdot z\) bzgl. \(\hat{y}\) hin.
Um den Beitrag von \(x\) auf \(\hat{y}\) im empirischen Bereich von \(z\) zu bestimmen, wird der marginaler Effekt durch die folgende Gleichung bestimmt:
\[ ME_{Y|X;Z}= \beta_1+\beta_3z \]
Vorausgesetzt \(\beta_3 \neq 0\), weist die Gleichung für unterschiedliche Ausprägung von \(Z\) variierende Beiträge von \(X\) zu \(Y\) auf.
Bezogen auf das obrige Beispiel wird der marginale Effekt von Trainings auf die Kompetenz, abhängig von der Vorerfahrung bestimmt als:
\[ ME_{Kompetenz|Training; Erfahrung}= 2.50 + (-0.57 \cdot Erfahrung) \] wobei: \(1.01 ≤ Erfahrung ≤ 4.99\)
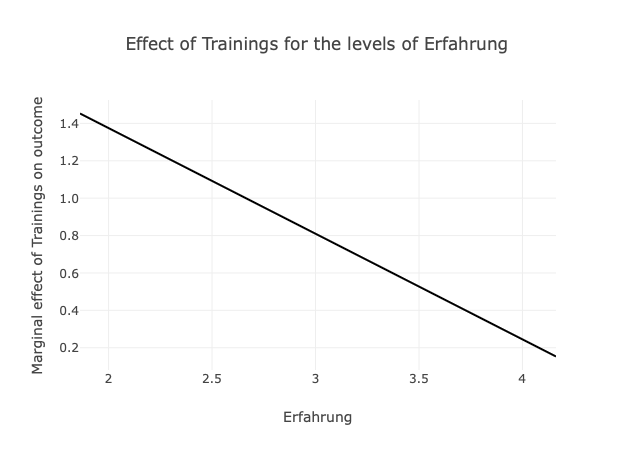
Der positive Beitrag von Trainings auf Kompetenz nimmt demnach mit steigender Vorerfahrung ab und erreicht bei den hohen Werten in Erfahrung (\(\overline z + SD_z\)) einen Beitrag zu \(\hat y\) von nahezu Null (0.15).
Anmerkung: Handelt es sich bei \(Z\) um eine zentrierte Variable, bezeichnet der resultierende Effekt für \(Z=0\) den durchschnittlichen marginalen Effekt (\(AME\)). Anderenfalls sind die Randeffekte zu berechnen für \(Z_{Low}=\overline{z}-SD(z)\) und \(Z_{High}=\overline{z}+SD(z)\). Der durchschnittliche marginale Effekt beträgt dann \(AME_{Y|X;Z}= \beta_1+\beta_3\overline{z}\).
6.4.2 Endogenität
Die experimentelle Annahme, dass die Variationen in der abhängigen Variablen einzig durch die Variation einer unabhängigen Variablen verursacht sind, ist in den meisten Datensammlungen weder intendiert noch haltbar.
Die Manipulation spezifischer Variablen (z.B. der Ausprägung einer spezifischen Strategie oder die Höhe der Forschungsintensität) ist in der angewandten Unternehmungsforschung in der Regel nicht durchsetzbar und es existieren unterschiedlichste Ansichten, ob einige Auswertungsverfahren überhaupt sinnvoll angewandt werden können.
“Perhaps the most critical challenge arises from the fact that … research … is based on data where the researcher merely observes the variables in a statistical sample. In an experiment one would manipulate x. When variables are merely observed, we do not know what the origins of their variances are. This also implies that we do not know whether or not they covary with one another” (Ketokivi & McIntosh, 2017, S. 2).
Endogenität beschreibt ein Konzept von Verzerrung und Inkonsistenz durch die Korrelation der unabhängigen, bzw. besser erklärenden Variable und dem Fehlerterm eines Regressionsmodells. Dies sei an einem Datensatz verdeutlicht, mit dem Antonakis (2011) das Problem der Endogenität aufzeigt.
# Ansicht der Daten von Antonakis (2011)
data <- read.csv2("data/2slsdata.csv", header=TRUE)
head(data)## q m n x y
## 1 0.6797270 0.6104631 -0.6721706 -0.0032122 1.3907760
## 2 -0.1129162 -0.3484794 2.1662550 2.9380260 -2.5697680
## 3 -0.0012075 -1.3779280 -1.0415740 -3.6526230 1.2777890
## 4 0.1700897 1.6838430 -0.3630079 0.2283438 1.1615960
## 5 0.7070127 1.3649760 -1.6379100 0.9267017 -0.8638926
## 6 -0.6984928 0.2998515 1.1231170 -1.5377530 -1.1251140Stark vereinfacht dargestellt hat er in diesem Datensatz die wahre Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variable y auf einen Wert von -0.30 festgelegt. Zudem besteht in diesem Modell ein weiterer Einfluss durch eine Variablen q, die auf beide Variablen x und y wirkt.
plot(data$x,data$y, xlim=c(-5,5),ylim=c(-5,5),
xlab="X-Variable",ylab="Y-Variable",
panel.first=grid(), col="blue")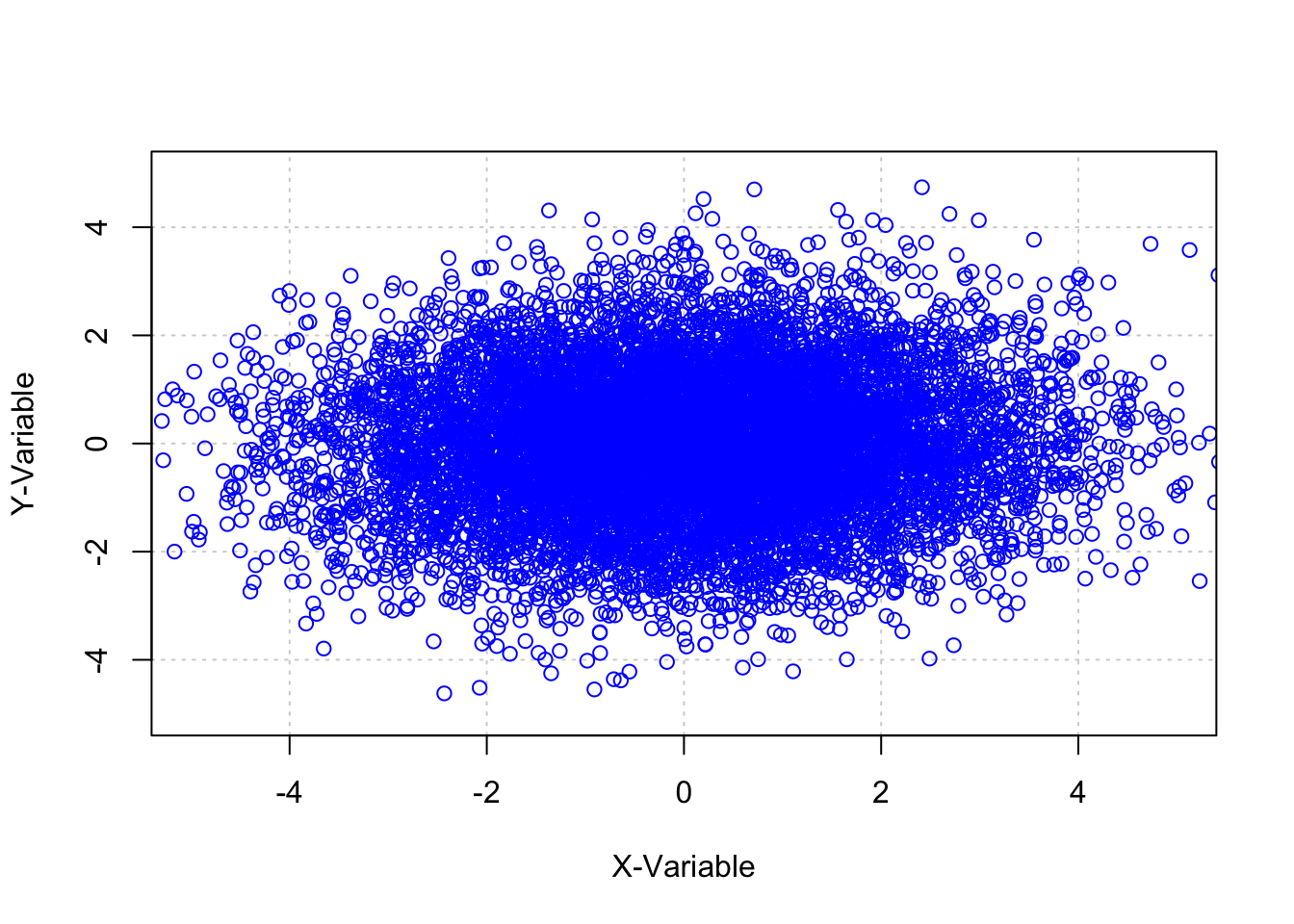
Bestimmen wir anhand dieser Daten in einer einfachen Regression den Einfluss von x auf y, bekommen wir für den Steigungskoeffizienten ein Ergebnis von b=0.033, welches zudem mit einem p-Wert von kleiner 0.001 höchst signifikant ausfällt.
##
## Call:
## lm(formula = y ~ x, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5318 -0.8614 0.0077 0.8715 4.6860
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.009860 0.012956 -0.761 0.447
## x 0.032703 0.007473 4.376 1.22e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.296 on 9998 degrees of freedom
## Multiple R-squared: 0.001912, Adjusted R-squared: 0.001812
## F-statistic: 19.15 on 1 and 9998 DF, p-value: 1.219e-05Im Fall einer Hypothese, die davon ausgeht, dass eine Zunahme in x zu einer Steigerung in y führt, würden wir diese Hypothese zu Lasten der Nullhypothese (dass kein Zusammenhang besteht) annehmen. Wir würden also einen Beleg für eine Aussage schaffen, obwohl diese Aussage falsch ist.
Bestimmen wir die Parameter für die Multiple Regression von x und q auf y, erzielen wir für \(\beta_1\) (dem Steigungskoeffizienten von x) einen Wert von -0.30 und für \(\beta_2\) (dem Steigungskoeffizienten von q) einen Wert von 1.00. Beide Werte sind höchst signifikant mit einem Wert von p<0.001 und die Hypothese, dass die Zunahme in x zu einer Steigerung in y führt, würde richtig zurückgewiesen werden.
# Multiple lineare Regression: y wird erklärt durch x und q
model2 <- lm(y~x+q,data)
summary (model2)##
## Call:
## lm(formula = y ~ x + q, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8656 -0.6954 -0.0033 0.6841 3.4236
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.004879 0.010040 -0.486 0.627
## x -0.303346 0.007107 -42.680 <2e-16 ***
## q 1.003060 0.012299 81.554 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.004 on 9997 degrees of freedom
## Multiple R-squared: 0.4007, Adjusted R-squared: 0.4005
## F-statistic: 3342 on 2 and 9997 DF, p-value: < 2.2e-16In diesem Beispiel nicht auf Grund fehlender Signifikanz, sondern auf Grund des falschen Vorzeichens. In der Praxis ist es daher von hoher Bedeutung, solche möglichen Einflussgrößen durch Einschluss in das Regressionsmodell zu verringern. Damit ist z.B. der Einschluss geeigneter Kontrollvariablen gemeint, für welche keine Hypothesen formuliert werden, für die aber idealerweise Zusammenhänge aus der Literatur bekannt sind.
“If the relation between x and y is due, in part, to other reasons, then x is endogenous, and the coefficient of x cannot be interpreted, not even as a simple correlation (i.e., the magnitude of the effect could be wrong as could be the sign)” (Antonakis, Bendahan, Jacquart & Lalive, 2010, S. 1088).
In quasi allen nicht-experimentellen Studiendesigns ist es nahezu ungewiss, dass ein Zusammenhang zwischen zwei Variablen besteht, der nicht mindestens durch eine dritte Variable verursacht oder umgekehrt werden könnte.
Immer wenn Forscher den Einfluss einer unabhängigen Variablen x auf eine abhängige Variable y untersuchen, stellt sich also auch die Frage, ob die Analysen durch zusätzliche Variablen (sogenannte Kovariate oder Störfaktoren) angepasst werden sollten (Pearl, 2009b).
Ich möchte behaupten, dass wir oft, wenn wir versuchen Zustände oder Prozesse zu beobachten oder messen, Variablen monokausal zueinander in Bezug setzten, deren Zusammenhang tatsächlich durch weitere Dinge verursacht wird.
Trotzdem sprechen wir oft von Ursache und Wirkung und vergessen dabei, dass die Idee der Kausalität ein Modell unserer Vorstellung ist, um Realität zu verstehen, weil die Idee von der Kausalität für uns brauchbar und überzeugend ist. Ob sie wahr ist, können wir nicht wissen.
“The most popular statistical solution to the endogeneity problem is two-stage least squares (2SLS) regression (Model g), which involves applying a set of instrumental variables to the troublesome regressors before conducting the regression of theoretical interest (…). If the conditions for instrumental variables are satisfied, this approach will allow for consistent estimation of the parameters of interest, despite endogeneity due to omitted variables or measurement error” (Ketokivi & McIntosh, 2017, S. 12).
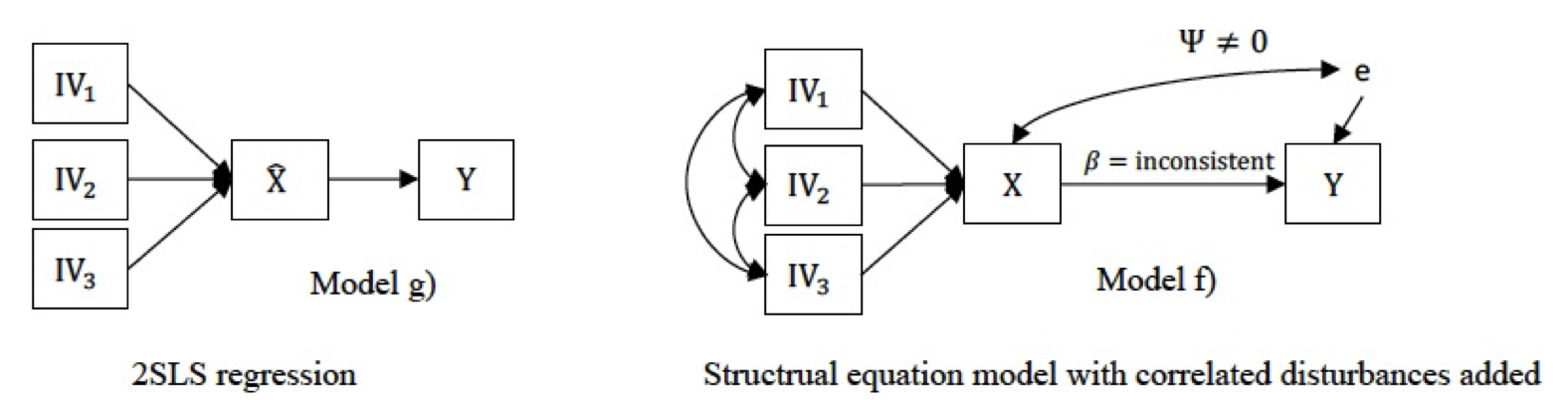
OLS ist ein effizienter Schätzer und es ist zu Prüfen, ob die Koeffizienten durch Endogenität verzerrt sind und zur falschen Interpretation der Ergebnisse führen. 2SLS sind robuster gegenüber Endogenitätsverzerrungen, jedoch weniger effizient als OLS.
Der Test auf schwache Instrumente (Weak-instruments-Test) prüft die Nullhypothese, dass alle Instrumente schwach sind. Mit einem geringen p-Wert ≤0.05 lehnen die Daten die Nullhypothese ab und unterstützen die Alternativhypothese, dass die Instrumente geeignet sind.
Der Wu-Hausman-Test kann verwendet werden, um die Konsistenz der OLS- und der 2SLS-Schätzung zu testen und ist dann ein Test auf Endogenität. Der Test überprüft, ob die Differenz zwischen den Schätzern signifikant ist, was darauf hinweist, ob die endogene Variable im Modell tatsächlich problematisch ist und daher ein Modell mit Instrumentalvariablen erforderlich ist. Ein geringer Wert in der Teststatistik, der mit einem hohen p-Wert einher geht, zeigt auf, dass die OLS- und 2SLS-Schätzer konsistent sind. Ein geringer p-Wert (z.B. <0.05) deutet darauf hin, dass die OLS-Schätzung verzerrt ist und eine 2SLS-Schätzung geeigneter ist.
Als Exogenitäts-Test prüft der Sargan-Test die Nullhypothese, dass die Instrumente exogen sind, das heißt, dass sie nicht mit dem Fehlerterm der geschätzten Gleichung korreliert sind. Ein hoher p-Wert (typischerweise > 0.05) unterstützt die Nullhypothese und deutet darauf hin, dass die Instrumente gültig sind. Ein niedriger p-Wert (typischerweise < 0.05) hingegen weist darauf hin, dass mindestens eines der Instrumente mit dem Fehlerterm korreliert ist und somit ungültig ist.
##
## Call:
## ivreg(formula = y ~ x | m + n, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.309826 -0.931823 0.008608 0.934721 5.435996
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.006456 0.014085 -0.458 0.647
## x -0.285930 0.014016 -20.401 <2e-16 ***
##
## Diagnostic tests:
## df1 df2 statistic p-value
## Weak instruments 2 9997 2529.000 <2e-16 ***
## Wu-Hausman 1 9997 1012.973 <2e-16 ***
## Sargan 1 NA 0.003 0.955
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.408 on 9998 degrees of freedom
## Multiple R-Squared: -0.1796, Adjusted R-squared: -0.1797
## Wald test: 416.2 on 1 and 9998 DF, p-value: < 2.2e-166.4.3 Prognosegüte (Holdout-Sample)
Neben dem OLS-Algorithmus gibt es auch andere Schätzer und Ansätze. Während viele Praktiker darauf versessen sind, austauschbare, teilweise willkürliche oder gar widersprüchliche Hypothesen mittels signifikanter Parameter zu beweisen, werden die Modellgüte, Fehlerterme (Residuen) oder Kennwerte der Prognosegüte sehr oft übersehen. Das ist sicher auch dadurch bedingt, dass einige Methoden die Datengrundlage reduzieren und die meist sowieso schon moderate Datenquantität (z.B. durch fehlende Werte) nicht weiter belastet werden kann. Der OLS-Algorithmus basiert auf der Methode, die Parameter des Regessionsmodells so zu schätzen, dass die Residuen, also die Abweichung der prognostizierten Werte der abhängigen Variablen von den tatsächlichen Werten, die der Schätzung zugrunde liegen, minimiert wird. Die Grundlage der Schätzung wird demnach zur Schätzung der Grundlage verwandt.
Eine geeignete Heuristik, diese Zirkulation zu durchbrechen, ist die zufällige Auswahl eines sogenannten Holdout-Sample. Häufig werden dabei 30% der Fälle ausgewählt - in kleinen Datensätzen auch mal nur 10% - und zur späteren Verwendung separiert.
Wie in der IV-Regression vorgesehen, werden zuerst die x anhand der Instrumentalvariablen m und n geschätzt.
ivmodel <- lm(x~m+n, train_data)
intercept = coef(summary(ivmodel))[1]
coefficients_m <- coef(summary(ivmodel))[2]
coefficients_n <- coef(summary(ivmodel))[3]
train_data$x_iv = intercept + (coefficients_m * train_data$m + coefficients_n * train_data$n)Anschließend werden die Parameter des Regressionsmodells im Training Sample aufgrund der geschätzten \(\hat{x}\) bestimmt. Den geschätzten Parameter benennen wir als “IV” für instrumental variables.
ivmodel <- lm(y~x_iv, train_data)
intercept_iv = coef(summary(ivmodel))[1]
coefficients_x_iv <- coef(summary(ivmodel))[2]Zudem werden die Parameter des Regressionsmodells im Training Sample aufgrund der tatsächlichen \({x}\) und unter Berücksichtigung von {q} bestimmt. Den geschätzten Parameter benennen wir als “purged” um zu bezeichnen, dass er bereinigt ist (Antonakis et al. (2010); Antonakis et al. (2014)).
purgemodel <- lm(y~x+q, train_data)
intercept_purge = coef(summary(purgemodel))[1]
coefficients_x_purge <- coef(summary(purgemodel))[2]
coefficients_q_purge <- coef(summary(purgemodel))[3]Zuletzt werden die Parameter des Regressionsmodells im Training Sample aufgrund der tatsächlichen \({x}\) und ohne Berücksichtigung von {q}, {n} und {m} bestimmt. Den geschätzten Parameter benennen wir als “unpurged” um zu bezeichnen, dass er verzerrt bze. verunreinigt ist (vgl. Antonakis).
unpurgemodel <- lm(y~x, train_data)
intercept_unpurge = coef(summary(unpurgemodel))[1]
coefficients_x_unpurge <- coef(summary(unpurgemodel))[2]Im Holdout-Sample berechnen wir nun für alle drei Modelle die geschätzen \(\hat y\) und quadrierten Abweichungen der Schätzungen von den wahren Werten:
\[ e_{iv}= (y-\hat y_{iv})^2\] \[ e_{purge}= (y-\hat y_{purge})^2\] \[ e_{unpurge}= (y-\hat y_{unpurge})^2\]
Um die quadrierten Fehler im Häufigkeitsdiagramm vergleichend darzustellen, werden sie umkodiert und aggregiert.
