Kapitel 5 Konzepte
In meinem zweiten Vortrag hatte ich die Kovarianzen und Korrelationen als Zusammenhangsmaße und die Regressionsanalyse als Prognosemodell vorgestellt, wobei wir zwischen deterministischen und stochastischen Modellen unterschieden hatten.
5.1 Multiple Regression
Der Einsatz von Regressionsverfahren wird jedoch praktisch in den seltensten Fällen mit nur einer unabhängigen Variablen durchgeführt. Wird die im Modell zu bestimmende Regressionsgleichung um eine zweite unabhängige Variable z erweitert, ergibt sich die Funktion:
\[ y_i=\beta_0 + \beta_1 x_i + \beta_2 z_i + e_i \]
Aus einem solchen multiplen Regressionsmodell (mit zwei unabhängigen Variablen: x und z) können “Aussagen über den gleichzeitigen Einfluss mehrerer unabhängiger Variablen auf eine zu erklärende Variable” getroffen werden (Dolic, 2010, S. 220).
Das Modell erfordert jedoch spezifische Voraussetzungen, deren Verletzung zu einer verzerrten oder inkonsistenten Schätzung der Regressionsparameter führen kann (ebenda) und worauf wir später noch zu sprechen kommen werden.
Der Parameter b (der Steigungskoeffizient in der einfachen Regression) wird in der multiplen Regression durch mehrere (in diesem Beispiel durch zwei) unabhängige Variablen bestimmt. Die resultierenden Parameter \(\beta\) werden daher in der Regel mit fortlaufenden Nummern versehen.
In diesem Fall bestimmt \(\beta_1\) , um welchen Wert sich die abhängige Variable verändert, wenn x um den Wert von 1 zunimmt und \(\beta_2\) bestimmt, um welchen Wert sich die abhängige Variable verändert, wenn z um einen Wert von 1 zunimmt. Außerdem wird in der Gleichung für das multiple Regressionsmodell der Parameter a (der Schnittpunkt der Geraden mit der y-Achse) als \(\beta_0\) bezeichnet. An seiner Interpretation ändert sich nichts.
Das Residuum \(\varepsilon_i\) in der einfachen Regressionsgleichung wird durch den Fehlerterm \(e_i\) ersetzt. Diese Unterscheidung soll darauf hinweisen, dass der Fehlerterm (disturbance term) in dieser Funktion inhaltlich alle unberücksichtigten Quellen für Variationen in Y sowie jeder anderen Fehlerquelle (z.B. Messfehler) einschließt. In diesem Sinn unterscheidet sich das Residuum \(\varepsilon_i\) vom Fehlerterm \(e_i\) (Antonakis, Bendahan, Jacquart & Lalive, 2014, S. 14).
Sowohl die Bestimmung mittels Statistikprogrammen als auch die Interpretation der Koeffizienten hinsichtlich ihrer Signifikanz unterscheidet sich nicht von der einfachen Regression. Im Gegensatz zur einfachen Regression werden die Determinationskoeffizienten aber höher ausfallen, wenn Sie zwei geeignete unabhängige Variablen verwenden.
5.1.1 Exkurs: Experiment
Die Annahme, dass die Variationen in der abhängigen Variablen durch die Variation der unabhängigen Variablen verursacht sind, wird traditionell in Experimenten untersucht. Dabei werden die unabhängigen Variablen manipuliert (d.h. es werden unterschiedlichen Ausprägungen festgelegt) und die daraus resultierenden Variationen der abhängigen Variablen gemessen.
Da eine solche Manipulation der unabhängigen Variablen (z.B. der Ausprägung einer spezifischen Strategie oder die Höhe der Forschungsintensität) in der angewandten Unternehmungsforschung in der Regel nicht durchsetzbar ist, existieren unterschiedlichste Meinungen darüber, ob diese analytischen Auswertungsverfahren überhaupt sinnvoll angewandt werden können.
5.1.2 Exkurs: Endogenität
“Perhaps the most critical challenge arises from the fact that … research … is based on data where the researcher merely observes the variables in a statistical sample. In an experiment one would manipulate x. When variables are merely observed, we do not know what the origins of their variances are. This also implies that we do not know whether or not they covary with one another” (Ketokivi & McIntosh, 2017, S. 2).
Verschiedene Untersuchungen haben gezeigt, dass die Ergebnisse aus nicht-experimentell erhobenen Daten deutlichen Fehlern in Form verzerrter Parameterschätzungen unterliegen können. Dies sei an einem Datensatz von John Antonakis verdeutlicht, mit dem er das Problem der Endogenität erläutert (Antonakis, 2011).
# Ansicht der Daten von Antonakis (2011)
data <- read.csv2("data/2slsdata.csv", header=TRUE)
head(data)## q m n x y
## 1 0.6797270 0.6104631 -0.6721706 -0.0032122 1.3907760
## 2 -0.1129162 -0.3484794 2.1662550 2.9380260 -2.5697680
## 3 -0.0012075 -1.3779280 -1.0415740 -3.6526230 1.2777890
## 4 0.1700897 1.6838430 -0.3630079 0.2283438 1.1615960
## 5 0.7070127 1.3649760 -1.6379100 0.9267017 -0.8638926
## 6 -0.6984928 0.2998515 1.1231170 -1.5377530 -1.1251140Stark vereinfacht dargestellt hat er in diesem Datensatz die wahre Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variable y auf einen Wert von -0.30 festgelegt. Zudem besteht in diesem Modell ein weiterer Einfluss durch eine Variablen q, die auf beide Variablen x und y wirkt.
plot(data$x,data$y, xlim=c(-5,5),ylim=c(-5,5),
xlab="X-Variable",ylab="Y-Variable",
panel.first=grid(), col="blue")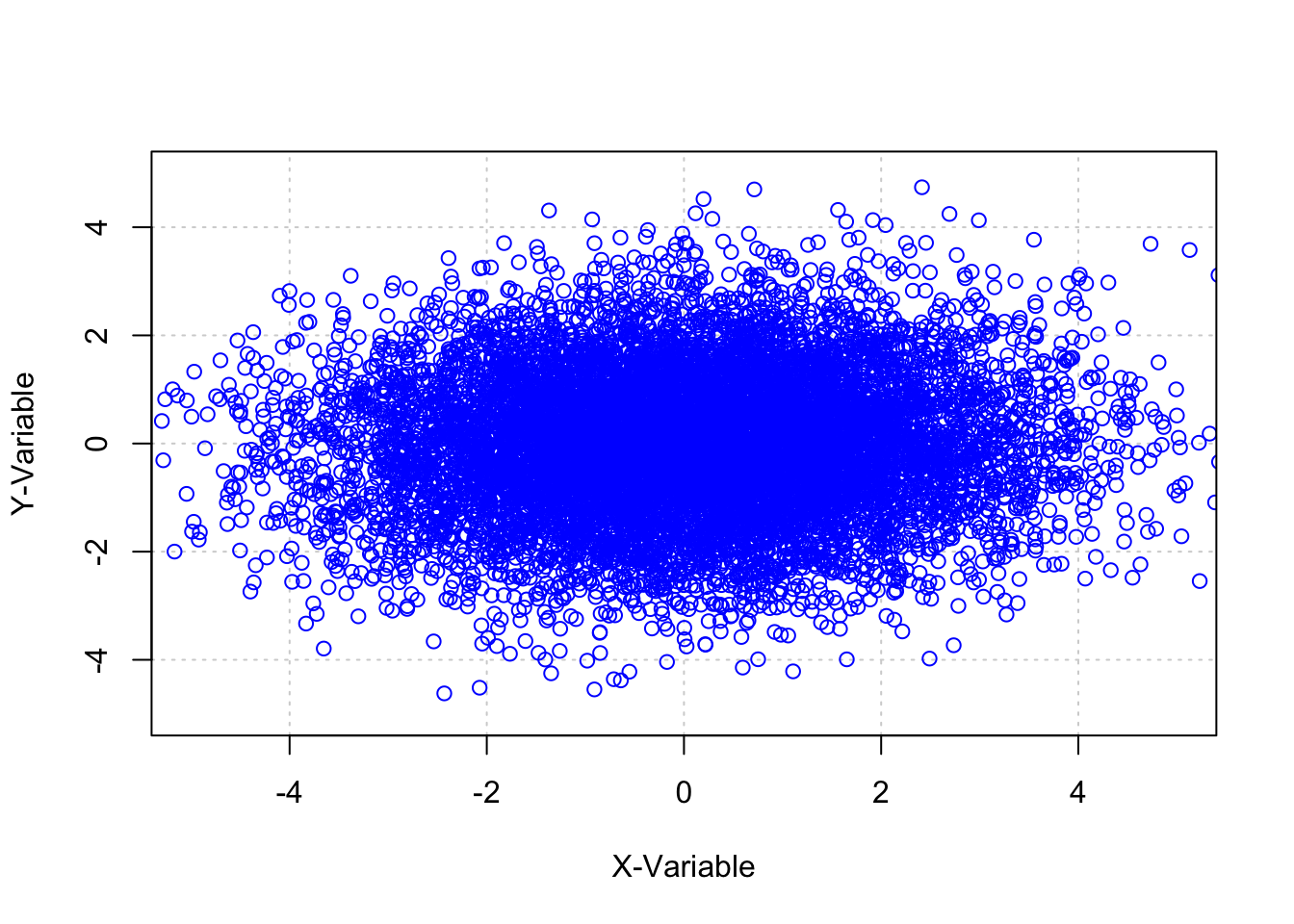
Bestimmen wir anhand dieser Daten in einer einfachen Regression den Einfluss von x auf y, bekommen wir für den Steigungskoeffizienten ein Ergebnis von b=0.033, welches zudem mit einem p-Wert von kleiner 0.001 höchst signifikant ausfällt.
# Einfache lineare Regression: y wird erklärt durch x
model1 <- lm(y~x,data)
summary (model1)##
## Call:
## lm(formula = y ~ x, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.5318 -0.8614 0.0077 0.8715 4.6860
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.009860 0.012956 -0.761 0.447
## x 0.032703 0.007473 4.376 1.22e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.296 on 9998 degrees of freedom
## Multiple R-squared: 0.001912, Adjusted R-squared: 0.001812
## F-statistic: 19.15 on 1 and 9998 DF, p-value: 1.219e-05Im Fall einer Hypothese, die davon ausgeht, dass eine Zunahme in x zu einer Steigerung in y führt, würden wir diese Hypothese zu Lasten der Nullhypothese (dass kein Zusammenhang besteht) annehmen. Wir würden also einen Beleg für eine Aussage schaffen, obwohl diese Aussage falsch ist.
Bestimmen wir die Parameter für die Multiple Regression von x und q auf y, erzielen wir für \(\beta_1\) (dem Steigungskoeffizienten von x) einen Wert von -0.30 und für \(\beta_2\) (dem Steigungskoeffizienten von q) einen Wert von 1.00. Beide Werte sind höchst signifikant mit einem Wert von p<0.001 und die Hypothese, dass die Zunahme in x zu einer Steigerung in y führt, würde richtig zurückgewiesen werden.
# Multiple lineare Regression: y wird erklärt durch x und q
model2 <- lm(y~x+q,data)
summary (model2)##
## Call:
## lm(formula = y ~ x + q, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8656 -0.6954 -0.0033 0.6841 3.4236
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.004879 0.010040 -0.486 0.627
## x -0.303346 0.007107 -42.680 <2e-16 ***
## q 1.003060 0.012299 81.554 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.004 on 9997 degrees of freedom
## Multiple R-squared: 0.4007, Adjusted R-squared: 0.4005
## F-statistic: 3342 on 2 and 9997 DF, p-value: < 2.2e-16In diesem Beispiel nicht auf Grund fehlender Signifikanz, sondern auf Grund des falschen Vorzeichens. In der Praxis ist es daher von hoher Bedeutung, solche möglichen Einflussgrößen durch Einschluss in das Regressionsmodell zu verringern. Damit ist z.B. der Einschluss geeigneter Kontrollvariablen gemeint, für welche keine Hypothesen formuliert werden, für die aber idealerweise Zusammenhänge aus der Literatur bekannt sind.
“If the relation between x and y is due, in part, to other reasons, then x is endogenous, and the coefficient of x cannot be interpreted, not even as a simple correlation (i.e., the magnitude of the effect could be wrong as could be the sign)” (Antonakis, Bendahan, Jacquart & Lalive, 2010, S. 1088).
In quasi allen nicht-experimentellen Studiendesigns ist es nahezu ungewiss, dass ein Zusammenhang zwischen zwei Variablen besteht, der nicht mindestens durch eine dritte Variable verursacht oder umgekehrt werden könnte.
Immer wenn Forscher den Einfluss einer unabhängigen Variablen x auf eine abhängige Variable y untersuchen, stellt sich also auch die Frage, ob die Analysen durch zusätzliche Variablen (sogenannte Kovariate oder Störfaktoren) angepasst werden sollten (Pearl, 2009a).
Ich möchte behaupten, dass wir oft, wenn wir versuchen Zustände oder Prozesse zu beobachten oder messen, Variablen monokausal zueinander in Bezug setzten, deren Zusammenhang tatsächlich durch weitere Dinge verursacht wird.
Trotzdem sprechen wir oft von Ursache und Wirkung und vergessen dabei, dass die Idee der Kausalität ein Modell unserer Vorstellung ist, um Realität zu verstehen, weil die Idee von der Kausalität für uns brauchbar und überzeugend ist. Ob sie wahr ist, können wir nicht wissen.
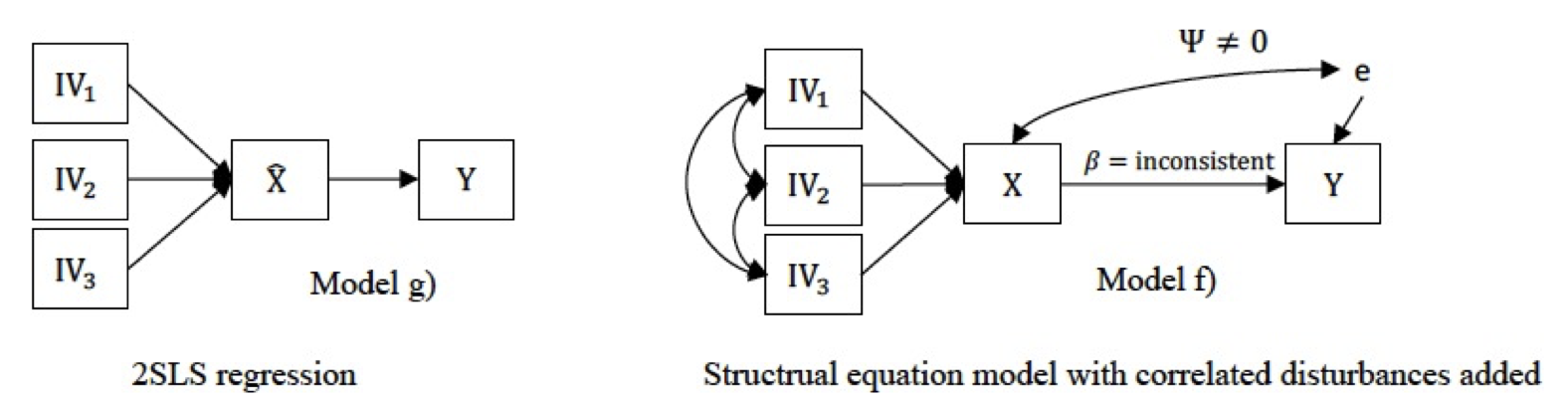
“The most popular statistical solution to the endogeneity problem is two-stage least squares (2SLS) regression (Model g), which involves applying a set of instrumental variables to the troublesome regressors before conducting the regression of theoretical interest (…). If the conditions for instrumental variables are satisfied, this approach will allow for consistent estimation of the parameters of interest, despite endogeneity due to omitted variables or measurement error” (Ketokivi & McIntosh, 2017, S. 12).
5.2 Kausalzusammenhänge
Eine verbreitete Definition für Kausalzusammenhänge fordert die Erfüllung von drei Bedingungen, damit Forscher eine Ursache und einen Effekt als Kausalzusammenhang darstellen können. Dies sind zeitliche Abfolge, Zusammenhang und Unverfälschtheit (Kenny, 2004).
5.2.1 Zeitliche Abfolge (time precedence)
Primär bezieht sich die zeitliche Abfolge von Ursache und Konsequenz auf eine Problemstellung, die zum großen Teil durch das Forschungsdesign (z.B. in Längsschnittstudien) bestimmt wird (Spector, 2019). In Längsschnittstudien werden die Ursachen als unabhängige Variablen zu einem Zeitpunkt \(t_0\) erhoben und die Konsequenz als abhängige Variable zu einem oder mehreren zeitlich verzögerten Zeitpunkten \(t_1\), \(t_2\), … , \(t_i\).
Entscheidend für die Dauer der zeitlichen Verzögerung ist die Erwartung, wann Konsequenzen aus den Ursachen zu erwarten sind. Dem Gegenüber weisen Querschnittstudien nur einen Erhebungszeitpunkt auf, zu dem sowohl die unabhängigen als auch die abhängigen Variablen erhoben werden (Spector, 2019).
Trotz dieser Einschränkung können Daten aus Querschnittstudien zum Nachweis von Ursache-Wirkungsbeziehungen nützlich sein. Eine zeitliche Abfolge wird beispielsweise in jeder retrospektiven Befragung durch theoretische Annahmen und die Formulierung der Items berücksichtigt.
So weist bei der Befragung von Kooperationsbeziehungen die Formulierung: ‘Welche Vorgaben hat der Kooperationspartner vor Kooperationsbeginn festgelegt’, gegenüber der Formulierung ‘Welche Modifikationen der Vorgaben wurden während der Kooperation nachträglich fixiert?’, auf einen vorgelagerten Zeitpunkt des Kooperationsprozesses hin.
Unter Berücksichtigung der Weiterentwicklung von Analysemethoden ist derzeit eine Liberalisierung der Forderung von Längsschnittstudien vorzufinden. So argumentiert (z.B. Spector, 2019), dass die Fähigkeit, Kausalität in Längsschnittdesigns zu reflektieren lange Zeit überbewertet wurde und dass es in den meisten Fällen, in denen es verwendet wird nur begrenzte Vorteile gegenüber dem Querschnittdesign aufweist [125].
5.2.2 Zusammenhang (relationship)
Wir haben bereits die Kovarianz, bivariate Korrelation und Regression als Maße für den assoziativen Zusammenhang zwischen Variablen (Kenny, 2004, S. 17) kennen gelernt. Diese Maße weisen auf bedeutsame Zusammenhänge hin, wenn sie Signifikanz aufweisen, d.h. wenn die Nullhypothese, dass der Zusammenhang einen wahren Wert von Null aufweist, zugunsten der Annahme, dass der Zusammenhang ungleich Null ist, zurückgewiesen wird. Für den Nachweis kausaler Abhängigkeiten sind signifikante Zusammenhangsmaße somit “eine notwendige, aber keine hinreichenden Voraussetzungen” (Bortz, 1993, S. 217).
Zudem haben wir bereits angesprochen, dass die Zusammenhangsmaße aus nicht-experimentell erhobenen Daten auch einer verzerrten Parameterschätzungen unterliegen können, womit wir bei Kenny’s dritter Bedingung angelangt sind (Kenny, 2004):
5.2.3 Unverfälschtheit (nonspuriousness): Exkurs Konditionale Unabhängigkeit
Wie bereits aufgezeigt, kann die Beziehung zwischen zwei Variablen x und y durch eine dritte Variable beeinflusst sein. Philip Dawid (1979) hat eine Notation vorgeschlagen, durch welche dargestellt werden soll, ob zwei Variablen voneinander unabhängig, bedingungslos unabhängig oder unabhängig, bedingt durch eine Drittvariable sind.
Konditionale Unabhängigkeit bezieht sich also auf den Fall, dass zwei Variablen X und Y, bedingt durch eine dritte Variable Z, voneinander unabhängig sind (Dawid, 1979). Ein Variablenpaar X, Y kann ebenso voneinander abhängig sein, bedingt durch eine dritte Variable Z.
Für ein Variablen-Triple (X, Y, Z) werden drei Formen unterschieden, welche die Grundlage dafür bilden, kausale Zusammenhänge möglicherweise aufzudecken. Die erste Form wird als ‘fork’ bezeichnet und gleicht einer Gabelung. Die Variablen X und Y, die voneinander nicht unabhängig (also abhängig) sind, werden in dieser Form bedingt durch die dritte Variable Z unabhängig.
Dies ähnelt dem dargestellten Beispiel von Antonakis (2011), bei dem der negative Zusammenhang zwischen X und Y verdeckt wurde, wenn die gemeinsame Ursache Q im Regressionsmodell unberücksichtigt blieb.
Die zweite Form bezeichnet eine Kette bzw. ‘chain’, bei welcher die Variable X auf die Variable Z wirkt und Z wiederum auf eine Variable Y wirkt. Auch in diesem Fall sind X und Y unabhängig, bedingt durch Z.
Die dritte Form wird als Kollision bzw. ‘collider’ bezeichnet. Bei dieser speziellen Form sind die Variablen X und Y primär unabhängig. Beide wirken auf eine dritte Variable Z. Dadurch bedingt sind X und Y nicht unabhängig, also abhängig bedingt durch Z.
Empirisch können ‘collider’ von ‘forks’ und ‘chains’ unterschieden werden . Aus solchen Annahmen entwickelte (Pearl, 2009b) ein Kriterium für die Entscheidung, ob eine Auswahl von Variablen X von einer Auswahl von Variablen Y, unter der Bedingung des Vorhandenseins dritter Variablen Z, als unabhängig anzusehen sind.
Dieses Kriterium geht also der Frage nach, ob X und Y als unabhängig anzusehen sind, wenn beide Variablen X und Y über eine dritte Variablen Z verbunden sind. Die Idee assoziiert Unabhängigkeit mit der Trennung des direkten Verbindungsweges bzw. Abhängigkeit mit direkter Verbundenheit (Pearl, 2009b, S. 335).
Ein Pfad zwischen den Variablen X und Y wird aus dieser Perspektive blockiert bzw. getrennt durch die Anwesenheit einer Variable Z.
Ein Pfad von X auf Y ist getrennt durch Z wenn und nur wenn der Pfad \(X\to Y\) eine Verkettung (chain) \((X \to Z \to Y)\) oder eine Gabelung (fork) \((X \leftarrow Z \to Y)\) aufweist, oder der Pfad \(X \to Y\) eine inverse Gabelung, also eine Kollision (collider) \((X \to C \leftarrow Y)\) aufweist, wobei ‘C’ nicht Z und auch keine Konsequenz von ‘C’ in Z ist (Pearl, 2009c, S. 17).
Im Fall der Verkettung und der Gabelung sind X und Y möglicherweise voneinander abhängig, werden aber unter Berücksichtigung von Z unabhängig (Pearl, 2009c, S. 17). Im Fall der Kollision sind X und Y möglicherweise unabhängig und haben beide eine Wirkung auf Z. Sobald Z (oder Konsequenzen aus Z) berücksichtigt werden, sind X und Y daher nicht mehr voneinander unabhängig (Pearl, 2009c, S. 17).
Ein weiteres von Pearl entwickeltes Prinzip im Hinblick auf das Ziel, Verzerrungen zu beseitigen ist das ‘Back-Door’-Kriterium. Wenn dieses Kriterium für eine Auswahl von Variablen Z in Bezug auf X und Y erfüllt wird, ist der kausale Effekt von X auf Y identifizierbar (Pearl, 2009a, S. 79).
Die systematische Umsetzung besteht darin, eine Auswahl von Variablen Z einzubinden, die alle falschen Pfade zwischen X und Y blockieren, keine Störungen auf direkte Pfade haben und keine neuen falschen Pfade erstellen (Pearl, 2009b, S. 339).
Um auf das Thema der ‘Unverfälschtheit’ zurück zu kommen. Wir verweisen in einem Beitrag (Bouncken, Ratzmann & Kraus, 2021) darauf, dass viele Forschungspraktiken darauf abzielen, mögliche Verzerrungen von OLS-Schätzern mithilfe robusterer Two-Stage-Least-Squares-Schätzer (2SLS-Schätzer, z.B. Antonakis et al., 2010) zu überprüfen.
Diese Methode wird jedoch auch eingesetzt, um vorhandene Ergebnisse zu rechtfertigen und scheitern, wenn nicht die richtigen Instrumente gefunden werden oder die Instrumente selbst nicht exogen sind. Neben dieser herkömmlichen Methode werden in der Datenanalyse zunehmend auch mathematische Algorithmen und adaptive Systeme aus den Methodenbereichen der ‘causal inference’ und des ‘causal structure learning’ eingesetzt.
Dabei geht es stark vereinfacht ausgedrückt darum, kausale Schlussfolgerung für die Zusammenhänge der vorliegenden Variablen zu finden. Beispielsweise verwendet der Algorithmus PC (Harris & Drton, 2013; Spirtes, Glymour & Scheines, 2000) bedingte Abhängigkeitstests (d-separation) zur Modellauswahl bei der grafischen Modellierung mit sogenannten Direct Acyclic Graphs (DAG) (Pearl, 2009a). Das Ergebnis kann aus Beobachtungsdaten Informationen über die Kausalstruktur ableiten, die Rückschlüsse auf die bedingte Abhängigkeit der untersuchten und teilweise auch unbeobachteten Quellen ermöglichen (Kalisch, Mächler, Colombo, Maathuis & Bühlmann, 2012).
Im Folgenden soll die Anwendung dieses Algorithmus PC demonstrieren, ob er geeignet ist, die zugrundeliegende Kausalstruktur, in dem bereits eingesetzten Datensatz von Antonakis (2011), aufzudecken. Hierfür wird im ersten Schritt eine Korrelationsmatrix aus den 10.000 Datensätzen gebildet, welche die Struktur der Daten (als ‘skeleton’ bezeichnet) aufzeigt. Im zweiten Schritt werden die möglichen Aussagen zur Kausalrichtung bestimmt und überprüft. In R können hierfür die Programm-Bibliotheken ‘pcalg’ (Hauser & Bühlmann, 2012; Kalisch et al., 2012) und ‘Rgraphviz’ (Hansen et al., 2021) verwendet werden. Den methodischen Hintergrund und das Vorgehen erläutert Hünermund (2020).
# Ansicht der Daten von Antonakis (2011)
data <- read.csv2("data/2slsdata.csv", header=TRUE)
# Erstellen einer Korrelations-Matrix
matrix <- list(C = cor(data), n = nrow(data))
matrix## $C
## q m n x y
## q 1.000000000 0.001361995 0.007305410 0.57975487 0.53986217
## m 0.001361995 1.000000000 -0.006388337 0.41161140 -0.15692978
## n 0.007305410 -0.006388337 1.000000000 0.40546038 -0.15544315
## x 0.579754870 0.411611400 0.405460382 1.00000000 0.04372556
## y 0.539862166 -0.156929780 -0.155443150 0.04372556 1.00000000
##
## $n
## [1] 10000library(pcalg)
library(Rgraphviz) ## Lade nötiges Paket: graph## Lade nötiges Paket: BiocGenerics## Lade nötiges Paket: parallel##
## Attache Paket: 'BiocGenerics'## Die folgenden Objekte sind maskiert von 'package:parallel':
##
## clusterApply, clusterApplyLB, clusterCall, clusterEvalQ,
## clusterExport, clusterMap, parApply, parCapply, parLapply,
## parLapplyLB, parRapply, parSapply, parSapplyLB## Die folgenden Objekte sind maskiert von 'package:stats':
##
## IQR, mad, sd, var, xtabs## Die folgenden Objekte sind maskiert von 'package:base':
##
## anyDuplicated, append, as.data.frame, basename, cbind, colnames,
## dirname, do.call, duplicated, eval, evalq, Filter, Find, get, grep,
## grepl, intersect, is.unsorted, lapply, Map, mapply, match, mget,
## order, paste, pmax, pmax.int, pmin, pmin.int, Position, rank,
## rbind, Reduce, rownames, sapply, setdiff, sort, table, tapply,
## union, unique, unsplit, which.max, which.min## Lade nötiges Paket: grid# Find the skeleton
skeleton <- skeleton(matrix, indepTest = gaussCItest,
labels = colnames(data), alpha = 0.01)
Rgraphviz::plot(skeleton)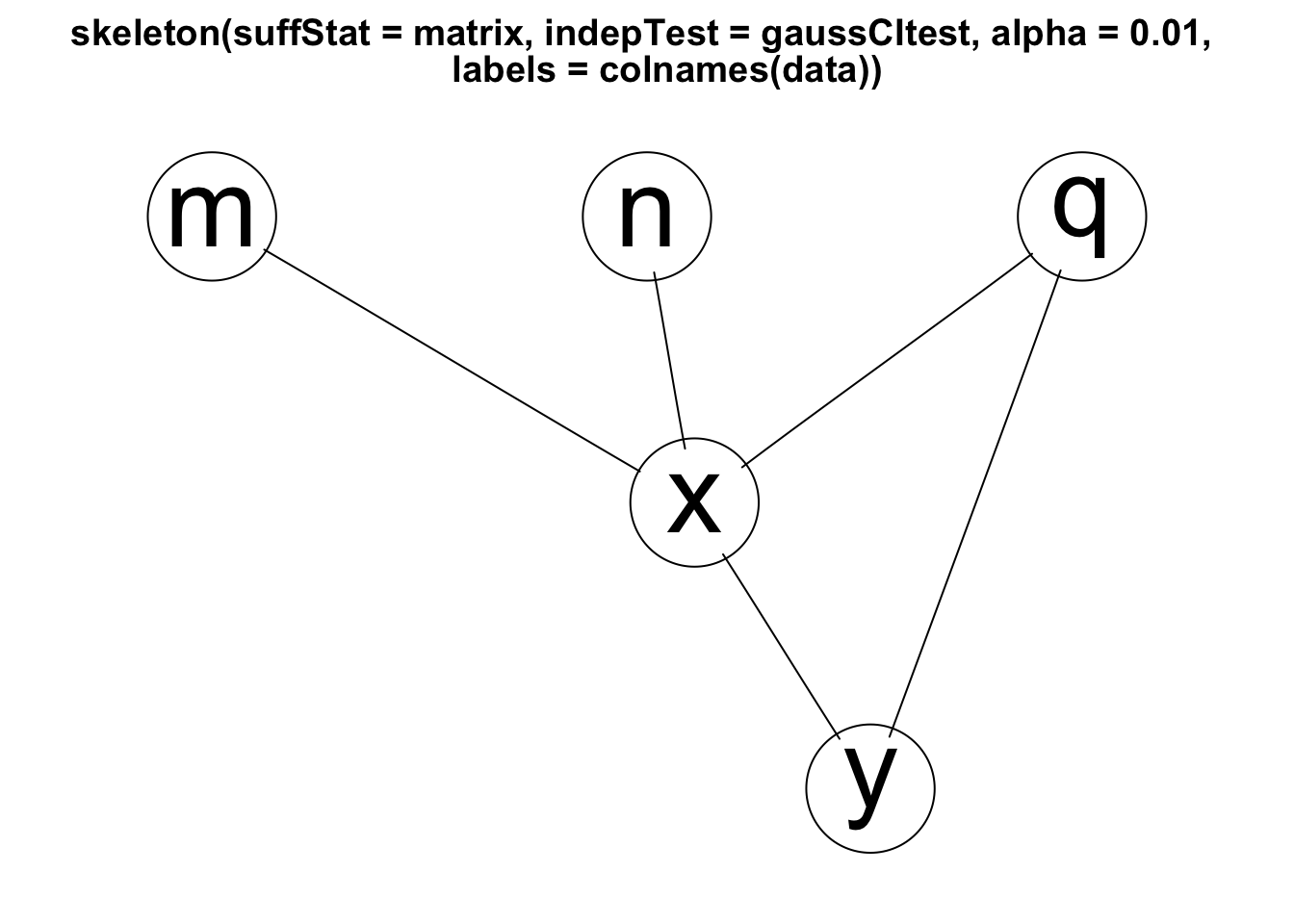
# Explore the causal structure
pc_graph <- pc(matrix, indepTest = gaussCItest, labels = colnames(data), alpha = 0.01)
Rgraphviz::plot(pc_graph)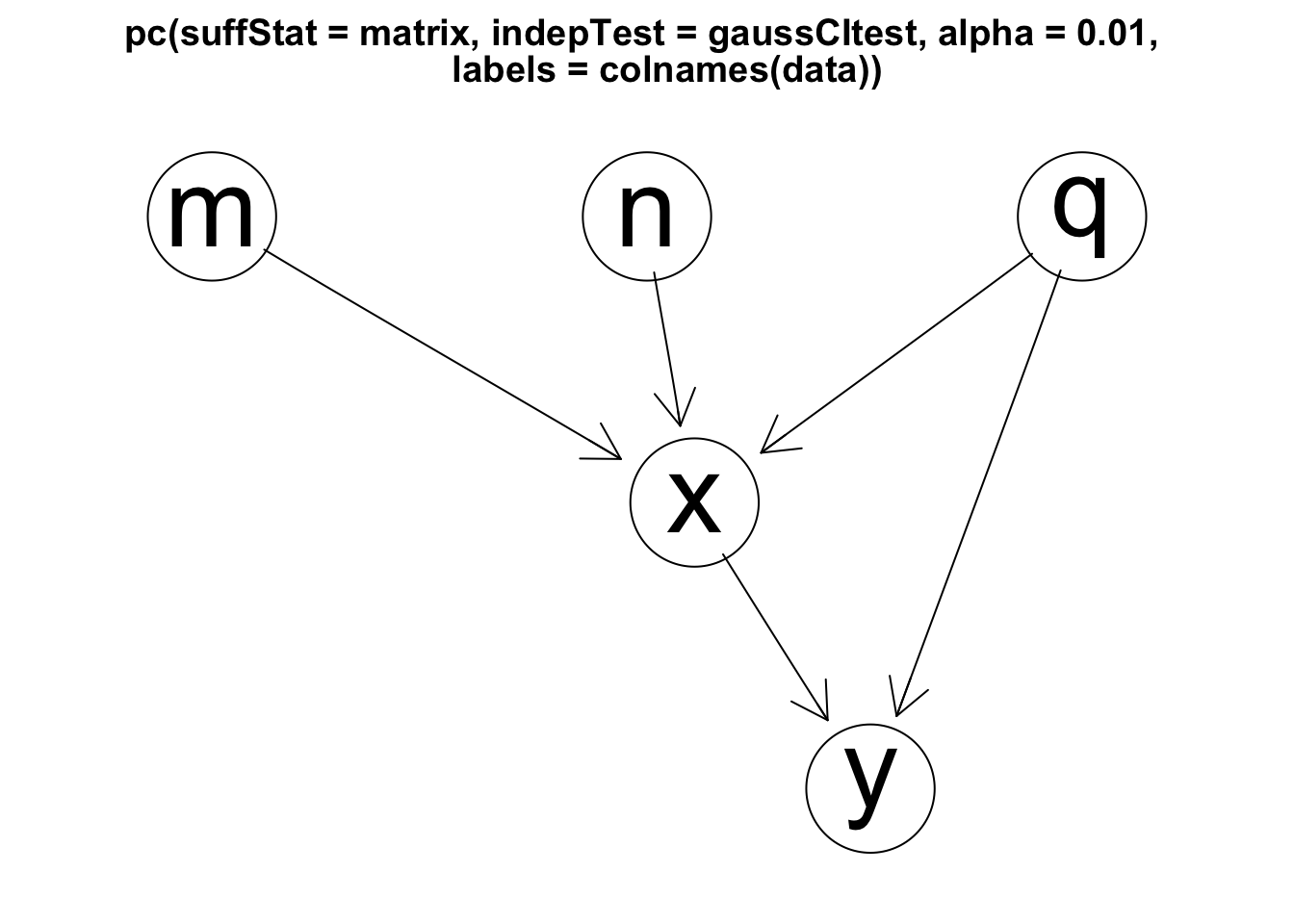
Im Ergebnis zeigt sich, dass sich die Variablen M, N und Q als voneinander unabhängig darstellen. M und N werden als Ursachen für X erkannt und Q als Ursache für X und Y. Zudem wird X als Ursache von Y aufgezeigt. Damit entspricht die herausgefundene Kausalstruktur exakt der als wahr vorgegebenen Datenstruktur von Antonakis (2011).
Zusammenfassend sei an dieser Stelle aufgezeigt, dass allein die Berechnung von Zusammenhangsmaßen zwischen Variablen und die Überprüfung hinsichtlich ihrer Signifikanz häufig nicht ausreicht, um angemessen über die Annahme oder Zurückweisung von Hypothesen zu entscheiden und daraus inhaltlich korrekte Aussagen zu formulieren.
Auf der anderen Seite sind aber auch Hinweise auf kausale Beziehungen möglich, selbst wenn die unabhängigen und abhängigen Variablen nicht zu unterschiedlichen Zeitpunkten erhoben wurden. Letztendlich entscheidet vielmehr das Verständnis, sowohl für die Datengrundlage, als auch für die angewandten Methoden über die Brauchbarkeit der abgeleiteten Ergebnisse
5.3 Querschnitt-Designs
Wie bereits dargestellt, bietet ein Querschnitt-Design auch einige Vorteile für die Forschung. Sie sind relativ sparsam in Hinblick auf die notwendigen Ressourcen und können relativ viele Forschungsfragen angemessen beantworten (Spector, 2019, S. 113). So können Sie gerade für relativ neue Forschungsthemen, in denen nur ein geringes Wissen über Variablen und Kontexte besteht, hilfreich sein. In diesem Fall können Aussagen gefunden werden, ob und wie Variablenpaare zusammenhängen und ob relevante Moderationen vorliegen. Diese Situation kennzeichnet insofern vor allem die explorativ ausgerichtete Forschung.
Außerdem könnten Ursachen, deren Zeitpunkt des Auftretens bereits in der Vergangenheit liegt, durch retrospektive Befragung einfließen und es können alternative Erklärungen für aktuell gegebene Ereignisse gesucht werden (Spector, 2019, S. 133). Werden Längsschnittstudien in neuen, noch unbekannten Forschungsgebieten durchgeführt, kann auch das Wissen um den richtigen Zeitrahmen, also den Zeitraum von der Ursache bis zum Eintreffen der Konsequenz, unbekannt sein.
Eine Längsschnittstudie bietet in diesem Kontext kaum Vorteile, insbesondere dann wenn ein falscher Zeitrahmen zu falschen Schlussfolgerungen darüber führt, wie stark der Zusammenhang zwischen Variablen wirklich ist (Spector, 2019, S. 134).
In einem angemessen dargestellten Querschnitt-Design sollte immer die systematische Analysestrategie erkennbar sein. Diese kann beispielsweise darin liegen, zuerst einen Zusammenhang zwischen X und Y darzustellen und dann mögliche (alternative) Erklärungen einzuschließen oder auszuschließen oder mögliche Kontext-Bedingungen in Form von Moderatoren aufzuzeigen (Spector, 2019, S. 135).
Außerdem können Zeitelemente auf andere Weise (z.B. eine theoretische Ereignishistorie) in die Analyse einbezogen werden. Die Grundlage für Schlussfolgerungen sollte auf logische Weise formuliert werden und alternative Erklärungen einbeziehen. Die aufgeführten Einschränkungen sollten durchdacht sein und Argumente für und gegen Einschränkungen aufzeigen. Es ist hilfreich, Vorschläge dafür zu geben, wie die Einschränkungen in zukünftigen Untersuchungen beseitigt werden könnten. Allein der Vorschlag, zukünftig experimentelle oder Längsschnitt-Designs zu verwenden ist dabei unangemessen und erzeugt beim Leser letztendlich nur die Frage, warum der Autor nicht das Design genutzt hat, dass er für notwendig hielt (Spector, 2019, S. 135).
Nicht zuletzt sollte Abstand von voreiligen Verallgemeinerungen der Aussagen genommen werden, die im speziellen Kontext des Forschungsthemas gelten. Anders formuliert, die Aussagen, dass ein Zusammenhang zwischen A und B existiert, dass möglicherweise auch A zu B führt oder sogar A als Ursache von B angesehen werden kann, sollten inhaltlich nicht überbewertet werden, da die Forschung immer nur einen kleinen Ausschnitt der wesentlich komplexeren Realität modelliert, wie die folgende Darstellung illustriert.