Kapitel 4 Datenanalyse
Als grundlegende Ziele der Forschung haben ich Beschreiben, Erklären und Nachweisen angesprochen. Zum Erklären und Nachweisen entwickelt der Forscher in der Regel zunächst eine Hypothese, das ist eine Aussage, die seine Vorstellung über einen Sachverhalt darstellt und die prinzipiell auch untersucht werden kann.
Ein Beispiel aus dem Bereich der wirtschaftswissenschaftlichen Theorien mag dies vielleicht verdeutlichen: Aus der Prinzipal-Agenten-Theorie (Jensen, 2000; Jensen & Meckling, 1976) sei die Annahme bekannt, dass Kooperationspartner nicht davor zurückschrecken, ihre eigenen egoistischen Interessen gegenüber dem Partner mit jedem Mittel durchzusetzen.
Aus der Literatur sei nun auch bekannt, dass in Beziehungen in denen opportunistisches Verhalten wahrgenommen oder erwartet wird, ein geringeres Vertrauen in den Kooperationspartner besteht. Weiterhin sei aus der Literatur bekannt, dass komplexe Verträge ausgearbeitet werden, um opportunistisches Verhalten zu reduzieren (Jones & Bouncken, 2008, S. 106). Der Kontext des Opportunismus bietet hier eine Grundlage für eine Hypothese über den Zusammenhang zwischen Vertragskomplexität und Vertrauen: Die resultierende Hypothese lautet demnach: ‘Steigende Vertragskomplexität steigert das Vertrauen in den Kooperationspartner.’
Eine Hypothese ist also ein Satz, der eine spezifische Aussage zu einem beobachtbaren Sachverhalt macht, der meistens aus einer Theorie abgeleitet ist und idealerweise für die gesamte Population (Grundgesamtheit) gelten soll.
Selbst wenn sich zeigt, dass dieser Satz in der Stichprobe zutrifft, besteht grundsätzlich die Möglichkeit, dass dieser Satz innerhalb der Stichprobe rein zufällig bestätigt wird, obwohl er sonst nicht richtig ist. In der traditionellen Statistik versucht man sich vor diesem Fehlschluss zu schützen, indem man der Hypothese eine sogenannte Nullhypothese gegenüberstellt, die den Inhalt der Hypothese negiert (Wendt, 1983).
Eine entsprechende Nullhypothese lautet demnach \(H_0\): ‘Es besteht kein Zusammenhang zwischen Vertragskomplexität und Vertrauen.’
Mit der eigentlichen Teststatistik bestimmt man dann die Wahrscheinlichkeit der Nullhypothese anhand der vorliegenden Daten. Ist die Wahrscheinlichkeit für die Richtigkeit der Nullhypothese gering und wird diese verworfen, wird dies als Beleg für die Akzeptanz ihrer Alternative (also der ursprünglichen Hypothese) angesehen.
An dieser Stelle muss angemerkt werden, dass innerhalb der Wissenschaften verschiedene Sichtweisen auf Wahrscheinlichkeit existieren. Die Auffassung von Wahrscheinlichkeit in der klassischen Statistik wird als ‘frequentistisch’ bezeichnet und Wahrscheinlichkeit wird dabei als Grenzwert einer relativen Häufigkeit dargestellt (Wendt, 1983):
\[p(X)= \lim_{n \to \infty} \frac {H\ddot{a}ufigkeit \: von \: X \: unter \: n \: Beobachtungen}{n}\]
Diese Wahrscheinlichkeit wird darüber bestimmt, wie häufig ein Ereignis in einer Population bzw. in einer Stichprobe aus der Population vorkommt. Dieses traditionelle Paradigma sieht Populationsparameter (wie z.B. Mittelwerte, Standardabweichungen, und Zusammenhangsmaße wie Korrelations- und Regressionskoeffizienten) als unbekannte, aber feste Größen der Grundgesamtheit an und das Ziel von Parameterschätzung ist es, Vertrauensintervalle für die Punktschätzung dieser Parameter in Stichproben zu finden (Rupp, Dey & Zumbo, 2004).
Der Test, der im Vorfeld formulierten Hypothese, besteht genau genommen darin, aufzuzeigen, dass die relative Häufigkeit der abgeleiteten Nullhypothese (das nämlich gar kein bzw. nur ein zufälliger Zusammenhang besteht) kleiner ist als die vorher festgelegte Wahrscheinlichkeit von \(\alpha\)=0.05. Wenn es ausreichend unwahrscheinlich ist, dass die Nullhypothese gilt, findet die eigentlich untersuchte Hypothese damit eine (indirekte) Bestätigung auf einem Signifikanzniveau von \(\alpha\) =0.05 und wird angenommen.
4.1 Exkurs: Logisches Schlußfolgern
Logisch gesehen, handelt es sich dabei um eine Entscheidung nach dem Schlussprinzip des sogenannten modus tollens (Wendt, 1983). Dabei handelt es sich um eine Regel der deduktiven Logik, die sich mit der korrekten Ableitung von Aussagen aus vorgegebenen anderen Aussagen befasst.
Aussagen werden in den Sprach- und Kognitionswissenschaften als Propositionen bezeichnet und bilden die kleinstmöglichen Wissenseinheiten ab, die entweder wahr oder falsch sein können (Westermann, 2000, S. 69).
In der Aussagenlogik werden Aussageformen, die Implikationen von Prämissen beinhalten als Schlussformen bezeichnet und stellen Regeln dar, nach denen man von wahren Aussagen zu anderen wahren Aussagen gelangen kann. Der modus tollens ist eine solche allgemeingültige Schlussformel:
\[[(A \to B) \wedge \neg B] \to \neg A \]
Er beinhaltet die implikative Verknüpfung von B folgt logisch aus A, formuliert mit \((A \to B)\). Wenn die Aussage A wahr ist, dann muss zwangsläufig auch die Aussage B wahr sein.
Zur Veranschaulichung solcher Schlussformen werden Wahrheitstabellen verwendet. Diese weisen aber auch darauf hin, dass logische Schlussformen nicht immer mit dem Alltagsverständnis von ‘wenn - dann’ Beziehungen einhergehen. So ist beispielsweise die Implikation B folgt logisch aus A \((A \to B)\) immer dann wahr, wenn A falsch ist. Dies betrifft in der Wahrheitstabelle die Zeilen 2 und 4. Definitionsgemäß ist die Implikation B folgt logisch aus A \((A \to B)\) nur dann als falsch anzusehen, wenn A wahr und B falsch ist (Westermann, 2000, S. 73).
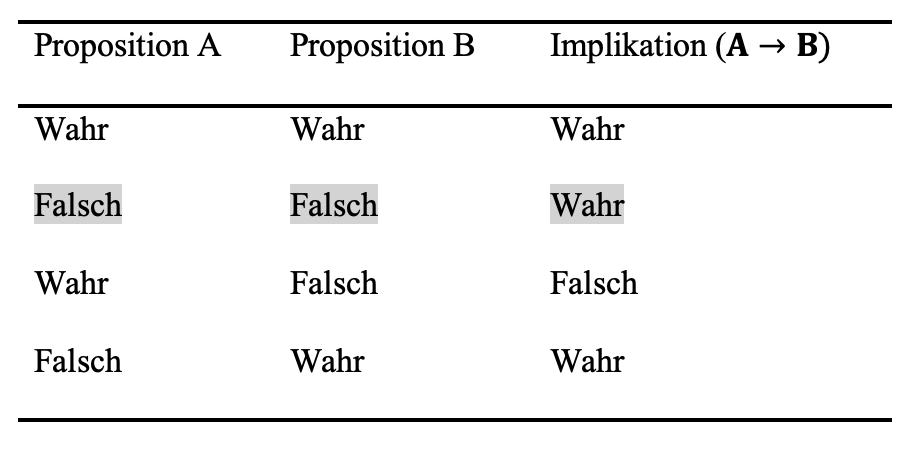
Der modus tollens regelt also den Geltungsbereich der Implikation B folgt logisch aus A ist wahr \((A \to B)\) und \((\wedge)\) die Aussage B ist falsch. Demnach schließt man aus der Unwahrheit von B unter der Bedingung, dass B folgt logisch aus A gilt \((A\to B)\), das A falsch ist (Zeile 2).
Übertragen auf das Problem der Hypothesenentscheidung ergibt sich die folgende Darstellung.
Die Hypothese ‘Steigende Vertragskomplexität steigert das Vertrauen in den Kooperationspartner’ soll Unterstützung finden. Dem gegenüber wird die Nullhypothese \((H_0)\) getestet, dass gar kein Zusammenhang besteht. Die Nullhypothese beinhaltet nun auch spezifische Annahmen über die Verteilung (Mittelwert, Standardabweichung) und Zusammenhangsmaße (Kovarianz) der Daten in der Stichprobe \((D_0)\). Entsprechend der Normalverteilungsannahme wäre dies: das Zusammenhangsmaß ist normalverteilt und hat einen Mittelwert von Null (kein Zusammenhang).
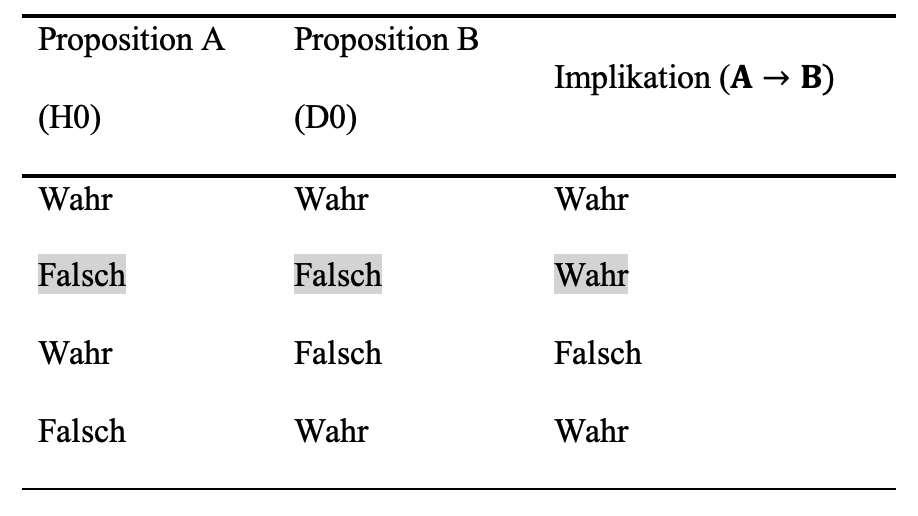
Aus Zeile 1 der Wahrheitstabelle können wir folgendes entnehmen: die Implikation B folgt logisch aus A ist wahr \((A\to B)\), \(H_0\) (die Nullhypothese) und \(D_0\) (das damit erwartete mittlere Zusammenhangsmaß in \(D_0\) von Null) sind wahr.
Zeile 2 zeigt auf: Die Implikation B folgt logisch aus A ist wahr \((A\to B)\), wobei \(H_0\) falsch ist (es ist also die falsche Nullhypothese) und \(D_0\) ist ebenso falsch (das Zusammenhangsmaß in \(D_0\) ist ungleich Null).
In Zeile 3 ist: Die Implikation B folgt logisch aus A \((A\to B)\) definitionsgemäß falsch, wenn A (die Nullhypothese \(H_0\)) wahr und B falsch ist (also ein Zusammenhangsmaß ungleich Null aufweist).
Aus Zeile 4 lässt sich ablesen, dass: Die Implikation B folgt logisch aus A ist auch wahr \((A \to B)\), wenn A (die Nullhypothese \(H_0\)) falsch und B (Zusammenhangsmaß gleich Null) wahr ist.
Nach dem modus tollens wird geschlossen, dass wenn das Zusammenhangsmaß ungleich Null ist und unter der Bedingung, dass B folgt logisch aus A gilt \((A\to B)\), dass die Nullhypothese falsch ist. (Dies entspricht der zweiten Zeile der Wahrheitstabelle).
Auch Forscher unterliegen häufiger erheblichen Schwierigkeiten mit Folgerungen, die dem modus tollens entsprechen und sie schließen von der Zurückweisung der Nullhypothese (A ist falsch) auf ein Zusammenhangsmaß das ungleich Null ist (B ist unwahr) (Anderson, 1996, S. 304–308), was aber nicht logisch zwingend (Westermann, 2000, S. 80) und in Zeile 3 dargestellt ist.
Mit anderen Worten, wenn die Implikation B folgt logisch aus A \((A\to B)\) gilt (Zeilen 1, 2 und 4) und wenn B falsch ist (Zeilen 2), lässt sich daraus die Falschheit von A ableiten (Modus tollens).
Ist die Aussage, dass die Verteilung der Daten \(D_0\) der Annahme aus \(H_0\) folgen, falsch (bzw. ist die Wahrscheinlichkeit zu gering), so wird entschieden, dass die Nullhypothese \(H_0\) falsch ist und ‘Quoniam tertium non datur’ damit darf die Alternativhypothese (als ihr Gegenteil) als richtig angesehen werden (Wendt, 1983). Dies folgt dem logischen Grundprinzip, nach dem für eine Aussage nur die Aussage selbst oder ihr Gegenteil gelten kann. Eine dritte Möglichkeit, etwas, das weder die Aussage selbst noch ihr Gegenteil ist, kann es paradigmatisch nicht geben.
Zusammenfassend wurde hier abgeleitet, wie der Gewinn neuer Erkenntnisse über die Falsifikation, also das Zurückweisen der Nullhypothese erfolgt: \([(\neg H_0) \to H_A]\). Wenn die Nullhypothese nicht verworfen werden kann, kann daraus jedoch nicht logisch geschlossen werden, dass die Nullhypothese ‘wahr’ ist (Wendt, 1983).
4.2 Rechtliche Rahmenbedingungen
In meinem letzten Vortrag hatte ich die empirische Forschung als wissenschaftliche Methodik vorgestellt, die auch in wirtschaftswissenschaftlichen Fachgebieten genutzt wird um zielgerichtete Handlungen und Entscheidungen im betrieblichen Geschehen zu untersuchen. Dabei habe ich die Ebenen des Beschreibens, Erklärens und Prognostizierens als Methoden der empirischen Forschung angesprochen und die Beobachtung, das Interview und die Fragebogenerhebungen als Verfahren der Datenerhebung vorgestellt.
Neben der Stichprobenauswahl wurden die Objektivität, die Reliabilität und die Diskriminanz-Validität als zentrale Gütekriterien von Datenerhebungenverfahren vorgestellt.
Anhand der strukturierten Fragebogenforschung, wurde das Problem theoretischer Konstrukte angesprochen, welche nicht die Realität an sich, sondern eine Vorstellung der Wirklichkeit darstellen. Außerdem wurde die Auswahl der Untersuchungsteilnehmer als mögliche Einschränkung vorgestellt, um die Ergebnisse aus der Stichprobe auf die Grundgesamtheit zu übertragen. Zudem möchte ich an dieser Stelle auf ein weiteres mögliches Selektionskriterium hinweisen. Ein typisches Problem, warum angesprochene Untersuchungsteilnehmer fehlende Bereitschaft für Befragungen zeigen können, ist auch der Umgang mit personenbezogenen oder personenbeziehbaren Daten. In allen Datenerhebungen (wie z.B. Umfragen) sind die Teilnehmer durch eine Datenschutzerklärung über den Zweck, die Form und den Umfang der Erhebung und Verarbeitung zu informieren und müssen dieser auch in Form einer Einwilligungserklärung zustimmen.
Beispiel für eine Einwilligungserklärung:
Auf den folgenden Seiten wollen wir Ihnen ein paar Fragen zu dem Thema ‘Digitalisierung’ stellen. Ziel unserer Befragung ist es, den Einsatz von Digitalisierung in Unternehmen besser bewerten zu können. Vor der Befragung werden wir nähere Informationen zu Ihrer Person (Firma, Alter, Geschlecht, Position im Unternehmen etc.) abfragen.
Die Befragungsdaten werden ausschließlich zu wissenschaftlichen Zwecken genutzt und es wird sichergestellt, dass ihre personenbezogenen und personenbeziehbaren Daten nicht mit Ihren Angaben in Verbindung gebracht werden können.
Die Teilnahme an dieser Umfrage ist ohne Nennung Ihres Namens und ohne Registrierung möglich. Vor Abschluss der Befragung erhalten Sie die Möglichkeit, Ihre Angaben in einer Gesamtansicht zu prüfen oder zu ändern. Gemäß den datenschutzrechtlichen Bestimmungen haben Sie gegenüber dem Informationsträger das Recht auf Auskunft sowie Löschung Ihrer personenbezogenen Daten. Sie können die Einwilligungserklärung jederzeit widerrufen.
Insbesondere wenn Datenerhebungen über Webserver organisiert werden, kann die Einhaltung solcher Vereinbarungen den Forscher bei der Aufbereitung und Aggregation der Daten auf Datenbankebene vor eine große Herausforderung stellen (Schmitz & Yanenko, 2014).Typischerweise werden solche Daten in relationalen Datenbanken organisiert.
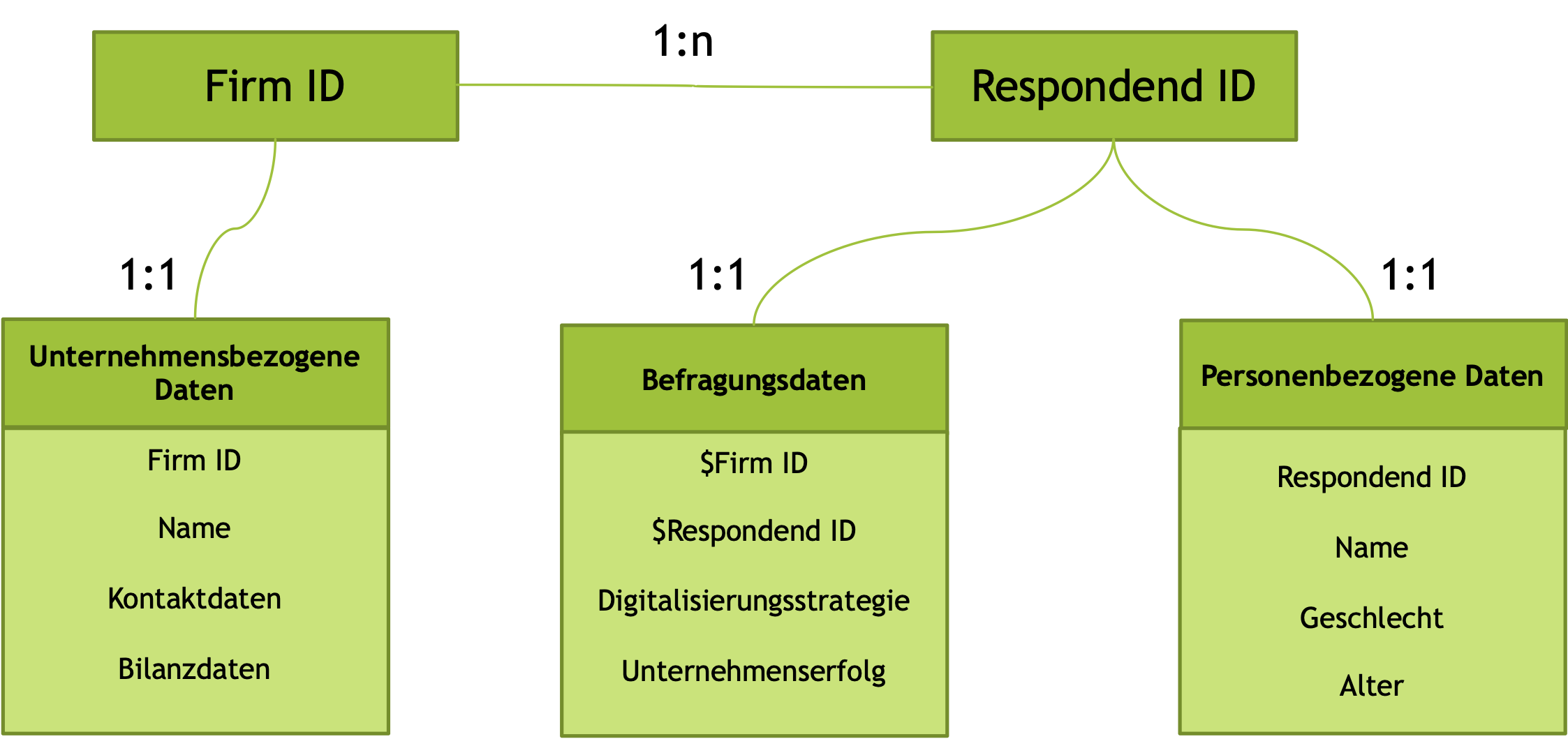
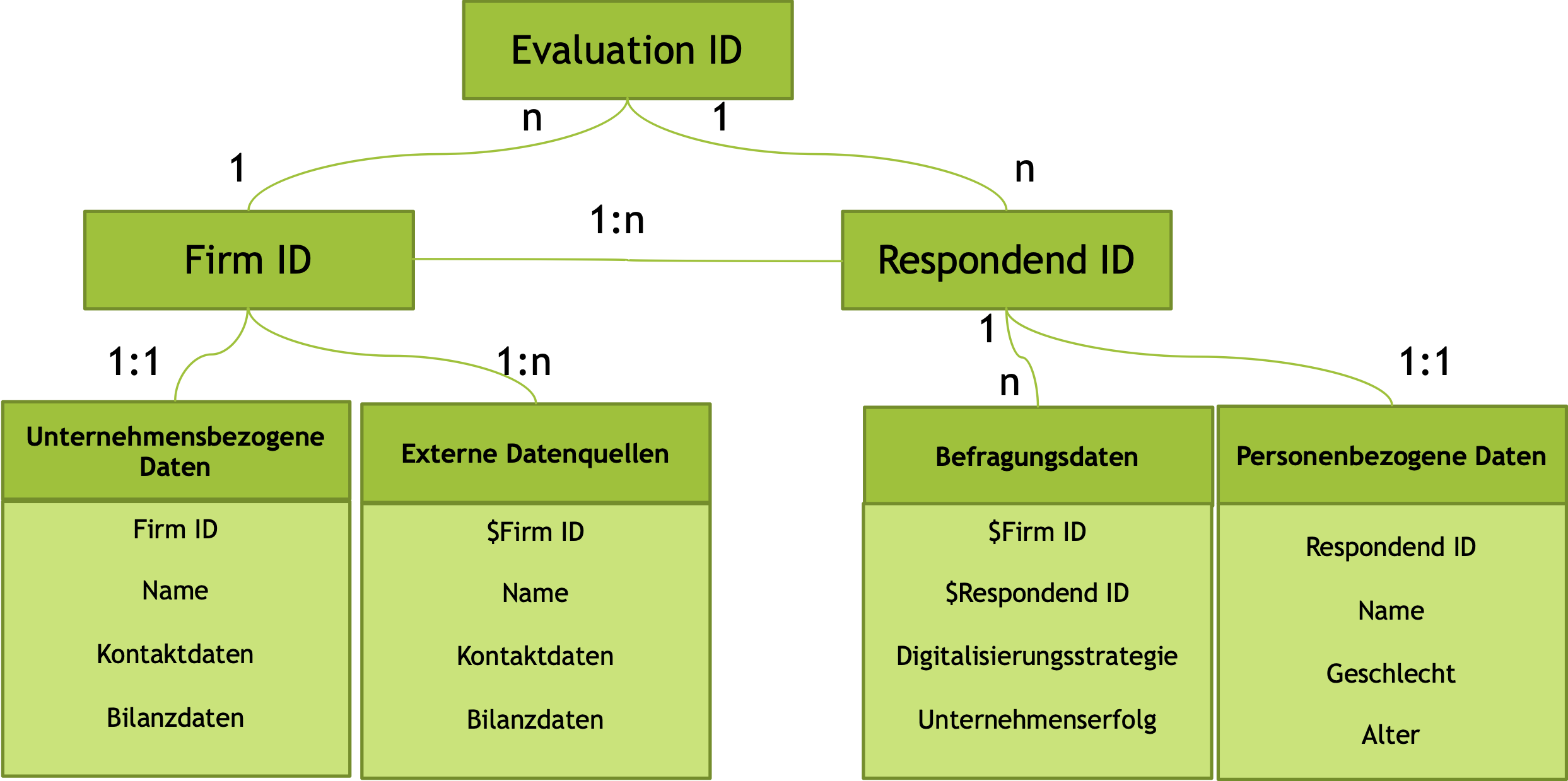
In diesem relativ einfachen Beispiel wird ein Fragebogen in fünf Tabellen organisiert, die durch spezifische Codes verbunden sind. Jedes befragte Unternehmen erhält dabei eine einmalig generierte spezifische ‘Firm ID’, der alle Befragungen dieses Unternehmens zugewiesen werden. Gleiches gilt für die befragten Teilnehmer. Jedem Befragten wird eine einmalig generierte ‘ID’ zugewiesen. Die eigentlichen Befragungsdaten müssen dementsprechend mit beiden ‘ID’s’ verbunden sein.
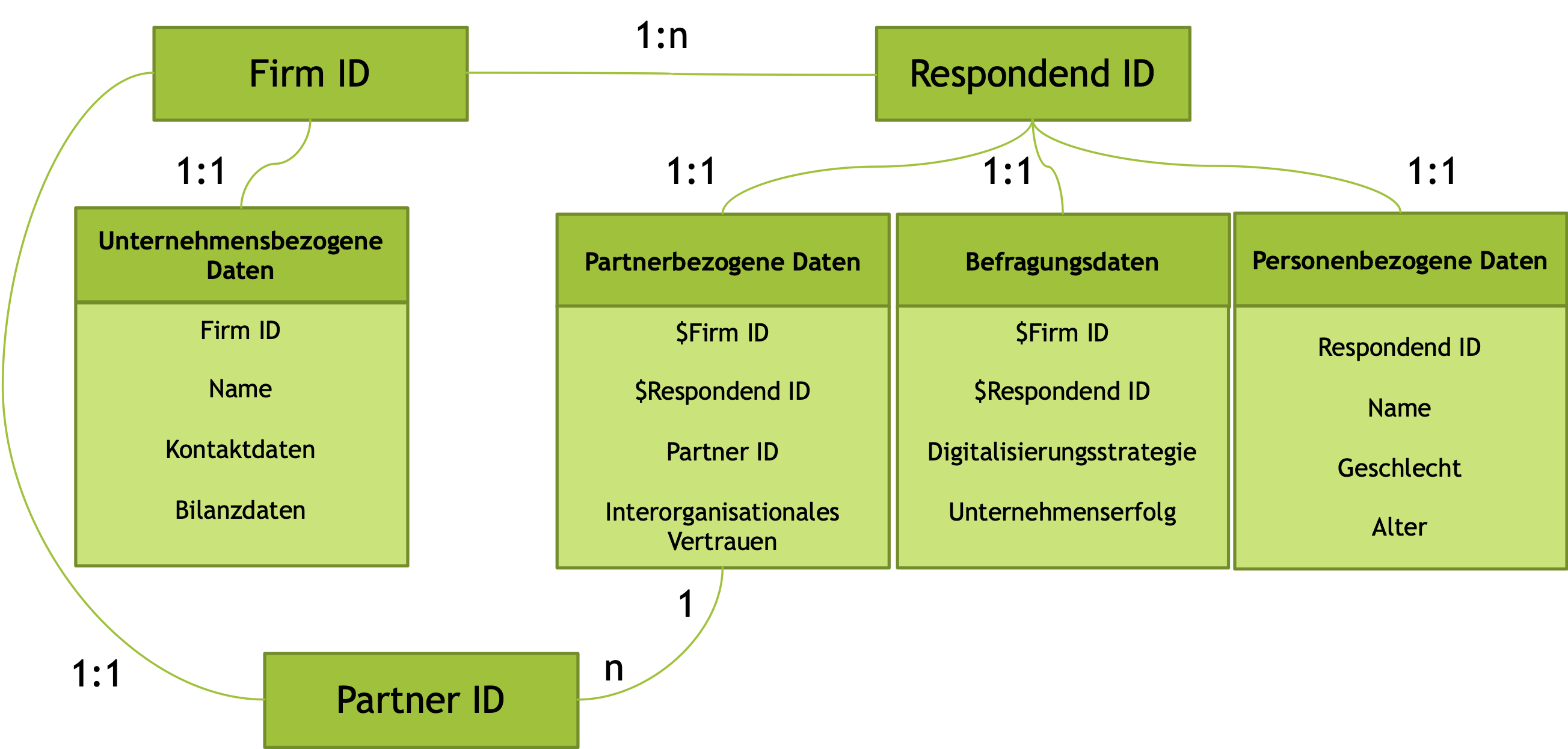
Werden zusätzlich Partnerunternehmen befragt, resultieren daraus weit komplexere Verknüpfungen, da bspw. das Partnerunternehmen selbst auch als befragtes Unternehmen in einer Erhebung angesprochen werden kann.
Gleiches gilt, wenn mehrere Erhebungszeitpunkte existieren oder geplant sind. Prospektive Überlegungen zur Struktur der Daten sind extrem vorteilhaft, weil die rückwirkende Zuordnung von Daten-Verknüpfungen nicht nur mit einem enormen Aufwand, sondern auch mit einer hohen Fehleranfälligkeit verbunden sind.
4.3 Datenaufbereitung
Daten liegen uns gewöhnlich in Form von Datentabellen vor. In dieser Form weist jede Zeile auf eine Befragung hin. Die erste Spalte beinhaltet eine ID, durch die dieser einzelne Fall Verknüpfungen mit anderen Datentabellen aufweisen kann.
Die folgenden Spalten J1 bis J9 weisen hier auf den Fragebogenabschnitt ‘J - Digitale Orientierung unseres Unternehmens’ und die darin erhobenen Items J1 bis J9 hin. Bei den dargestellten Daten handelt es sich um reale Erhebungsdaten aus dem Jahr 2019. Der Befragte mit der ID 195 hat demnach auf die Aussage ‘Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen’ mit ‘5’ für ‘voll zutreffend’ geantwortet. Der Befragte mit der ID 201 weist auf leere Zellen hin. Dieser Befragte hat also (egal aus welchen Gründen) an dieser Stelle keine Angaben gemacht.
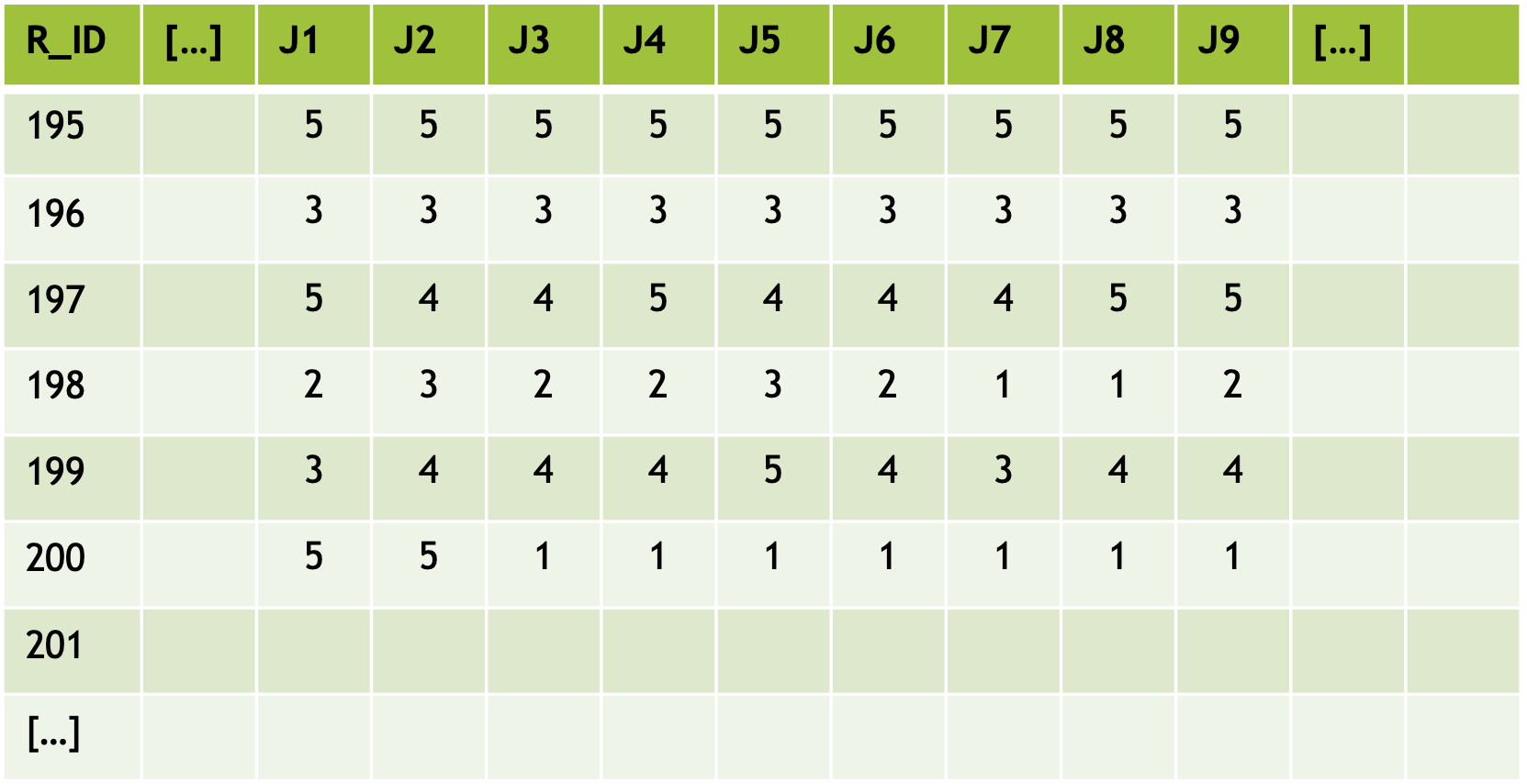
Betrachten wir die Tabelle Spaltenweise können andere Aussagen getroffen werden. So kann aufgezeigt werden, dass 57 Prozent die Aussage ‘Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen’ mit ‘eher’ oder ‘voll zutreffend’ beantwortet haben. Nur 14 Prozent der Befragten hat die Aussage mit ‘eher nicht’ oder ‘nicht zutreffend’ beantwortet.
Spaltenweise können weitere statistische Kennwerte bestimmt werden. Das arithmetische Mittel ist das gebräuchlichste Maß zu Kennzeichnung der zentralen Tendenz (Bortz, 1993, S. 38). Dabei wird die Summe der Einzelwerte in Relation zur Anzahl der Werte bestimmt.
\[ \overline{x}= \frac {1}{n} \sum_{k=1}^{n} x_k\]
Es wird bereits hier deutlich, dass die ursprüngliche Skala (von ‘trifft nicht zu’ bis ‘trifft vollständig zu’) keine geeignete Interpretationsmöglichkeit bietet. Die Aussage ‘Wir sind ständig auf der Suche nach neuen digitalen Geschäftsideen’ wird im Durchschnitt mit einem Wert von 3.83 beantwortet wobei die Skala von 1 bis 5 reicht.
In der Idealform werden Items so formuliert bzw. skaliert, dass der durchschnittliche Wert in großen Zufallsstichproben dem Skalenmittelwert entspricht. Das zweite Item J2 ‘Wir arbeiten daran, neue digitale Geschäftsmodelle zu entwickeln’ wurde beispielsweise von keinem der 7 Befragten mit trifft nicht zu oder trifft eher nicht zu beantwortet.
Die daraus resultierenden Einschränkungen der Variabilität in den Antworten, kann später zu Problemen in bestimmten Analyseverfahren beitragen.
Die Varianz \((s^2 bzw. \sigma^2)\) gehört zu den gebräuchlichsten Maßen zur Kennzeichnung der Variabilität der Verteilung und ergibt sich aus der Summe der quadrierten Abweichungen aller Messwerte vom quadratischen Mittel, dividiert durch die Anzahl der Messwerte (Bortz, 1993, S. 41).
\[ \sigma^2 = s^2 = \sum_{i=1}^{n} (x_i-\overline{x})^2\]
Die Standardabweichung (auch als Streuung bezeichnet) ergibt sich aus der Wurzel der Varianz und beschreibt die durchschnittliche Abweichung vom arithmetischen Mittel.
\[ \sigma = sd = \sqrt {\sigma^2}\]
4.4 Exkurs: Datenanalysen in R
Im Folgenden werde ich immer wieder verschiedene Beispiele und Anwendungen vorstellen. Damit diese von Ihnen Nachvollzogen werden können, setzen wir die Statistikumgebung ‘R’ ein.
‘R’ ist eine Open-Source Programmierungsumgebung zur Datenanalyse und Visualisierung, die sich zu einem Quasi-Standard für statistische Analysen entwickelt hat. Hierfür werden fortlaufend neue Programmpakete bzw. Bibliotheken mit Funktionen (sogenannte Packages) entwickelt, die frei zugänglich veröffentlicht werden und die es ermöglichen, spezifische Methoden zu entwickeln und zu verwenden (Racine & Hyndman, 2002). Um diese Möglichkeiten zu nutzen ist die Installation von ‘R’ (R Core Team, 2021) oder RStudio (RStudio Team, 2020) unverzichtbar. Grundlegende Kenntnisse im Umgang mit ‘R’ sind dabei extrem vorteilhaft, jedoch nicht zwingend notwendig.
4.4.1 Zusammenhangsmaße
Die Kovarianz (covariance) ist eine Messung des Zusammenhanges (association or relationship) zweier Variablen (Kenny, 2004, S. 17) oder anders formuliert die Kovarianz misst die gemeinsame (Ko)-Variation der Werte eines Variablenpaares (Dolic, 2010, S. 205). Mathematisch wird die Kovarianz als Erwartungswert der Abweichungen vom jeweiligen Populationsmittelwert zweier Variablen definiert (Kenny, 2004):
\[ E[(X-\mu_X)(Y-\mu_X)]\]
Dabei stellt E die Erwartung dar und die Populationsmittelwerte sind für Variable X durch \(\mu_X\) und für die Variable Y durch \(\mu_Y\) bezeichnet.
Zwei gebräuchliche Schreibweisen zur Bezeichnung von Kovarianzen sind: cov(x,y) und \(\sigma_{XY}\) (sigma). Eine unverzerrte Stichprobenschätzung der Kovarianz ergibt sich in Zufallsstichproben nach der dargestellten Gleichung, wobei \(M_X\) und \(M_Y\) die Stichprobenmittelwerte und N die Stichprobengröße darstellen (Kenny, 2004):
\[cov(x,y)=\frac{\sum(X-M_X)(Y-M_Y)}{N-1}\]
Aus unserer ursprünglichen Datentabelle, welche (die ID ausgeschlossen) neun Variablen J1 bis J9 beinhaltet, ergeben sich dem entsprechend 9x9 mögliche Kovarianzen, die sich in Form einer Kovarianzmatrix darstellen lassen. Dabei gilt per Definition, dass die Kovarianz einer Variablen mit sich selbst gleich der Varianz der Variable
\[cov(x,x)=var(x)=\sigma^2_x\] und die Kovarianz von Variablenpaar x - y gleich der Kovarianz von y - x ist.
\[cov(x,y)=cov(y,x)\]
J1 <- c(5,3,5,2,3,5)
J2 <- c(5,3,4,3,4,5)
J3 <- c(5,3,4,2,4,1)
J4 <- c(5,3,5,2,4,1)
J5 <- c(5,3,4,3,5,1)
J6 <- c(5,3,4,2,4,1)
J7 <- c(5,3,4,1,3,1)
J8 <- c(5,3,5,2,4,1)
J9 <- c(5,3,5,2,4,1)
data <- cbind(J1,J2,J3,J4,J5,J6,J7,J8,J9)
round (cov(data), digits=2)## J1 J2 J3 J4 J5 J6 J7 J8 J9
## J1 1.77 1.0 0.43 0.67 -0.1 0.43 0.97 0.67 0.67
## J2 1.00 0.8 0.20 0.20 0.0 0.20 0.40 0.20 0.20
## J3 0.43 0.2 2.17 2.33 2.1 2.17 2.23 2.33 2.33
## J4 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67
## J5 -0.10 0.0 2.10 2.20 2.3 2.10 1.90 2.20 2.20
## J6 0.43 0.2 2.17 2.33 2.1 2.17 2.23 2.33 2.33
## J7 0.97 0.4 2.23 2.47 1.9 2.23 2.57 2.47 2.47
## J8 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67
## J9 0.67 0.2 2.33 2.67 2.2 2.33 2.47 2.67 2.67Für die resultierende Kovarianzmatrix ergibt sich, dass die Diagonale von links oben nach rechts unten die Auto-Kovarianzen (also die Varianzen) darstellt. Die darüber und darunter liegenden Kovarianzen liegen in gespiegelter Form vor. Sollen Zusammenhänge zwischen Variablen nicht nur aufgezeigt, sondern hinsichtlich ihrer Signifikanz beurteilt werden, werden üblicherweise Korrelations-Matrizen anstelle der Kovarianz-Matrizen bestimmt. Die Korrelationskoeffizienten können hinsichtlich der Nullhypothese getestet werden, dass die wahre Korrelation gleich einem Wert von Null ist.
data<- data.frame(data)# Signifikanztest für Korrelationskoeffizienten bestimmen
cor.test(data$J1, data$J2, use = "pairwise.complete.obs",
method = c("pearson", "kendall", "spearman"))##
## Pearson's product-moment correlation
##
## data: data$J1 and data$J2
## t = 3.1109, df = 4, p-value = 0.03584
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.09326324 0.98221144
## sample estimates:
## cor
## 0.8411582# Gesamte Korrelations-Matrix erstellen und die Ausgabe auf
# zwei Kommastellen reduzieren
round (cor(data), digits=2)## J1 J2 J3 J4 J5 J6 J7 J8 J9
## J1 1.00 0.84 0.22 0.31 -0.05 0.22 0.45 0.31 0.31
## J2 0.84 1.00 0.15 0.14 0.00 0.15 0.28 0.14 0.14
## J3 0.22 0.15 1.00 0.97 0.94 1.00 0.95 0.97 0.97
## J4 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00
## J5 -0.05 0.00 0.94 0.89 1.00 0.94 0.78 0.89 0.89
## J6 0.22 0.15 1.00 0.97 0.94 1.00 0.95 0.97 0.97
## J7 0.45 0.28 0.95 0.94 0.78 0.95 1.00 0.94 0.94
## J8 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00
## J9 0.31 0.14 0.97 1.00 0.89 0.97 0.94 1.00 1.00Nur erwähnt sei an dieser Stelle, dass auch andere spezifische Zusammenhangsmaße existieren. Partialkorrelationen sind eine spezifische Form, bei welcher der Zusammenhang zwischen einem Variablenpaar durch das Auspartialisieren des Einflusses von Drittvariablen, z.B. mit der ‘R’-Programm-Bibliothek ‘ppcor’ (Kim, 2015), bestimmt wird. Wir werden später darauf zurückkommen.
# Partial-Korrelations-Matrix erstellen
# (vgl. https://www.statology.org/partial-correlation-r/)
library (ppcor)## Lade nötiges Paket: MASSpr <- pcor(data)
round(pr$estimate, digits = 2)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1.00 -0.07 0.67 -0.62 0.09 0.67 0.46 -0.62 -0.62
## [2,] -0.07 1.00 -0.25 0.27 -0.82 -0.25 0.30 0.27 0.27
## [3,] 0.67 -0.25 1.00 0.96 0.04 -1.00 -0.80 0.96 0.96
## [4,] -0.62 0.27 0.96 1.00 -0.07 0.96 0.79 -1.00 -1.00
## [5,] 0.09 -0.82 0.04 -0.07 1.00 0.04 0.63 -0.07 -0.07
## [6,] 0.67 -0.25 -1.00 0.96 0.04 1.00 -0.80 0.96 0.96
## [7,] 0.46 0.30 -0.80 0.79 0.63 -0.80 1.00 0.79 0.79
## [8,] -0.62 0.27 0.96 -1.00 -0.07 0.96 0.79 1.00 -1.00
## [9,] -0.62 0.27 0.96 -1.00 -0.07 0.96 0.79 -1.00 1.004.4.2 Prognose von Variablenwerten mittels Regressionsrechnung
Zunächst möchte ich auf eine Methode für den Nachweis von Zusammenhängen, Prognosen und Ursache-Wirkungs-Beziehungen (Kausalzusammenhängen) eingehen. Die Regressionsanalyse zählt zu den häufigsten statistischen Anwendungen, um Zusammenhänge zwischen metrischen (idealerweise intervallskalierten) Variablen zu beschreiben und zu prüfen. Üblicherweise wird dabei versucht, die unterschiedlichen Ausprägungen einer Variablen (meist als abhängige Variable bezeichnet) durch eine oder mehrere andere Variablen zu erklären (Dolic, 2010). Die abhängige Variable Y wird also als mathematische Funktion von X angesehen.
\[Y=f(X)\] Folgt man dabei der Annahme, dass die Beziehung zwischen X und Y deterministisch ist, kann diese Beziehung durch die allgemeine mathematische Gleichung: \[y=a + b \cdot x\] beschrieben werden (Bortz, 1993, S. 157). Durch diese lineare Gleichung ergibt sich jeder Wert der abhängigen Variable Y aus der Summe von a (dem Schnittpunkt der Geraden mit der y-Achse) und dem Produkt des Steigungskoeffizienten b mit dem Wert der unabhängigen Variable X (Bortz, 1993, S. 157).
Mit anderen Worten: durch das Wissen um a und b und die Funktionsgleichung kann für beliebige Werte x ein korrespondierendes y berechnet werden. Der Steigungskoeffizient b gibt darüber Auskunft, ob sich die ergebenden Werte in Y, bei ansteigenden Werten in X, vergrößern, verkleinern oder konstant bleiben.
a <- 2.5
b <- 0.5
x <- 0:5
y <- a+b*x
cbind(x,y)## x y
## [1,] 0 2.5
## [2,] 1 3.0
## [3,] 2 3.5
## [4,] 3 4.0
## [5,] 4 4.5
## [6,] 5 5.0plot(x,y,type="l",xlim=c(0,5),ylim=c(0,5),
xlab="X-Variable",ylab="Y= 2.5 + 0.5X",
panel.first=grid(), col="blue")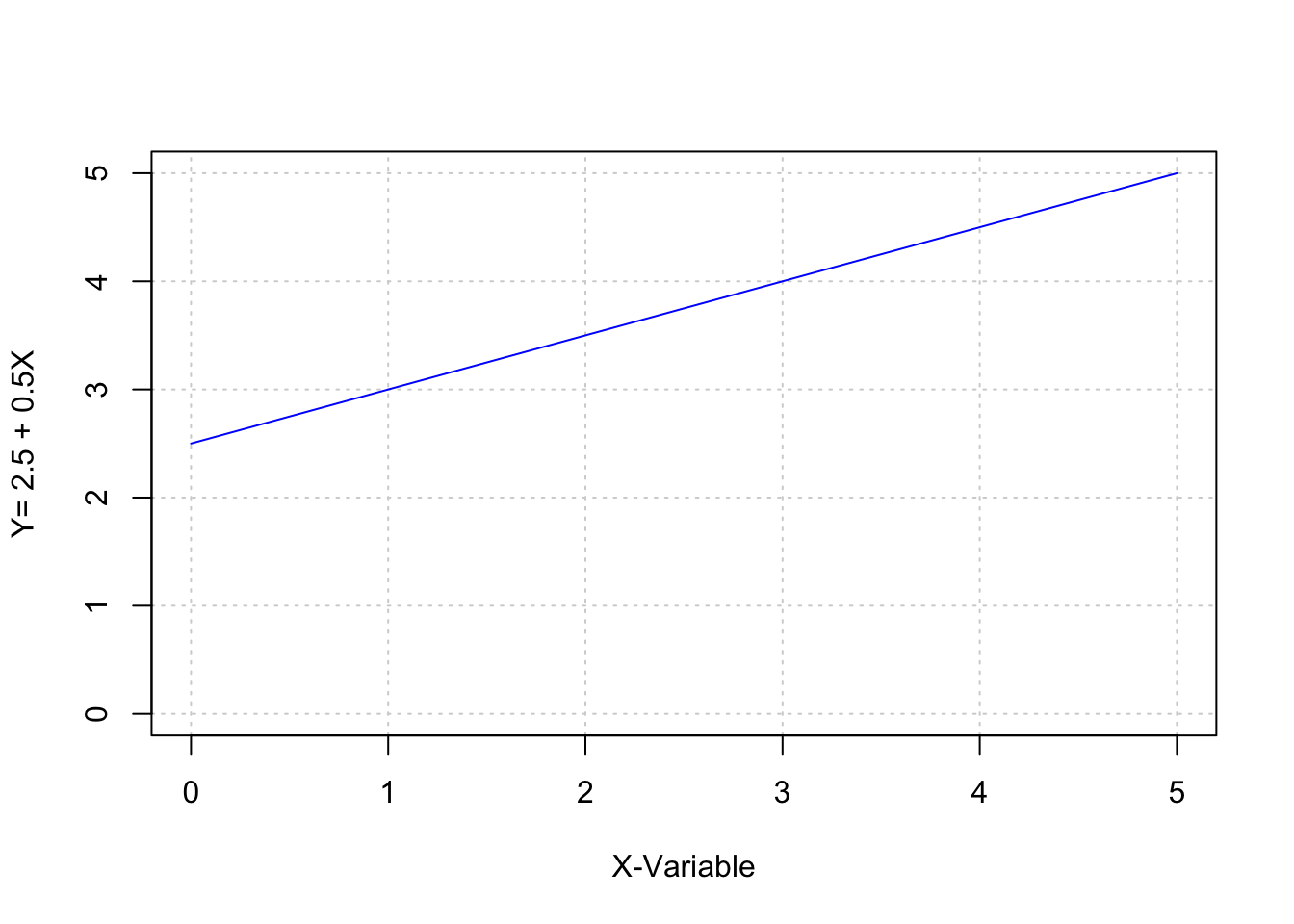
a <- 2.5
b <- -0.5
x <- 0:5
y <- a+b*x
cbind(x,y)## x y
## [1,] 0 2.5
## [2,] 1 2.0
## [3,] 2 1.5
## [4,] 3 1.0
## [5,] 4 0.5
## [6,] 5 0.0plot(x,y,type="l",xlim=c(0,5),ylim=c(0,5),
xlab="X-Variable",ylab="Y= 2.5 + (-0.5)X",
panel.first=grid(), col="blue")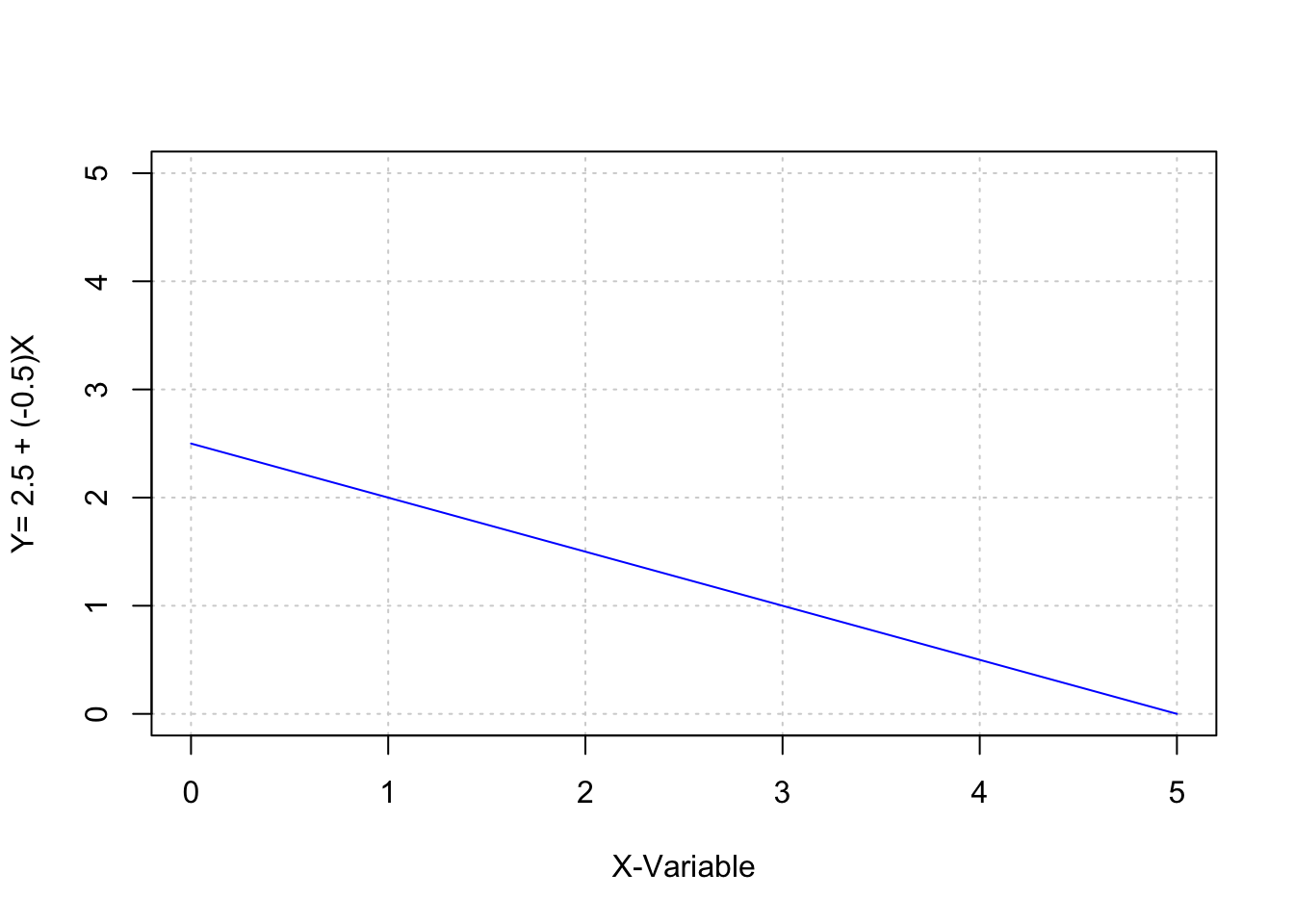
a <- 2.5
b <- 0
x <- 0:5
y <- a+b*x
cbind(x,y)## x y
## [1,] 0 2.5
## [2,] 1 2.5
## [3,] 2 2.5
## [4,] 3 2.5
## [5,] 4 2.5
## [6,] 5 2.5plot(x,y,type="l",xlim=c(0,5),ylim=c(0,5),
xlab="X-Variable",ylab="Y= 2.5 + 0.0 X",
panel.first=grid(), col="blue")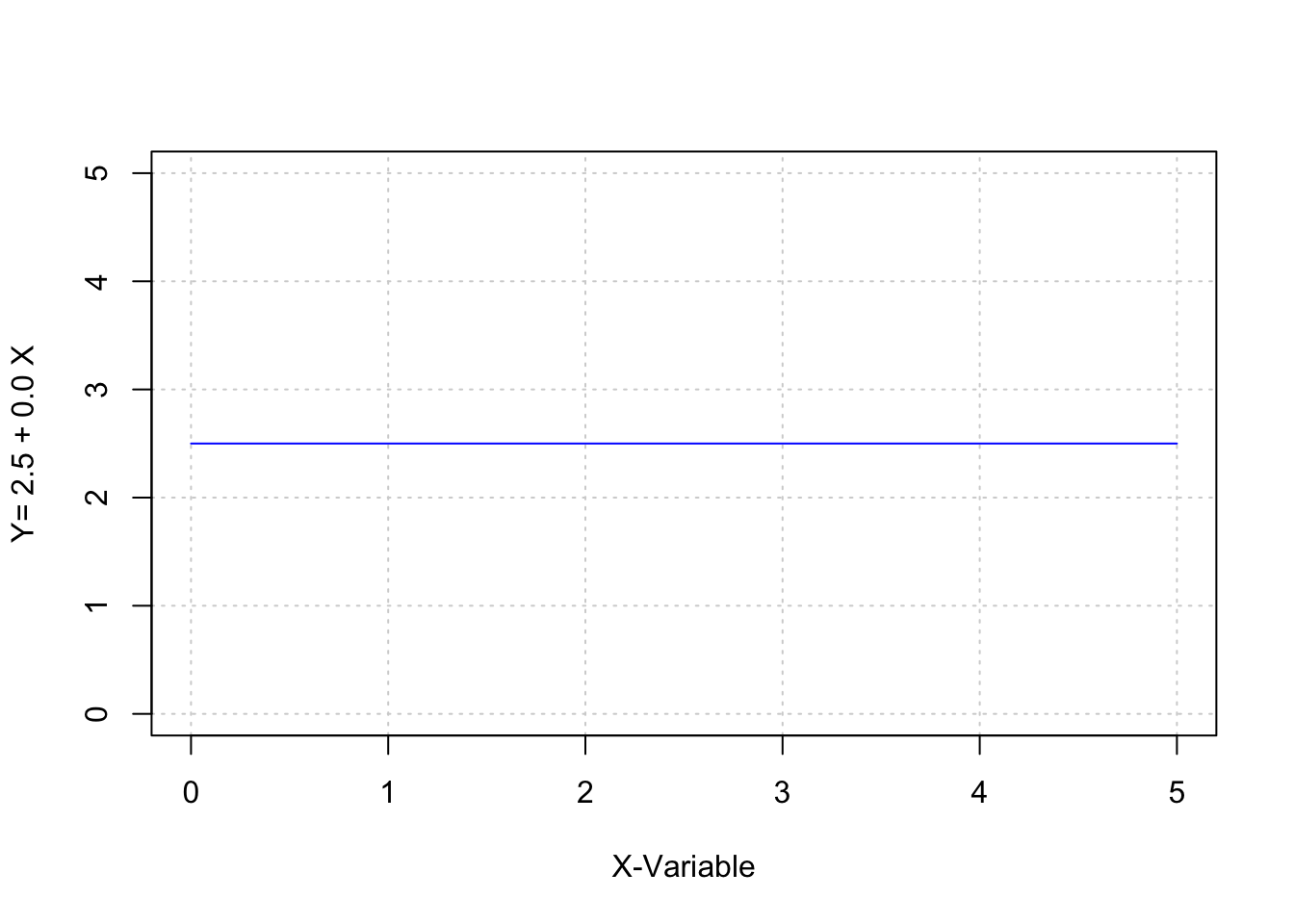
Da solche deterministischen Beziehungen in der Regel nicht der Realität entsprechen, wird die Regressionsgleichung (für die Beziehung zwischen zwei Variablen) um einen stochastischen Fehlerterm erweitert. In der einfachen Regression wird der Parameter \(\varepsilon\) verwendet. Als Residuum bezeichnet, bringt \(\varepsilon\)_ zum Ausdruck, dass die Variable Y neben der systematischen Beziehung zwischen X und Y auch “noch Variationen enthält, die nicht durch Variationen in der Variable X erklärbar sind” (Dolic, 2010, S. 214).
\[ y_i=\alpha +\beta x_i + \varepsilon_i\]
Das Residuum \(\varepsilon_i\) definiert sich als Differenz der prognostizierten (berechneten) und der realen (beobachteten) Werte der abhängigen Variablen:
\[\varepsilon_i= \hat{y_i}-y_i\]
Die Abbildung bildet neben dem deterministischen Zusammenhang, in dem die Variablen X per Definition über die Werte in Y bestimmt, auch einen vorstellbaren stochastischen Zusammenhang ab, indem das deterministische Modell durch einen normalverteilten Fehler erweitert wird.
a <- 0.5
b <- 1.0
x <- 1:9 #Wertebereich für X
y.d <- a+b*x
cbind(x,y.d) ## x y.d
## [1,] 1 1.5
## [2,] 2 2.5
## [3,] 3 3.5
## [4,] 4 4.5
## [5,] 5 5.5
## [6,] 6 6.5
## [7,] 7 7.5
## [8,] 8 8.5
## [9,] 9 9.5plot(x,y.d,type="l",xlim=c(0,10),ylim=c(0,10),
xlab="X-Variable",ylab="Y-Variable",
panel.first=grid(), col="blue")
set.seed(1899)
# Neun normalverteilte Zufallswerte für den Fehler 'e'
e <- rnorm(9)
y.e <- a+b*x+e
cbind(x,y,round(y.e,2),round(e,2))## x y
## [1,] 1 2.5 2.13 0.63
## [2,] 2 2.5 3.27 0.77
## [3,] 3 2.5 4.11 0.61
## [4,] 4 2.5 4.70 0.20
## [5,] 5 2.5 6.13 0.63
## [6,] 6 2.5 5.29 -1.21
## [7,] 7 2.5 9.54 2.04
## [8,] 8 2.5 9.04 0.54
## [9,] 9 2.5 9.75 0.25lines(y.e, type="b")
text(3,5,labels="Y=a+b*X+Fehler")
text(1,1,labels="Y=a+b*X",col="blue")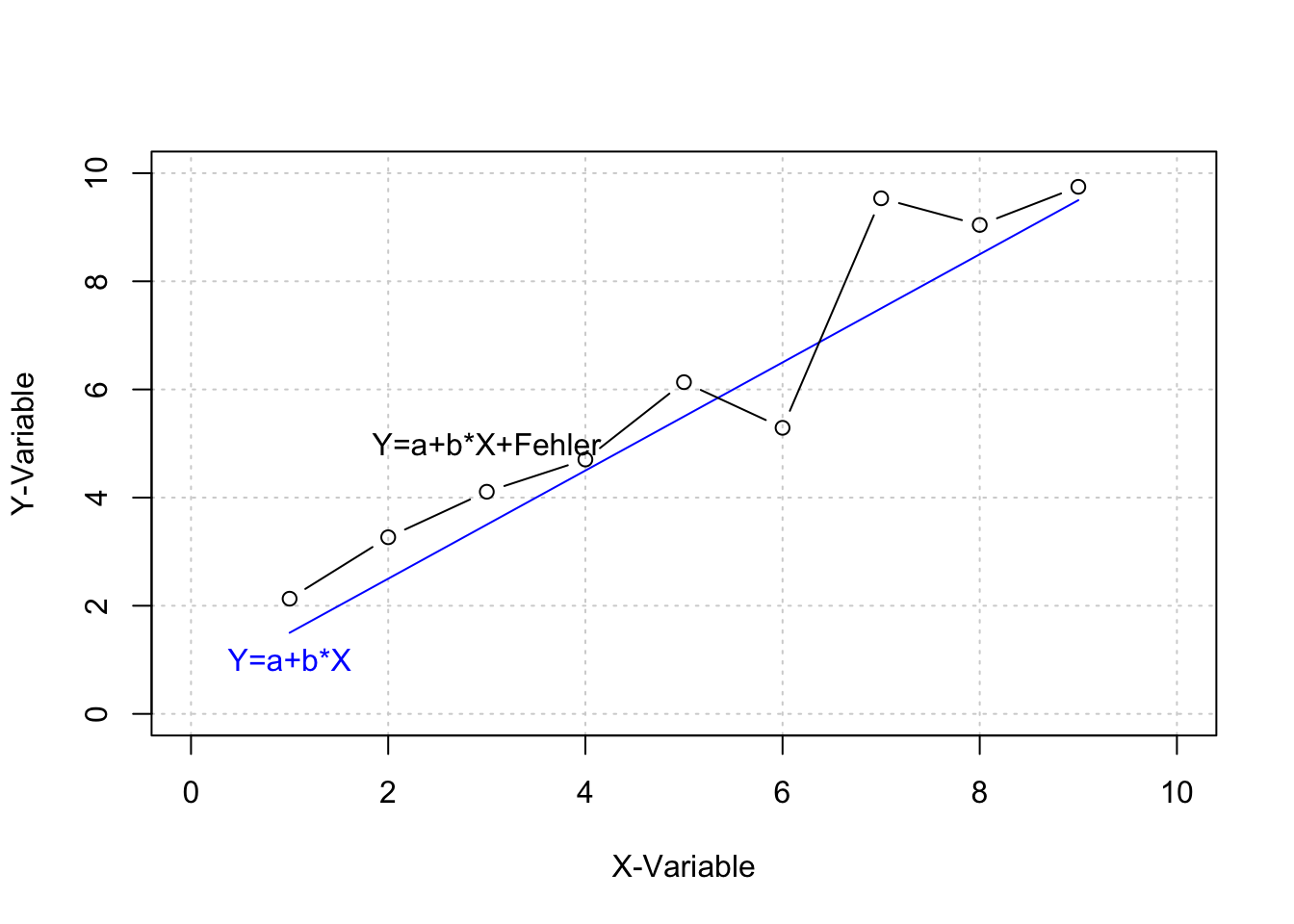
Die typische Forschungspraxis geht aber häufig in umgekehrter Weise vor. Aus vorliegenden Werten für zwei Variablen wird eine lineare Gleichung bestimmt. Dazu möchten die Parameter a und b so gewählt werden, dass die Gleichung alle vorhandenen Variablenpaare möglichst präzise prognostizieren kann.
Die ideale Bestimmung der Parameter a und b liegt dann vor, wenn keine Abweichung zwischen den prognostizierten (berechneten) und den realen (beobachteten) Werten der Variable Y auftreten, d.h. wenn das Residuum \(\varepsilon_i\) für alle geschätzten \(\hat{y_i}\) gleich Null beträgt.
Weil dieses Ideal so unrealistisch wie deterministisch ist, wird nur die optimale Schätzgleichung bestimmt. Nach der Methode der kleinsten Quadrate (OLS), werden a und b so bestimmt, dass die Summe der quadrierten Residuen möglichst minimal wird:
\[\sum_{i=1}^n(\hat{y}-y_i)^2=min!\]
Statistiksoftware wie z.B. Excel, SPSS oder R bestimmen in ihrer Standardeinstellung nach dieser Methode und geben dem Nutzer im Ergebnis die Parameterschätzungen für a und b. Bezogen auf die oben beschriebenen Unterschiede zwischen dem deterministischen Zusammenhang \((y_d)\) und dem stochastischen Zusammenhang \((y_e)\) werden im Folgenden Daten für beide Annahmen generiert. Die dann folgende lineare Regression (lm) bestimmt die Parameter für beide Regressionsmodelle.
# Daten generieren
a <- 0.5
b <- 1.0
x <- 1:9 #Wertebereich für X
# Deterministischer Zusammenhang
y.d <- a+b*x
# Stochastischer Zusammenhang
set.seed(1899)
# Neun normalverteilte Zufallswerte für den Fehler 'e'
e <- rnorm(9)
y.e <- a+b*x+e
cbind(x,y.d,round(y.e,2),round(e,2))## x y.d
## [1,] 1 1.5 2.13 0.63
## [2,] 2 2.5 3.27 0.77
## [3,] 3 3.5 4.11 0.61
## [4,] 4 4.5 4.70 0.20
## [5,] 5 5.5 6.13 0.63
## [6,] 6 6.5 5.29 -1.21
## [7,] 7 7.5 9.54 2.04
## [8,] 8 8.5 9.04 0.54
## [9,] 9 9.5 9.75 0.25Im Fall des deterministischen Zusammenhangs zwischen \(x\) und \(y_d\) wird das lineare Regressionsmodell immer das folgende Ergebnis aufzeigen:
# Regressionsmodell
lm(y.d~x)##
## Call:
## lm(formula = y.d ~ x)
##
## Coefficients:
## (Intercept) x
## 0.5 1.0Die lineare Regression nach der Methode der kleinsten Quadrate ergibt einen Wert von 0.5 für a und einen Wert von 1.0 für b. Damit wurden exakt die Parameter bestimmt, nach denen die Werte generiert wurden.
Für den zweiten Fall (die Regression mit Daten, die einen stochastischen Zusammenhang darstellen sollen) werden abweichende Parameter a und b bestimmt.
# Regressionsmodell
lm(y.e~x) ##
## Call:
## lm(formula = y.e ~ x)
##
## Coefficients:
## (Intercept) x
## 1.0588 0.9873Damit wird nichts anderes aufgezeigt, als dass der in \(y_e\) enthaltene Fehler zu einer abweichenden Bestimmung von a und b führt. Um zu bestimmen, wie stark die Varianz in Y durch X verändert wird, wird eine sogenannte Varianzzerlegung vorgenommen und in Form des Determinationskoeffizienten \(R^2\) (auch Bestimmtheitsmaß genannt) angeboten.
Dieser Wert stellt die durch die Varianz in X erklärbare Varianz von Y in Relation zu der gesamten Varianz von Y. Ein kleiner Determinationskoeffizient (\(R^2\) ≤0.1) zeigt an, dass die Varianz der abhängigen Variable Y nur zu einem sehr geringen Teil (10 Prozent) durch die Varianz der unabhängigen Variablen X erklärt werden kann.
Neben dem Determinationskoeffizienten existieren weitere relevante Parameter der Modell-Statistik. Entscheidend für die Hypothesentestung ist der Steigungskoeffizient b bzw. seine standardisierte Form \(\beta\). Der (unstandardisierte) Steigungskoeffizient kann, je nach Skalenlänge der Variablen, einen Wertebereich von -\(\infty\) < b < +\(\infty\) annehmen. Mit einem negativen Wert für b wäre die inhaltliche Aussage assoziiert, dass größere Werte in X mit kleineren Werten in Y korrespondieren. Umgekehrt werden positive Werte für b mit einem positiven Zusammenhang von X auf Y dargestellt.
Typischerweise soll eine solche Aussage (Hypothese) hinsichtlich ihrer Signifikanz interpretiert werden. Der Parameter b wird dabei in Hinsicht auf die Nullhypothese (b=0) getestet. Aus b und seinem Standardfehler (b) wird die Prüfgröße bestimmt (t-Wert) und der in der t-Verteilung korrespondierende p-Wert ermittelt. Ist der p-Wert ≤ 0.05, wird die Nullhypothese verworfen (siehe auch Hypothesentestung). Ein insignifikanter p-Wert verweist inhaltlich auf die Annahme, dass in der Population b=0 ist.
# Regressionsmodell
model <- lm(y.e~x)
summary (model)##
## Call:
## lm(formula = y.e ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.69237 -0.19696 0.08508 0.13918 1.56501
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.0588 0.6463 1.638 0.145
## x 0.9873 0.1149 8.597 5.74e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8896 on 7 degrees of freedom
## Multiple R-squared: 0.9135, Adjusted R-squared: 0.9011
## F-statistic: 73.9 on 1 and 7 DF, p-value: 5.742e-05In den bisherigen Ausführungen besteht kein Zweifel über die Unterscheidung von unabhängiger und abhängiger Variablen. Die Werte wurden für X spezifiziert und korrespondierende Werte für Y berechnet. Dabei wird die Manipulation der unabhängigen Variablen simuliert, so dass die abhängige Variable (wie in einem experimentellen Forschungsdesign) als Konsequenz der Manipulation von X angesehen werden kann. Wenn nur unzureichende Informationen über die kausale Wirkungsrichtung zwischen Variablen bestehen, muss der Forschende zunächst Aussagen auf Grundlage der Kovarianz der Variablen treffen.
set.seed(1975)
# normalverteilte Zufallswerte für X mit einem Mittelwert von 2.5
x <- 2.5+rnorm (1000)
a <- 0.5
b <- 1
# Deterministischer Zusammenhang
y.d <- a+b*x
# Stochastischer Zusammenhang
e <- rnorm(1000)/2 #normalverteilte Zufallswerte für 'e'
# Stochastischer Zusammenhang
y.e <- a+b*x+e
data <- as.data.frame(cbind(x, y.d, y.e, e))
plot(x,ye,xlim=c(1,5),ylim=c(1,5),
xlab="X-Variable",ylab="Y (stochastisch)",
panel.first=grid(), col="blue")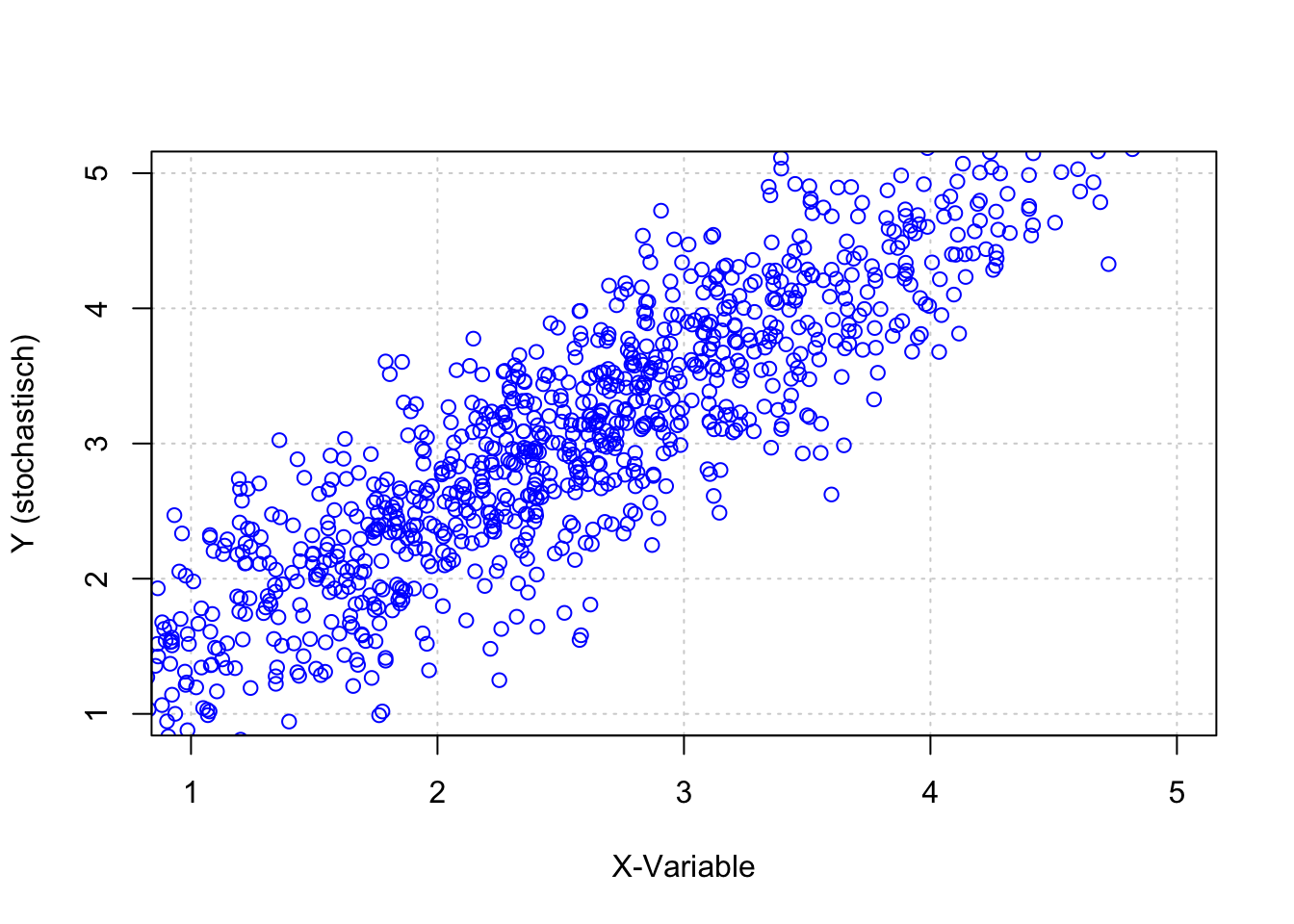
cov(x,y.e)## [1] 1.058476Das Beispiel verdeutlicht, dass zwischen den Variablen \(X\) und \(Y_e\) eine Kovarianz von etwa \(cov(x, y_e)=1.04\) besteht. Inhaltlich bedeutet dies, dass bei einem Wertzuwachs von \(X\) in Höhe von Eins, ein durchschnittlicher Wertzuwachs in \(Y_e\) in Höhe von 1.06 zu erwarten ist. Es lässt ebenso die Aussage zu, dass mit bei einem Wertzuwachs von \(Y_e\) in Höhe von Eins ein durchschnittlicher Wertzuwachs in \(X\) in Höhe von 1.06 zu erwarten ist.
Aus den getroffenen Annahmen wissen wir, dass die Variationen in X als Ausgangspunkt für Variationen in Y angesehen werden können. Daher kann der Zusammenhang auch als Regression aufgefasst werden. Die \(cov(x,y)\) kann als Regression dargestellt werden, indem der Quotient der \(cov(x,y)\) und der Varianz in X, im Folgenden als \(var(x)\) dargestellt, bestimmt wird (Kenny, 2004, S. 23):
\[b_{YX}=\frac{cov(x,y)}{var(x)}\]
Die Varianz von x wird in R bestimmt durch die Anweisung:
var(x)## [1] 1.056424So kann der Regressionskoeffizient b, für die Annahme, dass \(X\) die unabhängige und \(Y_e\) die abhängige Variable ist, bestimmt werden aus:
# Bestimmen des Regressionskoeffizienten b für die Annahme,
# dass X die unabhängige und Ye die abhängige Variable ist.
cov(x, y.e)/ var(x)## [1] 1.001942Damit ist das Ergebnis identisch mit dem Steigungskoeffizienten b aus dem linearen Regressionsmodell.
# Bestimmen von a und b über herkömmliche lineare Regression
lm (y.e~x)##
## Call:
## lm(formula = y.e ~ x)
##
## Coefficients:
## (Intercept) x
## 0.5027 1.0019Zusammenfassend gibt diese Darstellung einen groben Überblick auf die traditionelle Funktionsweise der einfachen linearen Regression. Bei der Ableitung der Fehlerfunktion zur Minimierung der Residuen hatte ich die mathematische Herleitung nicht konsequent zu Ende weiterverfolgt.
Weil dieser Punkt für weitere Betrachtungen wichtig werden kann, sei hier noch einmal darauf eingegangen. Die Summe der quadrierten Fehler ist also gleich den quadrierten Residuen, die als Differenz der mittels Regressionsgleichung geschätzten \(\hat{y_i}\) und der (wahren) Werte \(y_i\) definiert sind.
\[\sum_{i=1}^{n}(\hat{y_i}-y_i)^2 = \sum_{i=1}^{n}((\alpha+\beta x_i)-y_i)^2=min!\]
Gesucht wird hier also eine Funktion für die Parameter \(f(\alpha,\beta)\). Diese kann mathematisch bestimmt werden, indem das im Gleichungssystem aufgelöst wird, nach \(\alpha\) und \(\beta\) umgestellt und die Ableitungen gleich Null gesetzt werden.
Die Existenz eines lokalen Extremwertes wird dann durch die Bildung der ersten und zweiten Ableitung geprüft. Im Resultat ergibt sich: \(\alpha=\overline{y}-\beta \: \overline{x}\) und nach zahlreichen weiteren Umformungen:
\[ \beta= \frac {\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^{n}(x_i-\overline{x})^2}= \frac{cov(x,y)}{var(x)}\]
Eine ausführlichere Herleitung zeigt beispielsweise Dolic (2010, S. 216–217).