Kapitel 6 Anwendungen
Die bisherigen Ausführungen sollten erkennbar machen, dass unterschiedliche Sichtweisen auf kausales Schließen (causal inference) existieren. Pearl & Mackenzie (2018) unterscheidet drei Ebenen kausalen Schließens:
das Assoziieren (association) bezieht sich auf die Beschreibung von Zusammenhängen zwischen Variablen,
die Intervention (intervention) zeigt auf, wie sich die Manipulation einer Variable auf eine andere Variable auswirken kann und
Kontrafaktuale (counterfactuals) bietet die Imagination, was wäre, wenn eine Variable (z.B. ein Ereignis) einen anderen Wert (z.B. eine andere Entscheidung) angenommen hätte (Lübke, Gehrke, Horst & Szepannek, 2020).
Im Folgenden werden zwei zentrale Konzepte multivariater Analyse, die Mediation und die Moderation, vorgestellt. Um die Konzepte zu veranschaulichen, werden hier simulierte Daten genutzt. Im realen Forschungsprozess werden etablierte Skalen verwendet.
6.1 Mediation
Eine verbreitete Definition für die Mediation stammt von Baron & Kenny (1986, S. 1176): „[Mediators are] entities or processes that intervene between input and output.“
So könnte z.B. angenommen werden, dass Lernen zu Wissen führt und Wissen zu Verständnis beiträgt. Der Zusammenhang zwischen Lernen und Verständnis wird demnach durch Wissen mediiert. Die Ergebnisse dieses Modelles wären dahingehend zu interpretieren, dass eine Ursache von Verständnis im Effekt von Wissen besteht. Wissen selbst wird durch Lernen verursacht.
#Erstellen von Simulationsdaten für Mediation
set.seed(1896)
n <- 1000 # Festlegung der Größe des Samples
# normalverteilte Zufallswerte für Lernen werden bestimmt
learning <- rnorm(n)
# Wissen wird aus Lernen bestimmt
knowing <- 5 * learning + rnorm(n)
# Verständnis wird aus Wissen bestimmt
understanding <- 3 * knowing + rnorm(n)
plot (learning, understanding)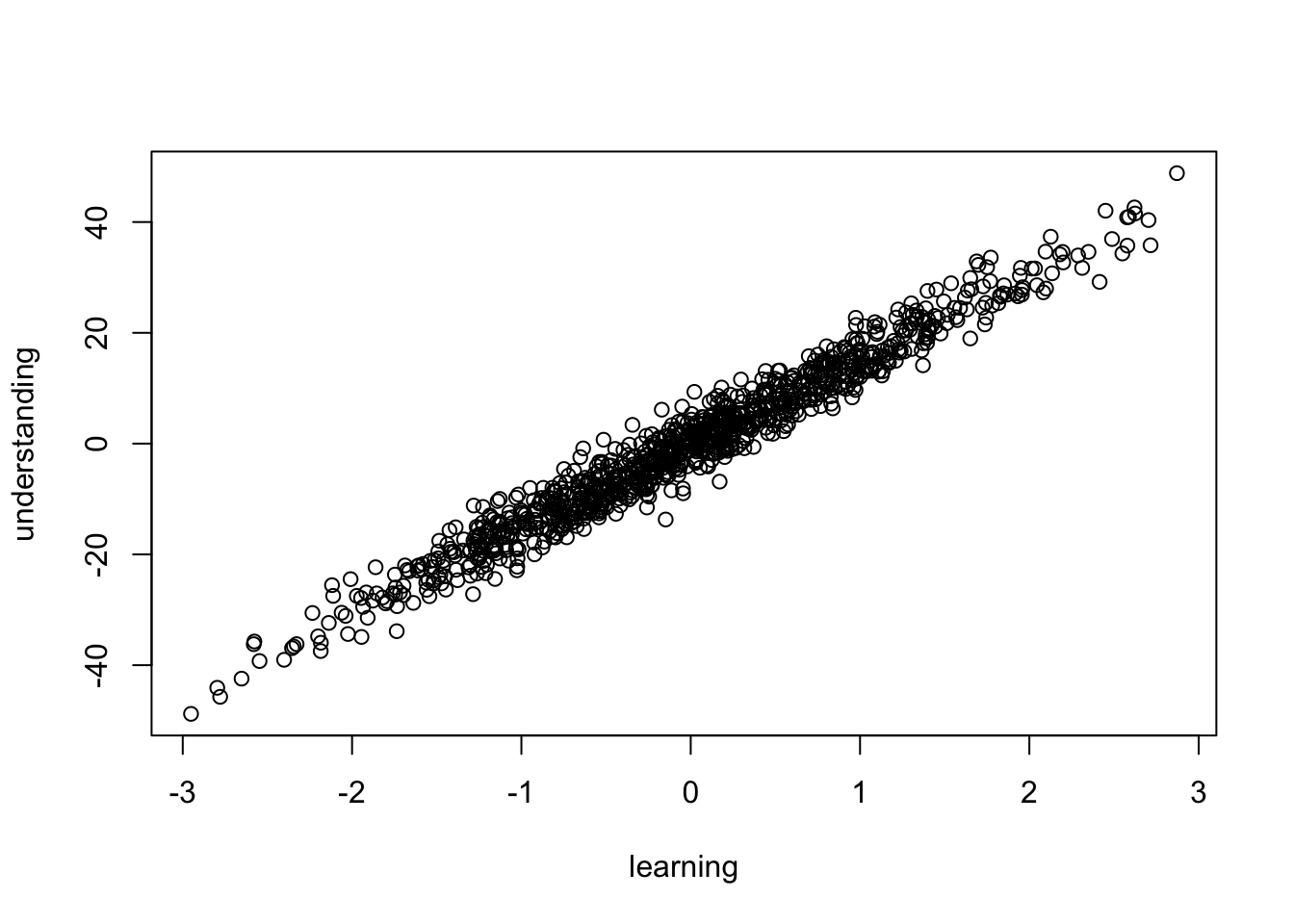
Baron & Kenny (1986, S. 1177) schlagen einen analytischen Test vor, mit dem ein Mediator getestet werden kann. Hierfür werden nacheinander drei Regressionsmodelle überprüft. Die Grundvoraussetzung ist, dass ein signifikanter Zusammenhang zwischen Lernen und Verständnis existiert.
In den generierten Daten wird dieser Grundzusammenhang durch einen signifikanten Regressionskoeffizienten (\(\beta\)=15.12, t=154.59, p≤0.001) unterstützt .
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Grundzusammenhang
summary(lm (understanding ~ learning))##
## Call:
## lm(formula = understanding ~ learning)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.442 -2.136 -0.123 2.125 9.039
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.02228 0.09661 -0.231 0.818
## learning 15.12088 0.09782 154.585 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.054 on 998 degrees of freedom
## Multiple R-squared: 0.9599, Adjusted R-squared: 0.9599
## F-statistic: 2.39e+04 on 1 and 998 DF, p-value: < 2.2e-16Im ersten Analysemodell wird der Regressionskoeffizient für die Regression der unabhängigen Variablen (in unserem Fall Lernen) auf den Mediator (in unserem Fall Wissen) bestimmt.
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Erster Schritt
summary (lm (knowing ~ learning))##
## Call:
## lm(formula = knowing ~ learning)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.85145 -0.68160 -0.07698 0.69096 2.97009
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.005812 0.030715 -0.189 0.85
## learning 5.030412 0.031098 161.758 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.971 on 998 degrees of freedom
## Multiple R-squared: 0.9633, Adjusted R-squared: 0.9632
## F-statistic: 2.617e+04 on 1 and 998 DF, p-value: < 2.2e-16Im zweiten Schritt wird der Koeffizient des potenziellen Mediators (in unserem Fall Wissen) auf die abhängige Variable (in unserem Fall Verständnis) bestimmt und im letzten Schritt wird das multivariate Regressionsmodell (der unabhängigen Variablen und des Mediators auf die abhängige Variablen) bestimmt.
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Zweiter Schritt
summary (lm (understanding ~ knowing))##
## Call:
## lm(formula = understanding ~ knowing)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.15858 -0.62152 -0.01226 0.65263 3.10540
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.004929 0.030765 -0.16 0.873
## knowing 3.005005 0.006077 494.48 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9725 on 998 degrees of freedom
## Multiple R-squared: 0.9959, Adjusted R-squared: 0.9959
## F-statistic: 2.445e+05 on 1 and 998 DF, p-value: < 2.2e-16Damit der Mediator angenommen werden kann, sollte aus den Modelle 1 und 2 signifikante Regressionskoeffizienten hervorgehen und in Modell 3 sollte der Regressionskoeffizient des Mediators signifikant und der der unabhängigen Variablen insignifikant sein.
# Three-steps-mediation-analysis (Baron & Kenny 1986)
# Dritter Schritt
summary (lm (understanding ~ learning + knowing))##
## Call:
## lm(formula = understanding ~ learning + knowing)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.13323 -0.63096 -0.00681 0.65456 3.07422
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.004948 0.030772 -0.161 0.872
## learning 0.121515 0.162537 0.748 0.455
## knowing 2.981736 0.031712 94.026 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9727 on 997 degrees of freedom
## Multiple R-squared: 0.9959, Adjusted R-squared: 0.9959
## F-statistic: 1.222e+05 on 2 and 997 DF, p-value: < 2.2e-16Eine Ausnahme bietet der Fall, dass der Regressionskoeffizient der unabhängigen Variablen zwar noch signifikant, aber deutlich geringer ausfällt. In diesem Fall spricht man von einem partiellen Mediator. Weitere Überprüfungen (Sobel-Test) können hier Klarheit verschaffen.
Das obrige Beispiel beschreibt einen signifikant positiven Zusammenhang zwischen Lernen und Verständnis (\(\beta\)=15.12, t=154.59, p≤0.001)). Untersucht werden soll, ob Wissen ein Mediator für den Zusammenhang zwischen Lernen und Verständnis darstellt.
Der erste Schritt der Mediationsanalyse nach Baron & Kenny (1986) zeigt einen signifikant positiven Zusammenhang zwischen Lernen und Wissen auf (\(\beta\)=5.03, t=161.76, p≤0.001).
Der zweite Schritt der Mediationsanalyse zeigt einen signifikanten positiven Zusammenhang zwischen Wissen und Verständnis auf (\(\beta\)=3.01, t=494.48, p≤0.001).
Im dritten Schritt (der multiplen Regression) ist der Zusammenhang zwischen Lernen und Verständnis unsignifikant (\(\beta\)=0.12, t=0.75, p=0.455) und es wird ein signifikant positiver Zusammenhang zwischen Wissen und Verständnis (\(\beta\)=2.98, t=94.03, p≤0.001) aufgezeigt.
Im Verständnis von Baron & Kenny (1986) kann Wissen damit als Mediator für den Zusammenhang zwischen Lernen und Verständnis angesehen werden.
Das Konzept der Mediation, in der Notation der konditionalen Unabhängigkeit als ‘chain’ bezeichnet, findet sich auch in anderen Analyseverfahren (z.B. Strukturgleichungsmodellierung) wieder. Dabei wird häufig die Unterscheidung zwischen totalen, direkten und indirekten Effekten gemacht (Kline, 2015; Muthén & Asparouhov, 2015).
Der totale Effekt einer unabhängigen Variablen auf die abhängige Variablen ist dabei die Summe des direkten Effektes und dem totalen indirekten Effekt (Muthén, 2011):
\[ TE = DE + TIE \] Der totale indirekte Effekt einer unabhängigen Variable auf eine abhängige Variable ergibt sich aus dem Produkt der Koeffizienten aus dem Regressionsmodell der unabhängigen Variablen (X) auf den Mediator (M) und dem Regressionsmodell des Mediators (M) auf die abhängige Variable (Y).
\[ TIE = \gamma_{X|M} \cdot \beta_{M|Y}\] Für das obige Beispiel ergibt sich somit der indirekter Effekt (TIE) von Lernen auf Verständnis aus dem Produkt der Koeffizienten aus Modell 1 und Modell 3 als: \[5.03 \cdot 2.98 = 14.99\]
Bei einem direkten Effekt in Höhe von 0.12 (Modell 3) ergibt sich ein totaler Effekt von:
\[14.99 + 0.12 = 15.11\]
für den Zusammenhang zwischen Lernen und Verständnis. Dies entspricht in etwa dem Koeffizienten aus Modell 2.
Der indirekte Effekt mach somit etwa 99.2 Prozent des totalen Effektes von Lernen auf Verständnis aus. Mit anderen Worten wird der Zusammenhang zwischen Lernen und Verständnis in diesem Mediationsmodell zu etwa 99 Prozent durch Wissen erklärt.
6.2 Moderation
Eine verbreitete Definition für Moderation stammt von Baron & Kenny (1986, S. 1174):
„In general terms, a moderator is a […] variable that effects the direction and/ or strenght of the relation between an independent or predictor variable and a dependent or criterion variable“.
Es handelt sich hier also nicht um den Effekt einer Ursache (effect of cause) sondern vielmehr um die Ursache eines Effektes (cause of effect). Für metrische Variablen schlagen sie einen analytischen Test vor, der den Produktterm der unabhängigen Variablen und des Moderators einbezieht.
Da analytisch nicht zwischen unabhängiger Variable und Moderator zu unterscheiden ist und die Zuweisung von unabhängiger Variable bzw. Moderator rein theoretisch herzuleiten ist (Baron & Kenny, 1986), wird die Moderationsanalyse häufig auch als Interaktionsanalyse bezeichnet (Berry, Golder & Milton, 2012).
Verschiedene Aspekte sprechen dafür, dass die Werte der interagierenden Variablen vor der Bildung des Produktterms standardisiert oder zumindest zentriert werden (Dawson, 2014). Besondere Beachtung sollte auf hohe Korrelationen zwischen der interagierenden Variablen gerichtet werden. Bei Korrelationen zwischen 0.3 und 0.5 wird von Dawson (2014) die zusätzliche Einbeziehung quadratischer Terme empfohlen, bei Korrelationen >0.5 sollten sie nicht unberücksichtigt bleiben (Dawson, 2014).
Die Bildung quadratischer Terme (nichtlineare Terme) erfolgt durch quadrieren der Werte einer Variablen. In Erweiterung zu diesem Vorgehen können auch Mehrfachinteraktionen (z. B. Interaktionen zwischen drei Variablen) operationalisiert werden Dawson & Richter (2006)].
Die folgende Abbildung von Muthén & Asparouhov (2015) zeigt schematisch ein Mediationsmodell, bei dem zusätzlich eine Interaktion der unabhängigen Variablen und dem Mediator besteht.
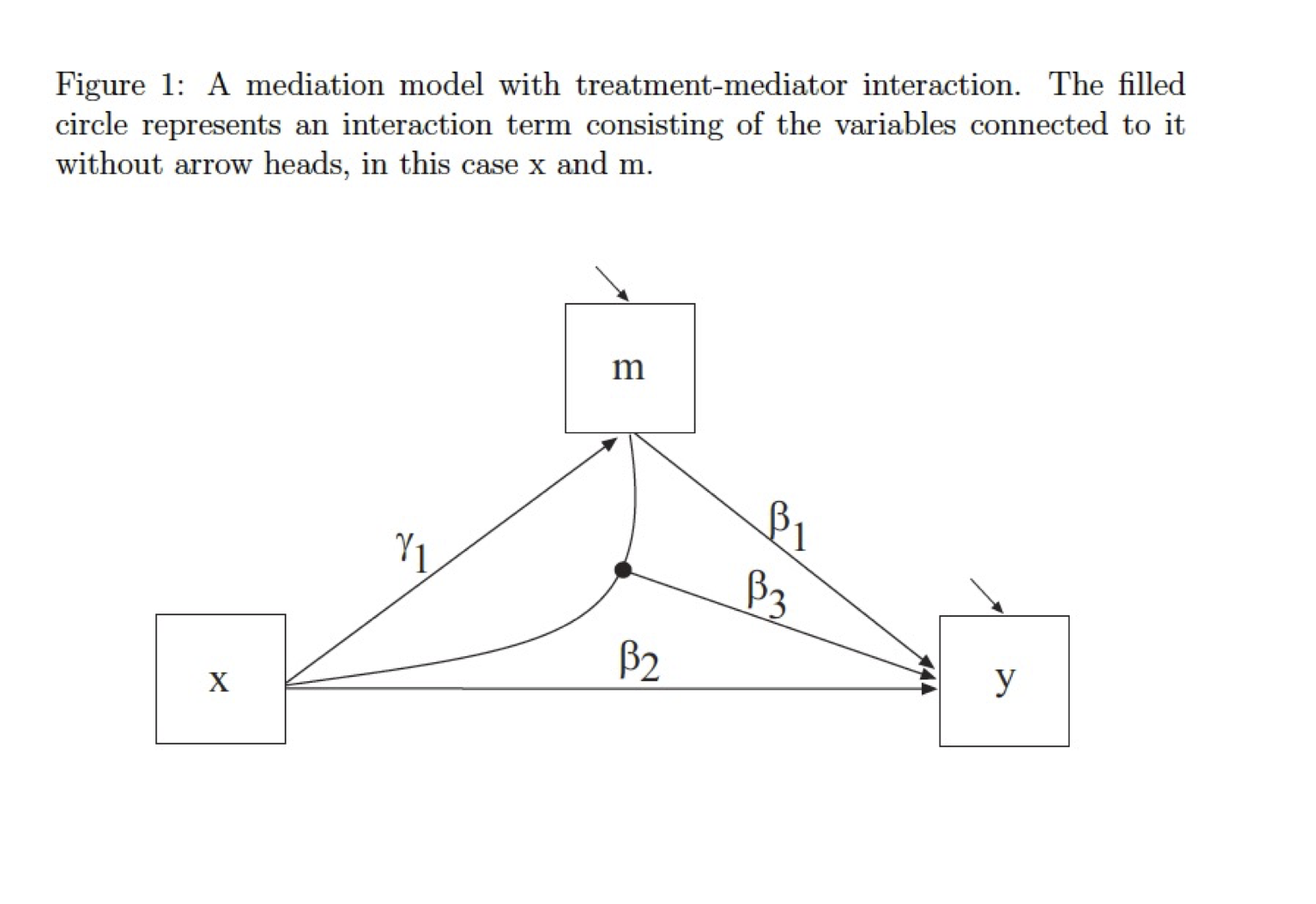
Die resultierende Gleichung lässt sich darstellen als:
\[ y_i=\beta_0 + \beta_1 m_i + \beta_2 x_i + \beta_3 x_i m_i + \varepsilon_{1i} \] \[ wobei: \: m_i=\gamma_0 + \gamma_1 x_i + \varepsilon_{2i}\] Die Simulation wird an dieser Stelle durch die Variable Wissensvertiefung (elaboration) erweitert.
Wir wissen, dass die Vertiefung von Wissen zum Verständnis beiträgt. Zusätzlich wird determiniert, dass die Wissensvertiefung den Zusammenhang zwischen Wissen und Verständnis verstärkt.
#Erstellen von Simulationsdaten für Moderation
set.seed(1896)
n <- 1000 # Festlegung der Größe des Samples
# normalverteilte Zufallswerte für Lernen werden bestimmt
learning <- rnorm(n)
# Wissen wird aus Lernen bestimmt
knowing <- 5 * learning + rnorm(n)
# Wissensvertiefung ist unabhängig vom Wissen
elaboration <- rnorm(n)
# Verständnis wird aus Wissen, Wissensvertiefung und der
# Interaktion aus Wissen und Wissensvertiefung gebildet
understanding <- 3 * knowing + 2*elaboration +
(1.5 * knowing * elaboration) + rnorm(n)
head(cbind(learning, knowing, understanding))## learning knowing understanding
## [1,] 2.03365024 10.993847506 8.4511492
## [2,] 0.13466066 -0.151545780 -0.7177007
## [3,] 0.59787859 3.779447005 14.4147141
## [4,] 0.06392520 0.002531287 0.4289047
## [5,] 0.21673542 2.587983621 1.7939653
## [6,] 0.03408985 0.476003332 -0.9855957Verständnis (understanding) wird demnach durch Wissen (knowing), Wissensvertiefung (elaboration) und die Interaktion von Wissen mit Wissensvertiefung determiniert. Zusätzlich trägt ein normalverteilter zufälliger ‘Fehler’ zum Verständnis bei.
Die folgende Abbildung stellt die drei bivariaten Zusammenhänge zwischen den Variablen dar.
par(mfrow=c(1,3))
plot (knowing, understanding)
plot (knowing, elaboration)
plot (elaboration, understanding)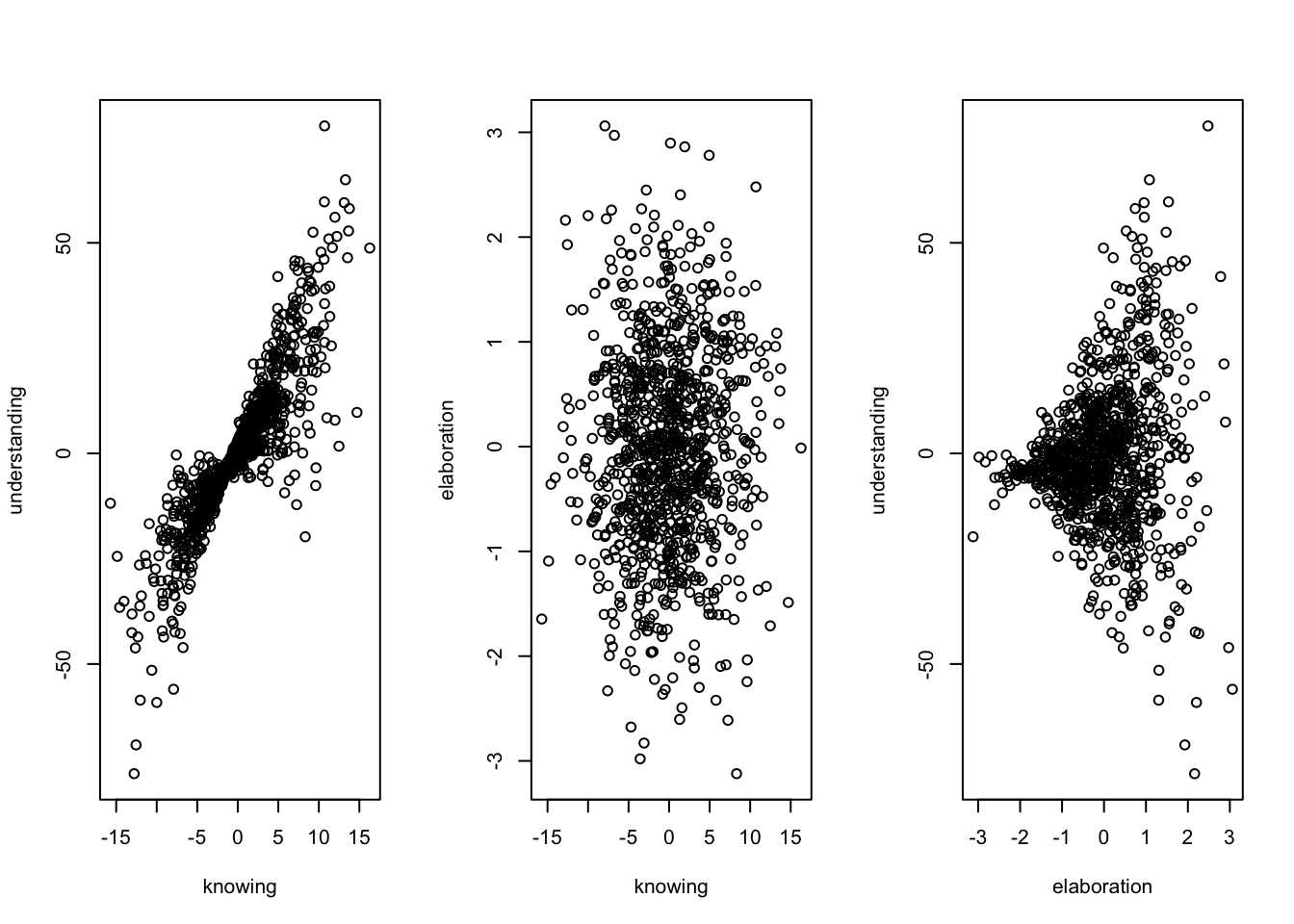
Zwischen Wissen und Verständnis (links) liegt scheinbar ein positiver linearer Zusammenhang vor.
Der Zusammenhang zwischen Wissen und Wissensvertiefung (mitte) stellt sich unsystematisch dar.
Der Zusammenhang zwischen Wissensvertiefung und Verständnis (rechts) weist auf eine zunehmende (scheinbar unsystematische) Streuung von Verständnis bei zunehmender Wissensvertiefung hin.
Die Kombination der drei Plots bietet ein erweitertes Verständnis im dreidimensionalen Raum, bietet jedoch keine deutlichen Vorteile in der Repräsentation.
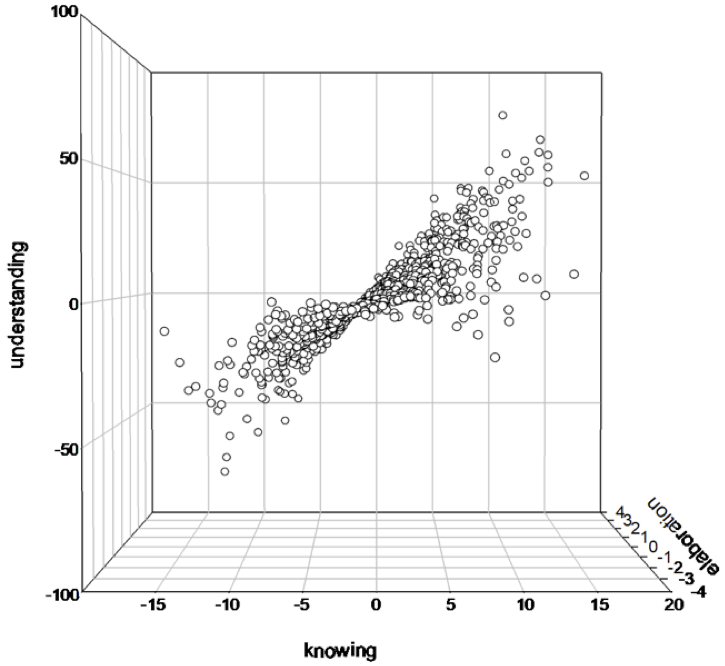
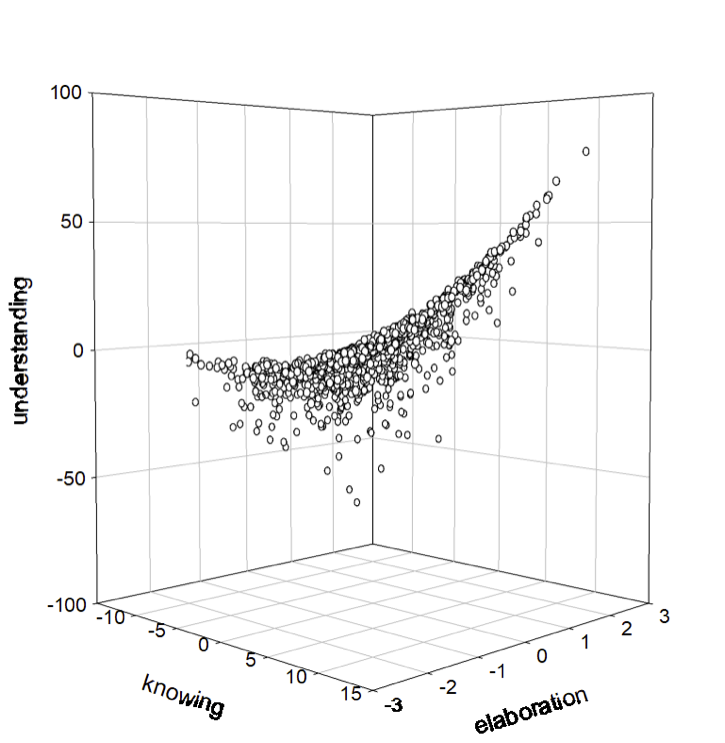
Eine Möglichkeit bietet der zweidimensionale Plot mit Farbzuweisung durch die Ausprägung der Variable Wissensvertiefung. An dieser Stelle wird die R-Programm-Bibliothek ‘ggplot2’ (Wickham, 2016) eingesetzt.
# Visualisierung der Daten mit ggplot2
# Zusammenfassen der drei Variablen in einem Datenframe
data <-data.frame(cbind(knowing, elaboration, understanding))
library(ggplot2)
ggplot (data, aes(x=knowing, y=understanding)) +
geom_point(aes(color= elaboration))+ theme_minimal()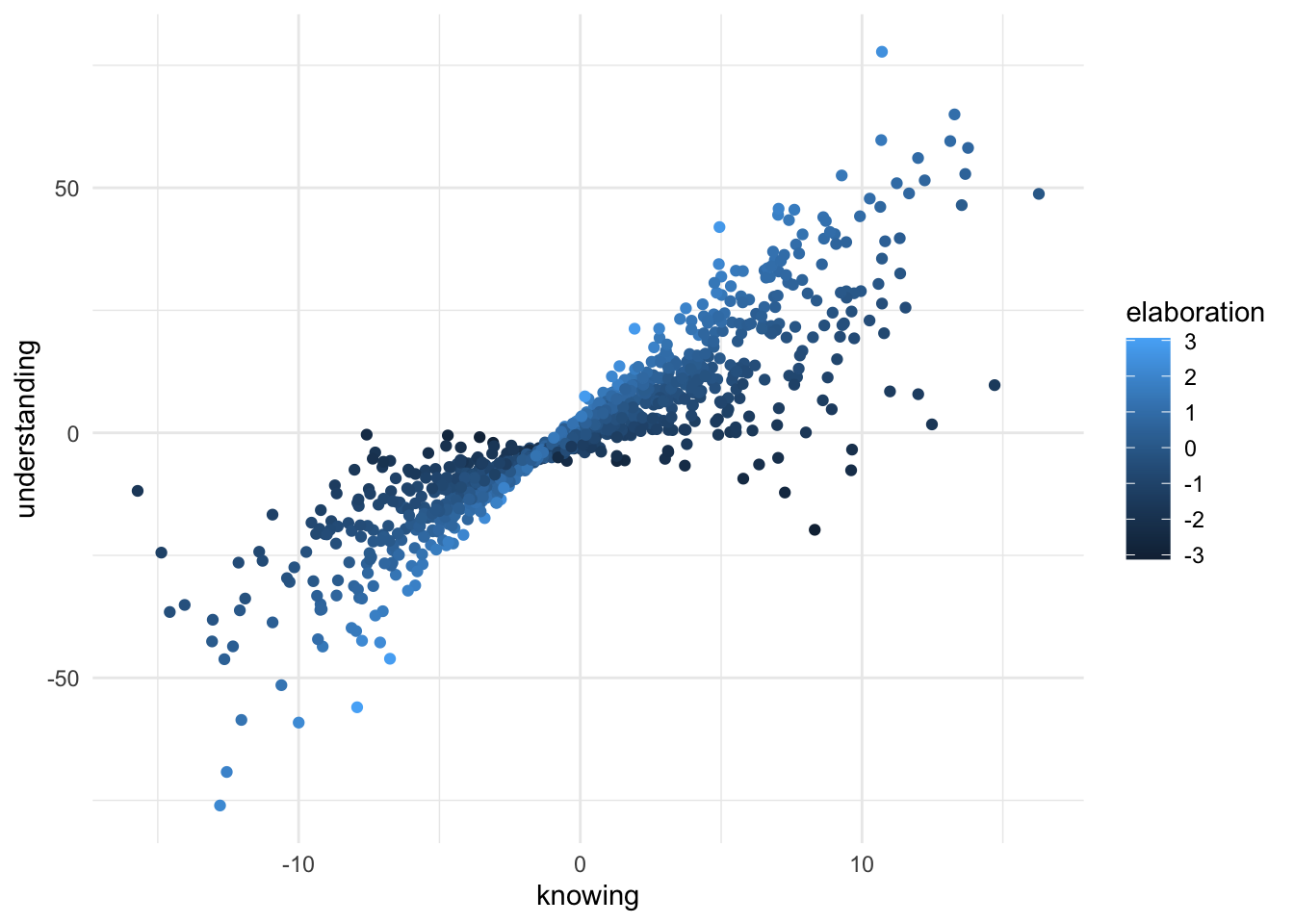
# Kontrastrieren von Wissensvertiefung in hoch vs. gering
# Werte in Wissensvertiefung >= 0 werden mit 1 kodiert; Werte < 0 mit 0
#data$hi_elab <- ifelse (data$elaboration>=0,1,0)
#ggplot (data, aes(x=knowing, y=understanding))+ geom_point(aes(color= hi_elab))+ theme_minimal()Es wird deutlicher, dass bei geringem Wissen (links) die dunkelblau gefärbten Datenpunkte (welche eine geringe Wissensvertiefung repräsentieren) mit höheren Werten von Verständnis einhergehen als die helblau eingefärbten Datenpunkte (welche eine hohe Wissensvertiefung repräsentieren). Mit zunehmendem Wissen (rechts) gehen die hellblau gefärbten Datenpunkte jedoch mit deutlich höheren Werten im Verständnis einher, während die dunkelblau gefärbten Datenpunkte nur mit einem geringen Zuwachs im Verständnis einhergehen.
Das Ergebnis des linearen Regressionsmodelles mit Interaktionsterm weist drei höchst signifikante Regressionskoeffizienten auf. Mit \(\beta\)=2.99 (t=487.40, p≤0.001) wird ein signifikant positiver Zusammenhang zwischen Wissen und Verständnis dargestellt. Auch die Wissensvertiefung weist auf einen signifikant positiven Zusammenhang zum Verständnis hin (\(\beta\)=1.76, t=54.90, p≤0.001). Der signifikante Interaktionsterm unterstützt die Annahme einer Interaktion zwischen Wissen und Wissensvertiefung auf das Verständnis (\(\beta\)=1.51, t=247.86, p≤0.001).
Typischerweise werden die Ergebnisse von Interaktionsanalysen in Zweifach-Interaktions-Plots stark vereinfacht dargestellt und kontrastieren dann die (geschätzen) Werte der abhängigen Variablen an den Rändern der Werte der interagierenden Variablen.
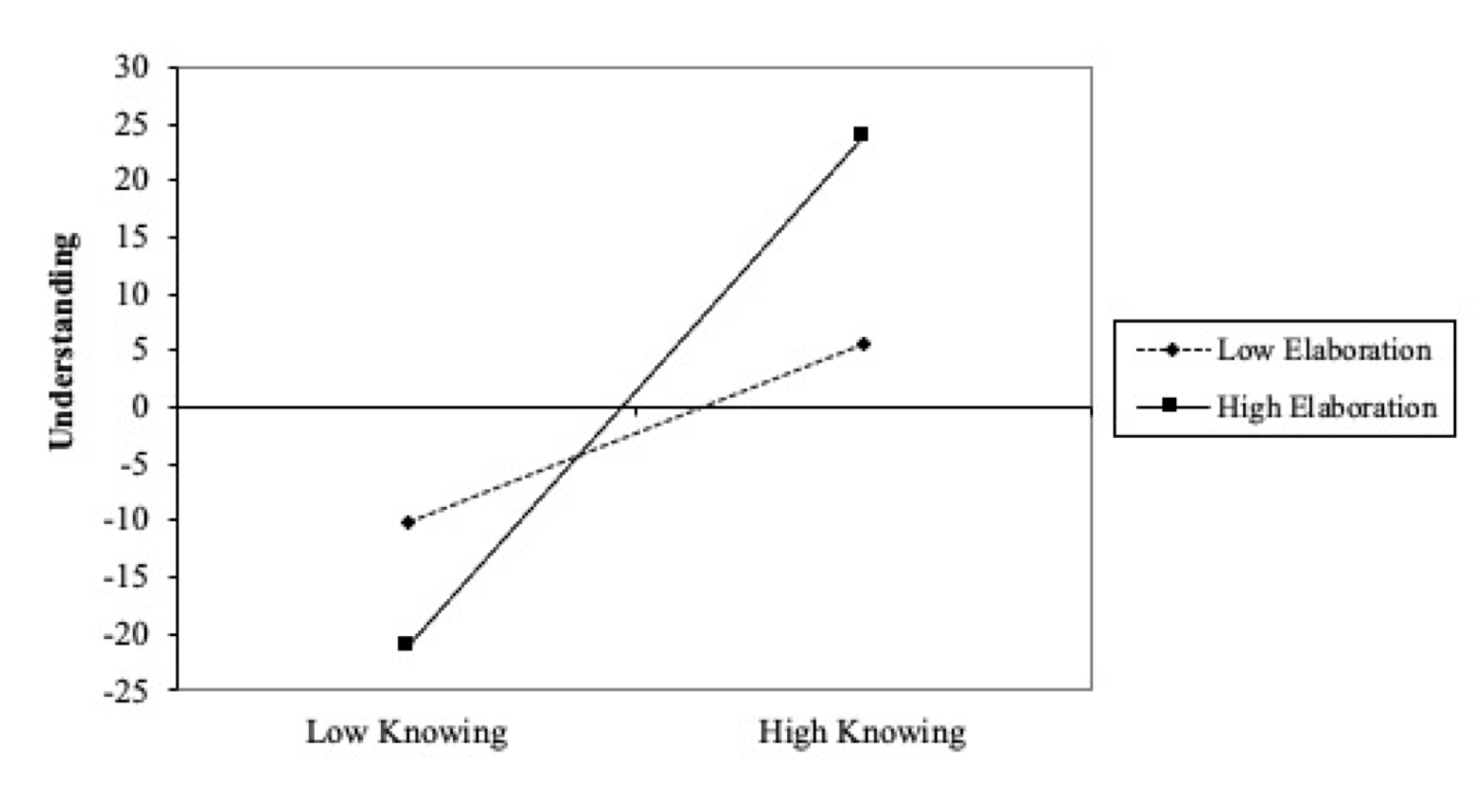
Die Regressionsgeraden weisen darauf hin, dass das Interaktionsmodell das Verständnis in ähnlicher Weise prognostiziert, wie es in den Daten vorgefunden wurde. Bei geringem Wissen wird deutlich, dass hohe Wissensvertiefung mit keinen Vorteil für das Verständnis bietet. Mit steigendem Wissen wird der fördernde Einfluss der Wissensvertiefung deutlicher und überwiegt mit höherem Verständnis bei hohem Wissen.
Als alternative Visualisierungformen bieten sich Konturenlinien oder farbliche Konturenplots an, welche unterschiedliche Bereiche von Wissen und Wissensvertiefung hervorheben, in denen hohe Werte für das Verständnis (rote Bereiche) bzw. geringe Werte für das Verständnis (blaue Bereiche) überwiegen.
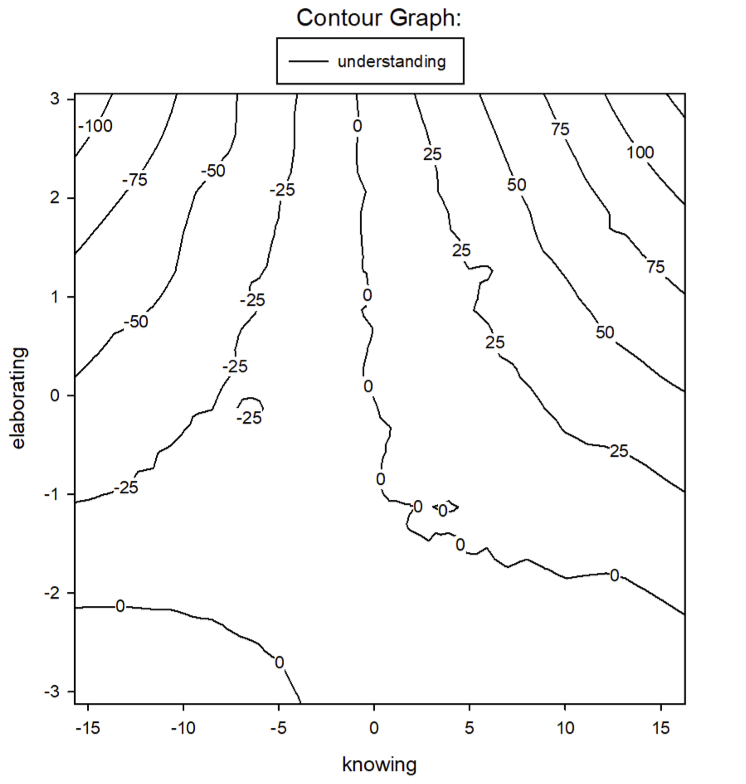
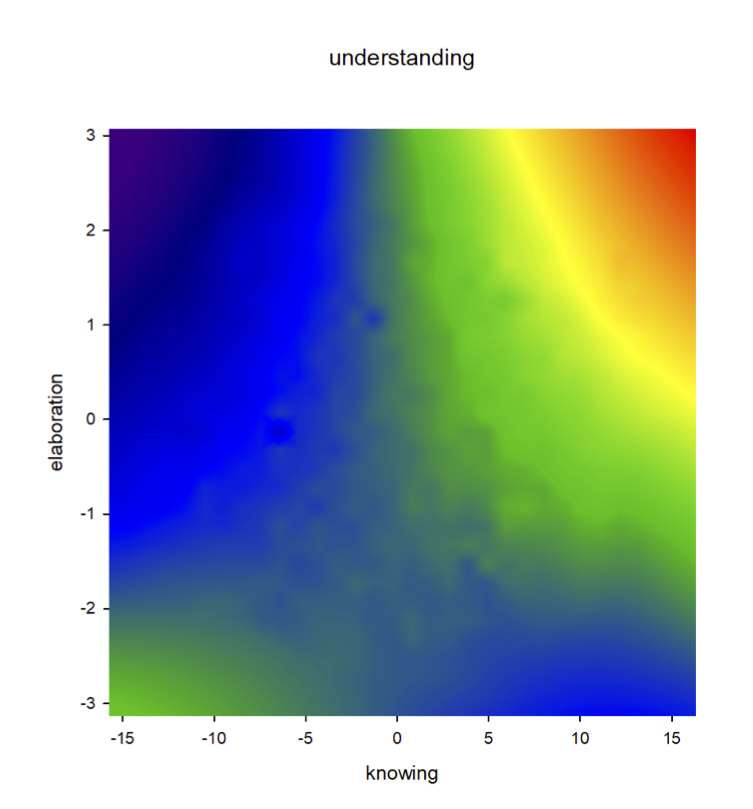
Hierbei handelt es sich um die Darstellung der tatsächlichen Daten und nicht um die geschätzten Werte aus dem Regressionsmodell.
6.3 Unkorreliert versus Unabhängig
An dieser Stelle soll noch einmal die Unterscheidung zwischen Beziehungslosigkeit und Unabhängig hervorgehoben werden. Sind sind zwei variablen X und Y unkorreliert, wenn der Korrelationskoeffizient dieses Variablenpaares Null beträgt.
An verschiedenen Zeitpunkten dieses Kurses wurde bereits darauf hingewiesen, dass dieser Korrelationskoeffizient durch die An- oder Abwesenheit weiterer Variablen unterschiedliche Werte annehmen kann. Bereits 1899 haben Pearson, Lee & Bramley-Moore (1899) darauf hingewiesen, dass Korrelationen durchaus konstruiert werden können:
“To those who persist on looking upon all correlation as cause and effect, the fact that correlation can be produced between two quite uncorrelated characters A and B by taking an artificial mixture of the two closely allied races, must come as rather a shock.” (Pearson et al., 1899, S. 278)
Die Aussage ist dementsprechend, dass wenn der Korrelationskoeffizient eines Variablenpaares (X,Y) ungleich Null ist, dann korrelieren die Variablen X und Y.
Dem gegenüber sind zwei Variablen unabhängig voneinander, wenn ihre gemeinsame Wahrscheinlichkeitsfunktion für alle x und y das Produkt ihrer marginalen Wahrscheinlichkeitsfunktionen P ist.
\[ P_{X,Y}(x,y) = P_X(x) \cdot P_Y(y)\] 1. Wenn X und Y nicht unabhängig sind, dann sind sie abhängig. (Wenn zum Beispiel die Variable Y eine Funktion von X ist, dann sind X und Y immer abhängig.)
Wenn X und Y unabhängig sind, dann sind die ebenfalls unkorreliert.
Wenn X und Y unkorreliert sind, dann sind sie im Allgemeinen nicht unabhängig.
Der einzige allgemeine Fall, wenn das Fehlen von Korrelation auf Unabhängigkeit schließen lässt, ist gegeben, wenn die gemeinsame Verteilung von X und Y eine Gaußsche Verteilung (Normalverteilung) aufweist.
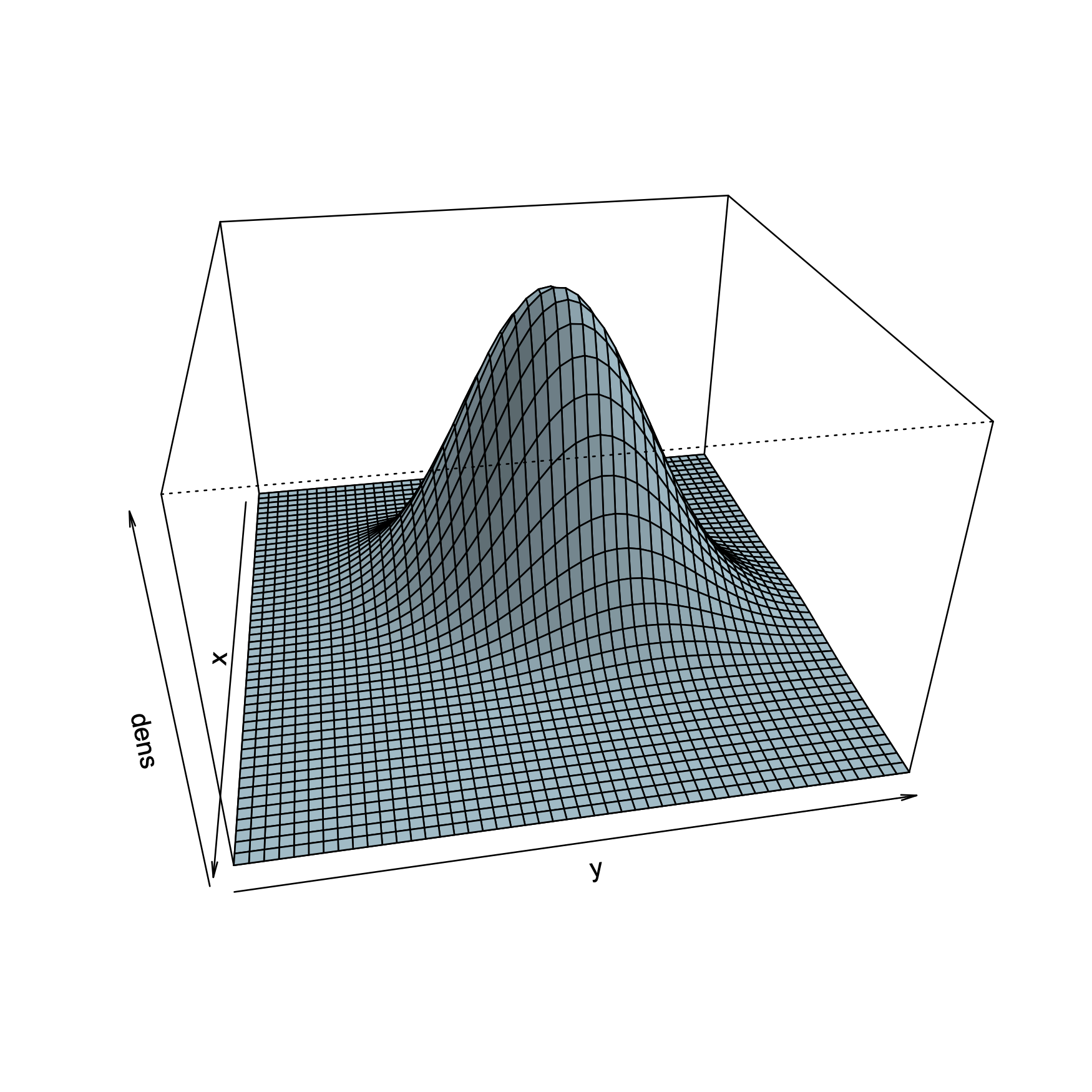
Dieser vierte Punkt bezieht sich auf das Konzept der Multivariaten Normalverteilung. Werden die Häufigkeitsverteilungen zweier Variablen auf die Achsen eines Koordinatensystems übertragen, sollte daraus eine dreidimensionale Glockenkurve resultieren, was jedoch in der Realität nahezu nie vorzufinden ist.