Chapter 2 Einleitung
Aussagen werden in den Sprach- und Kognitionswissenschaften als Propositionen bezeichnet und bilden die kleinstmöglichen Wissenseinheiten ab, die entweder wahr oder falsch sein können (Westermann, 2000, S. 69).
Betrachten wir die Bedingung (x) und das Ergebnis (y) als Propositionen, können sie wahr oder falsch sein.
Werden Aussagen in logischer Weise verknüpft, lassen sich anhand von Schlussregeln, die in der deduktiven Logik gelten, “Folgerungen mit Gewissheit aus den Prämissen ableiten” (Anderson, 1996, S. 304).
Die Propositionen X und Y können logisch auf unterschiedlicher Weise verknüpft werden und bilden dann eine zusammengesetzte Aussage in Form einer Behauptung. Eine mögliche bedingte Aussage wäre: “Wenn X wahr ist, dann ist Y wahr”, formal ausgedrückt als:
\[X \to Y\] Der Pfeil von X nach Y wird als Implikation stellt ebenfalls eine Proposition dar und wird sprachlich als \(X\) impliziert \(Y\) oder ‘wenn, dann’ gebraucht. Andere Verknüpfungsformen sind die Äquivalenz(\(\leftrightarrow\)) sowie die Propositionen ‘und’ (Konjunktion \(\land\)), ‘oder’ (Disjunktion \(\lor\)) und Negation (\(\neg\)). Diese Propositionen werden auch als Junktoren, Operatoren oder Konnektoren bezeichnet.
Im folgenden werden die logischen Kombinationen aus zwei Aussagen und die Wahrheitswerte der verknüpften Aussagen (Westermann, 2000, S. 72)
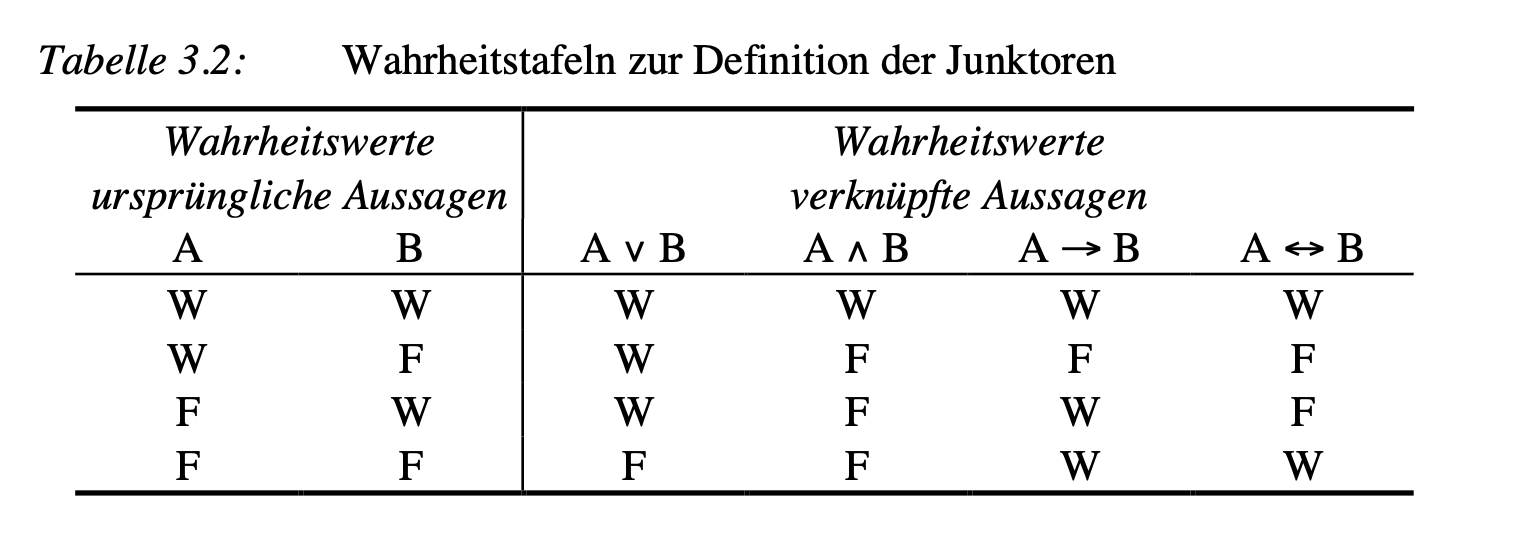
Während die Disjunktion und Konjunktion plausibel erscheinen, bedarf die Implikation weiterer Erklärungen über die Prämissen, also die gegebenen Informationen, die beim logischen Schließen vorausgesetzt (Anderson, 1996, S. 456) und nicht in Frage gestellt werden.
“Die Implikation ist durch die Wahrheitstafel so definiert, dass die Aussage \(A \to B\) nur unter einer Bedingung falsch ist: Wenn A wahr und wenn B falsch ist. Anders ausgedrückt heißt dies: „Aus Wahrem kann nicht Falsches folgen“.”(Westermann, 2000, S. 73)
Es sind die Aussage A: “Google diskriminiert Frauen” und B: “Google bezahlt Frauen ein geringeres Gehalt”. Die Aussage \(A \to B\) (Wenn Google Frauen diskriminiert, dann bezahlt Google Frauen ein geringeres Gehalt) ist definitionsgemäß nur dann falsch, falls Google Frauen diskriminiert, ihnen aber kein geringeres Gehalt zahlt.
In zwei Fällen entspricht die Logik nicht unbedingt dem Alltagsverständnis einer Wenn-Dann-Aussage:
Die Aussage “Wenn Google Frauen diskriminiert, dann bezahlt Google Frauen ein geringeres Gehalt” ist immer dann wahr, wenn ‘Google diskriminiert Frauen’ falsch ist. Darüber hinaus müssen die Aussagen nichts miteinander zu tun haben.
“Die Aussage „Wenn 2 mal 2 gleich 5 ist, dann liegt Berlin an der Elbe“ ist aussagenlogisch sinnvoll, und sie ist, da Prämisse und Konklusion falsch sind, sogar wahr” (Westermann, 2000, S. 74).
2.1 Schlussfolgerungen
Deduktive Schlüsse enthalten eine Reihe von Annahmen (Prämissen) und ein Konsequens (Dann-Teil). Aussagen wie z.B. “Wenn X wahr ist, ist Y wahr”, bilden eine Konditionalaussage in Form einer Implikation ab und beinhalten spezifische Schlussregeln.
Schlussregeln: Schlussregeln legen fest, was in der Aussage abgeleitet wird.
Eine logische Schlussregel ist der Modus ponens. Dabei wird das Konsequenz aus dem Antecedens geschlossen (A ist wahr, dann ist B wahr).
Beispiel: Aus der Prämisse \(X \to Y\) lässt der Modus ponens den Schluss zu, dass \(\frac{X}{Y}\), also aus X ist wahr wird auf Y ist wahr geschlossen.
Eine zweite Schlussregel ist der Modus tollens. Dabei wird aus der Negation des Konsequenz die Negation des Antecedens geschlossen.
Beispiel: Aus der Prämisse \(X \to Y\) lässt der Modus tollens den Schluss zu, dass \(\frac{\neg Y}{\neg X}\), also aus Y ist falsch wird X ist falsch geschlossen.
2.2 Hinreichende, notwendige und äquivalente Bedingungen
In einer bestehenden implikative Verknüpfung \(A \to B\) nach der Schlussregel des Modus ponens wird A als Prämisse der Implikation und B wird als Konklusion bezeichnet. Man sagt ‘B folgt logisch aus A’ oder ‘A impliziert B’.
2.2.1 Hinreichende Bedingung
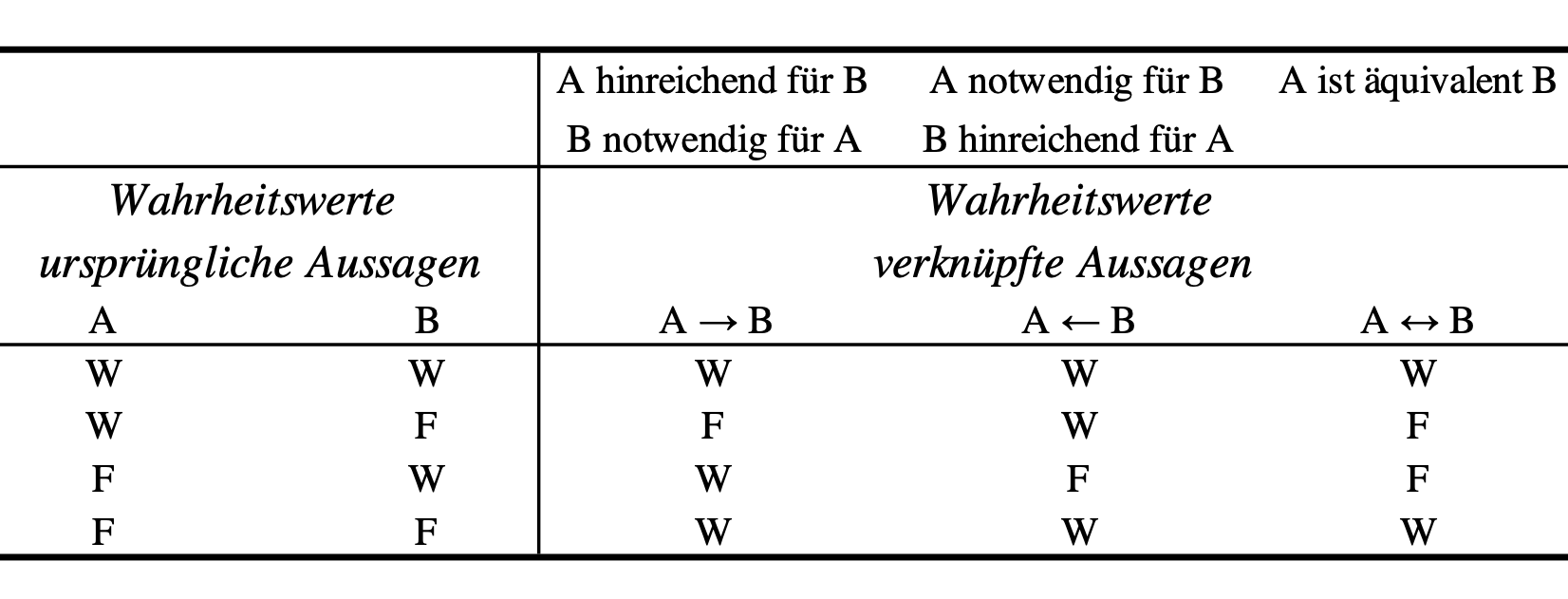
“Gilt die Aussage \(A \to B\), bezeichnet man \(A\) als hinreichende Bedingung für \(B\) und \(B\) als notwendige Bedingung für \(A\)” (Westermann, 2000, S. 74).
Nach Dul (https://bookdown.org/ncabook/advanced_nca2/glossary.html#glossary) ist die hinreichende Bedingung definiert als:
“A cause that always results in an outcome”. Logisch formuliert als \([(A \to B) \wedge A] \to B\) was den modus ponens aufzeigt, aber weil \(A \to B\) äquivalent ist zu \((\neg A) \lor B\) kann sich das Ergebnis (outcome) auch ohne die Bedingung manifestieren.
Aus der Wahrheitstabelle wird ersichtlich, dass eine Bedingung hinreichend (sufficiency) für ein outcome ist,
- wenn weder Bedingung noch Ergebnis existieren (als wahr), oder
- das Ergebnis ohne die Ursache (Bedingung) auftritt.
Der Ausdruck “hinreichend” (sufficiency) bezeichnet, wenn Dul (2016, p.18) schreibt:“If success is present in cases without the condition, X is not necessary for Y. (Dul 2016, p.18)
2.3 Notwendige Bedingung
Gilt die Aussage \(A \leftarrow B\), bezeichnet man \(A\) als notwendige Bedingung für \(B\) und \(B\) als hinreichende Bedingung für \(A\).
Die notwendige Bedingung (“necessary condition”) liegt nach Dul vor, wenn “A cause that must exist in order for the outcome to exist” (Dul’s website https://bookdown.org/ncabook/advanced_nca2/glossary.html#glossary).
\(X\) als notwendige Bedingung (necessary condition) für ein outcome \(Y\) wird formal geschrieben als \(X \Leftarrow Y\). Als Mengentheoretisch dargestellt, ist \(X\) ein “superset” (Obermenge; vgl. Dusa https://bookdown.org/dusadrian/QCAbook/analysisofnecessity.html).
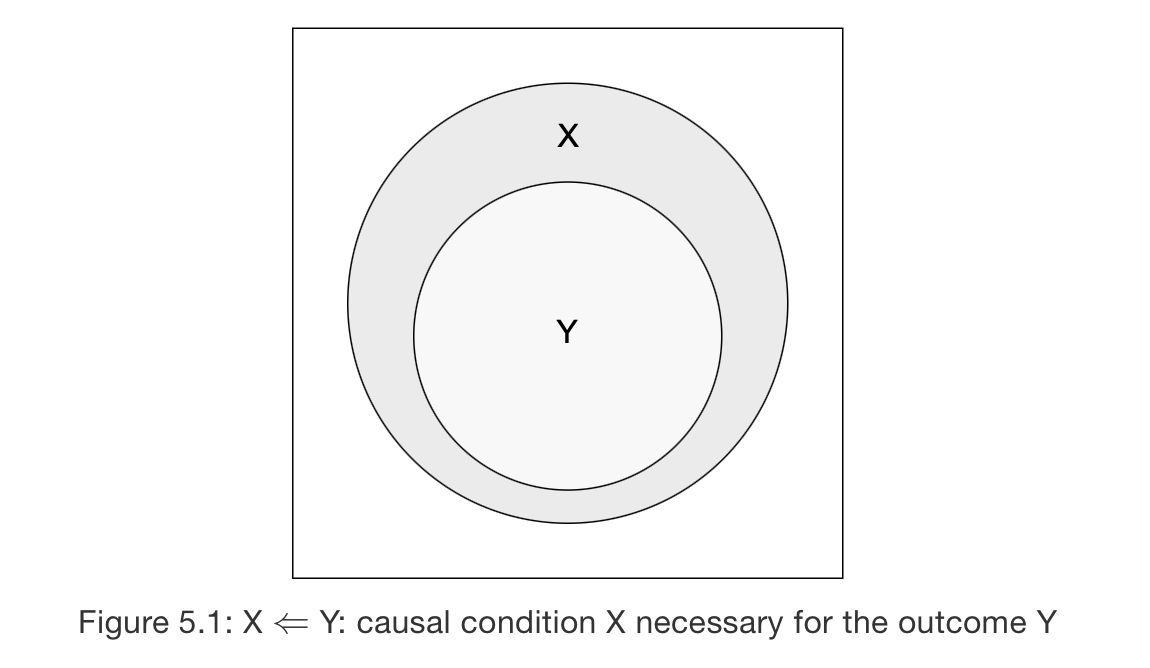
Außerdem zeigt die zweite Zeile der Wahrheitstabelle, dass A (die “Ursache”) auch eine notwendige Bedingung für B ist, wenn:
das Ergebnis (B) falsch und die Bedingung (A) wahr ist, oder
das Ergebnis (B) ist falsch und die Bedingung (A) ist falsch.
(Dul, 2016, S. 18) schreibt: “The absence of the outcome in cases without the condition is an indication of necessity of X and Y”. Übrigens ist das Fehlen der Bedingung in Fällen ohne Ergebnis auch ein Indiz für die Suffizienz von X und Y.
Beide Aussagen beinhalten das gemeinsame Fehlen von Bedingung und Ergebnis bzw. beide (Bedingung und Ergebnis) sind „wahr“. In diesen Aussagen sind also Notwendigkeit und Suffizienz äquivalent.
2.4 Äquivalenz
Ist eine Bedingung notwendig und hinreichend, bezeichnet man die Bedingung als äquivalente Bedingung (vgl. http://www.fb10.uni-bremen.de/khwagner/grundkurs2/kapitel3.aspx#_ftn2).
“Liegt eine Äquivalenz \(A \leftrightarrow B\) vor, ist \(A\) hinreichend und notwendig für \(B\), und \(B\) ist hinreichend und notwendig für \(A\).” (Westermann, 2000, S. 75)
Dies ist u.a. die typische Logik regressionsanalyitischer Verfahren.

2.5 Alternativen zum logischen Modell
Die Tatsache, dass “der Mensch … nach Vorgaben der formalen Logik schließt, dabei jedoch die Prämissen nicht erwartungskonform interpretiert” (Anderson, 1996, S. 308) ^1{ Menschen interpretieren konditionale Aussagen als bikonditionale Aussagen }. Dies wird damit erklärt, dass der Mensch nicht logisch, sondern probabilistisch schließt (Anderson, 1996, S. 308). Ein Vorteil des Probabilistischen Modells gegenüber dem logischen Modell ist, dass nur das probabilistische Modell eine Erklärung für die geringe Akzeptanz der Gültigkeit des Modus tollens bietet (Anderson, 1996, S. 309).