Kapitel 3 Strukturgleichungsmodell (SEM)

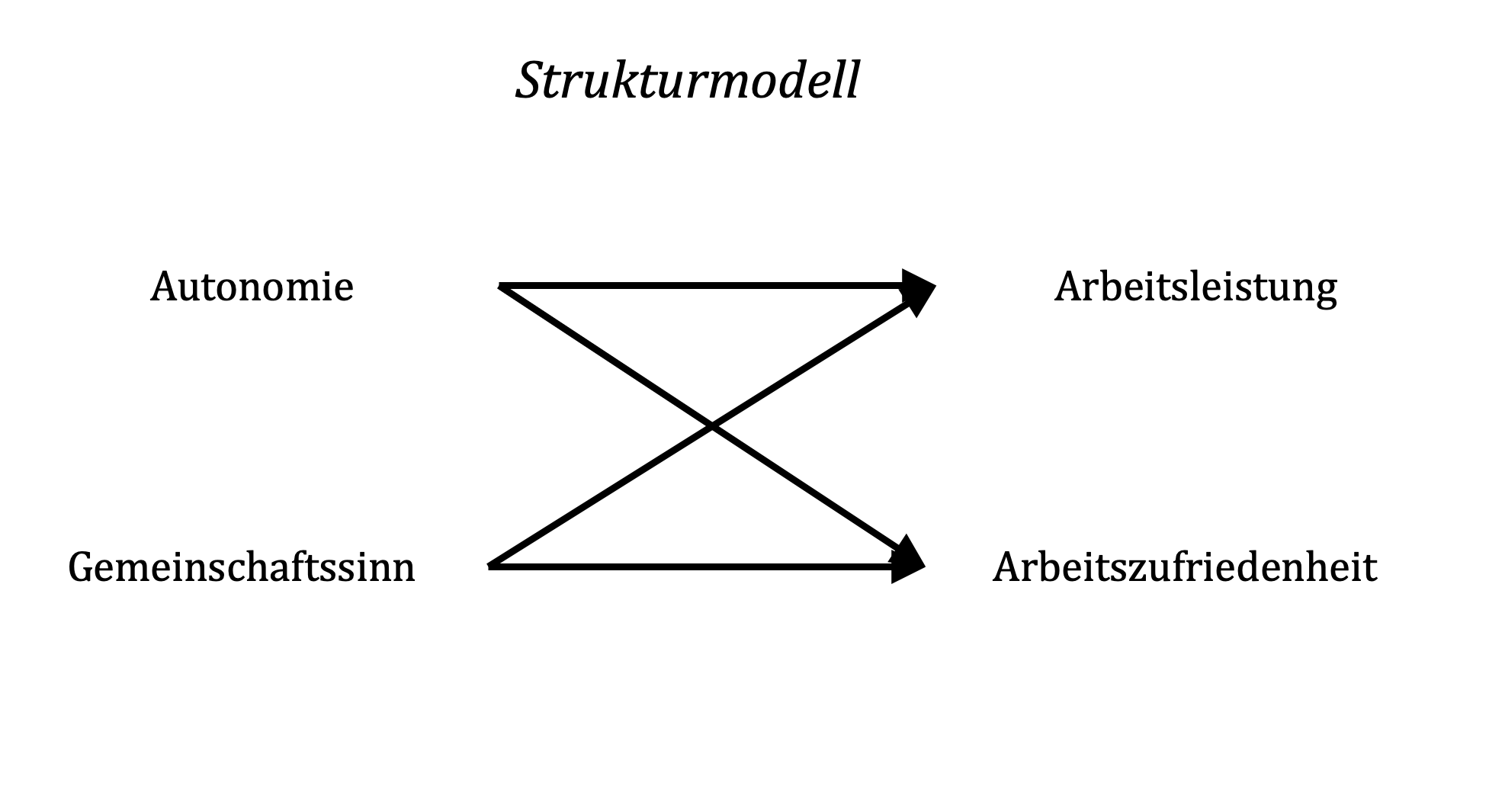
Das allgemeine Strukturgleichungsmodell kann als Weiterentwicklung der Pfadmodells angesehen werden und besteht aus zwei Teilen oder Komponenten: Der erste Teil wird als Strukturmodell bezeichnet und zeigt die angenommenen kausalen Beziehungen zwischen interessierenden Variablen auf.

3.1 Strukturmodell

Im dargestellten Beispiel sind zwei exogene Variablen (Autonomie und Gemeinschaftssinn) sowie zwei endogene Variablen (Arbeitsleistung und Arbeitszufriedenheit) abgebildet. Vor dem Hintergrund motivationaler Faktoren könnte argumentiert werden, das mit steigender Autonomie Zufriedenheit und Leistung in Arbeitsgruppen gefördert werden (z.B. Cordery, Morrison, Wright & Wall, 2010). Ebenso könnte angenommen werden, dass ein höheres Maß an Gemeinschaftssinn Leistung und Zufriedenheit fördert (z.B. Bouncken, Ratzmann, Barwinski & Kraus, 2020).

Im Gegensatz zur Pfadmodellierung werden die Variablen im Strukturgleichungsmodell als latente Variablen angesehen. Im Gegensatz zu manifesten Variablen sind sie einer direkten Messung häufig nicht zugänglich.

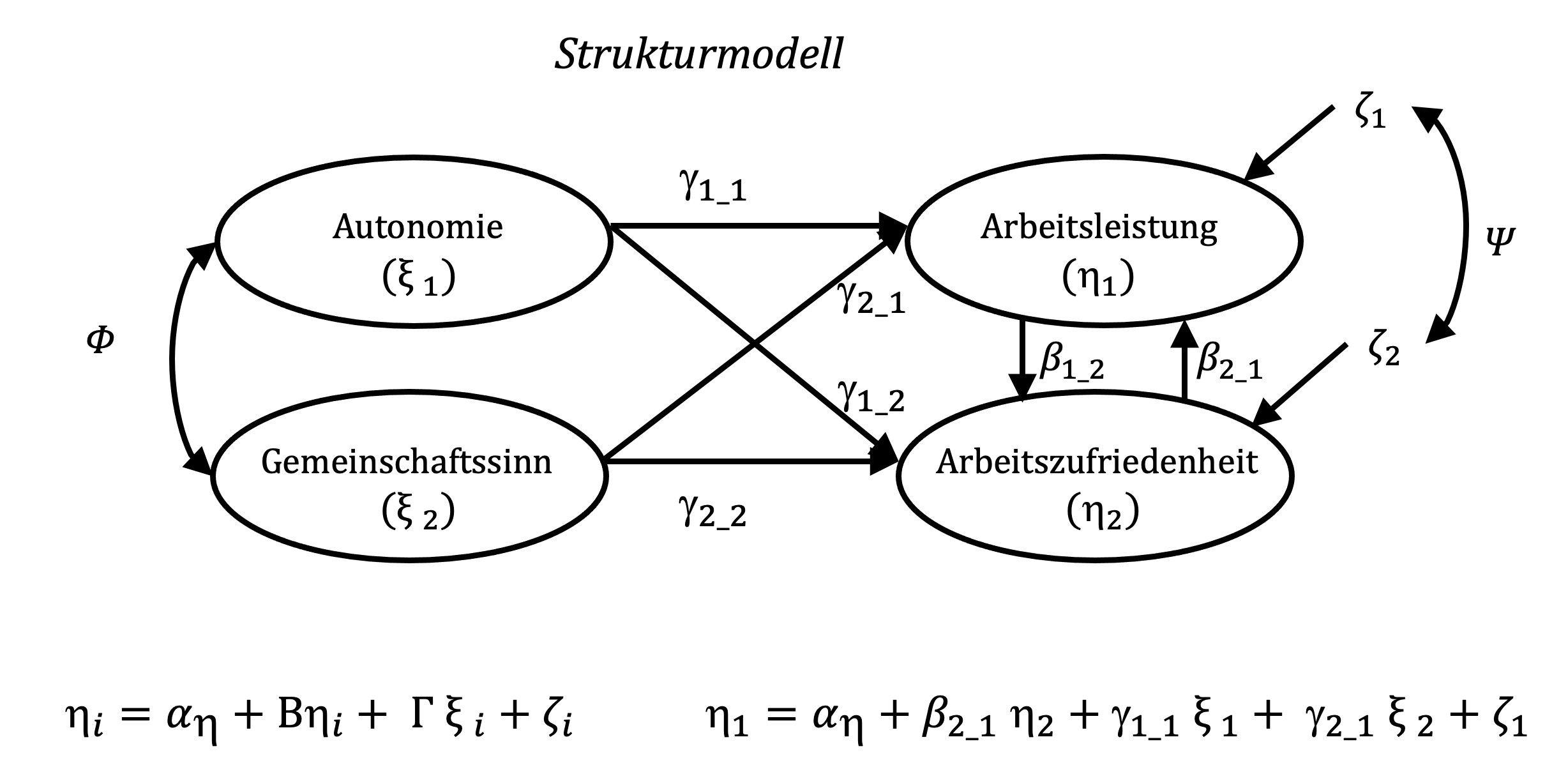
In der Darstellung von Strukturgleichungsmodellen wird diese Besonderheit dadurch gekennzeichnet, dass für latente Variablen (anstelle der Rechtecke in Pfadmodellen) Kreise oder Ellipsen verwendet werden. Exogene latente Variablen werden in der Lisrel-Terminologie der Strukturgleichungsmodellierung mit Ksi (\(\xi\)) und endogene latente Variablen mit Eta (\(\eta\)) bezeichnet (Gefen et al., 2000).

Zudem weist jede endogene latente Variable einen Term zeta (\(\zeta\)) auf, der den Teil der Varianz der endogenen latenten Variablen darstellt, der nicht durch die anderen latenten Variablen im Strukturmodell erklärt wird.

Die Koeffizienten \(\gamma\) bezeichnen die Pfadkoeffizienten, also die Stärke und je nach Vorzeichen die Richtung (positiv oder negativ) nach welcher die exogene Variable mit der endogenen Variablen zusammenhängt. Pfadkoeffizienten zwischen endogenen Variablen werden, wie bereits bekannt, mit \(\beta\) bezeichnet. Ebenfalls aus den Pfadmodellen bekannt, können die exogenen latenten Variablen frei korrelieren, was durch den Koeffizienten Phi (\(\Phi\)) berücksichtigt wird. Die Varianzen und Kovarianzen der abhängigen Variablen, bezeichnet mit Psi (\(\Psi\)), korrelieren nicht frei. Sie sind abhängig von den latenten exogenen Variablen, also dem Teil ihrer Varianz, der erklärt wird.

Das allgemeine Strukturmodell stellt die kausalen Zusammenhänge zwischen den Variablen in folgender Gleichung dar (Bollen & Pearl, 2013; Jöreskog, Olsson & Wallentin, 2016):

\[ \eta_i= \alpha_\eta + B_{\eta_i} + \Gamma_{\xi_i} + \zeta_i\] Die Darstellung der Betas und Gammas als Großbuchstaben verweist darauf, dass es sich hier genau genommen um Vektoren dieser Koeffizienten handelt.

Im Beispiel ergibt sich für die Arbeitszufriedenheit die vereinfachte Modellgleichung: \[\eta_1=\gamma_{11} \xi_1 + \gamma_{21}\xi_2 +\beta_{21}\eta_2 + \zeta_1 \]

Das Strukturmodell in Strukturgleichungsmodellen wird manchmal auch als Latentes Variablen Modell (z.B. Bollen & Pearl, 2013), Pfadmodell oder -diagramm (Jöreskog et al., 2016) oder im Kontext von Partial-Least-Squares-Strukturgleichungsmodellen (PLS-SEM; z.B. Sanchez, 2013) als Inneres Modell (inner-model) bezeichnet.

3.2 Messmodell

Wie schon angesprochen lassen sich latente Variablen nicht direkt messen, sondern indirekt über ein Messmodell. Das Messmodell bezeichnet den zweiten Teil eines Strukturgleichungsmodells und verknüpft die latenten Variablen mit manifesten Indikatoren (Bollen, 1989). An dieser Stelle reduziere ich die Beschreibung vorerst auf das Messmodell der exogenen latenten Variablen unseres Beispiels zurückkommen. Bouncken et al. (2020) nehmen an, dass der Grad an Autonomie sowie das Ausmaß an Gemeinschaftssinn, in dem ein Individuum agiert, über das Ausmaß an Zustimmung zu den folgenden sechs Items bestimmt, wobei höhere Autonomie mit höherer Zustimmung zu den ersten drei Items und geringere Autonomie mit geringerer Zustimmung zu den ersten drei Items einher gehen sollte.

Messmodell für Autonomie und Gemeinschaftssinn:

“We have strong freedom in choosing goals - rather than authorities set goals.”

“We have high autonomy in how I/we structure work – rather than authorities.”

“We autonomously develop our performance metrics – rather than authorities.”

“Working here (workspace) allows me to become part of a community.”

“Working here (workspace) allows me to overcome isolation.”

“Working here (workspace) allows me to build new friendships.”

Die entsprechende Datenmatrix sieht wie folgt aus. Die Matrix hat hier eine Dimension von 405 x 6, wobei sich die 405 auf die einzelnen Fälle im Datensatz und die sechs auf die ausgewählten Items beziehen.

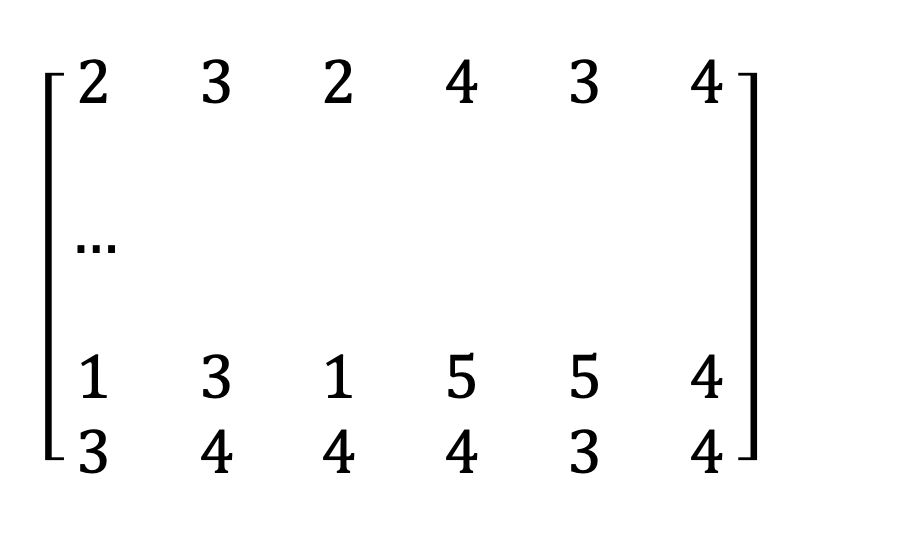
Das Messmodell entspricht hierbei dem folgenden Gleichungssystem (Bollen & Pearl, 2013; Jöreskog et al., 2016): \[ x_i=\alpha_X + \Lambda\xi_i+\delta_i \] Für die angenommenen zwei zugrunde liegenden latenten Variablen (Autonomie und Gemeinschaftssinnn) resultiert für jede Variable in der Datenmatrix (den Bewertungen zu den Items durch die Befragten) eine Gleichung der Form: \[ x_{x288}=\alpha_{x288} + \lambda_{x288} \xi_{Autonomie} + \lambda_{x288}\xi_{Gemeinschaftssinn}+ \delta_{x288} \]

Bereits bei der Einführung der Pfadmodellierung wurde angesprochen, dass es von Vorteil ist, die Beziehungen zwischen Variablen in einem System simultan als Korrelations- bzw. Kovarianz-Matrix⁴ darzustellen.

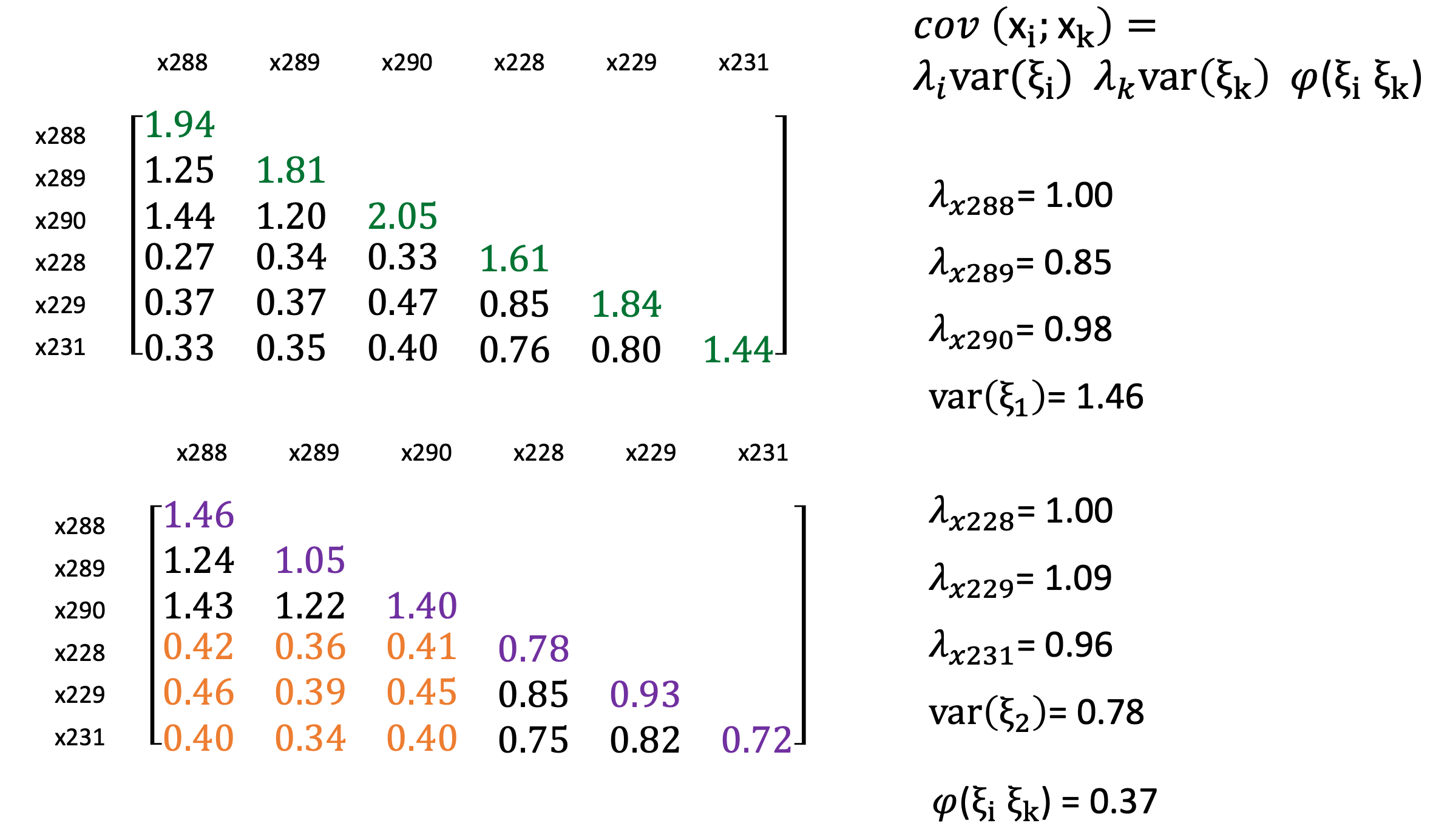
Diese Matrix hat die Dimension von 6 x 6. Wie bereits dargestellt, repräsentieren die Werte in der Diagonalen (grün markierte Werte) die Varianzen der sechs manifesten Variablen. Die übrigen Werte stellen die Kovarianz der einzelnen manifesten Variablen dar. Der Bereich über der Diagonalen zeigt die inverse also umgekehrte Form der Werte unterhalb der Diagonalen.

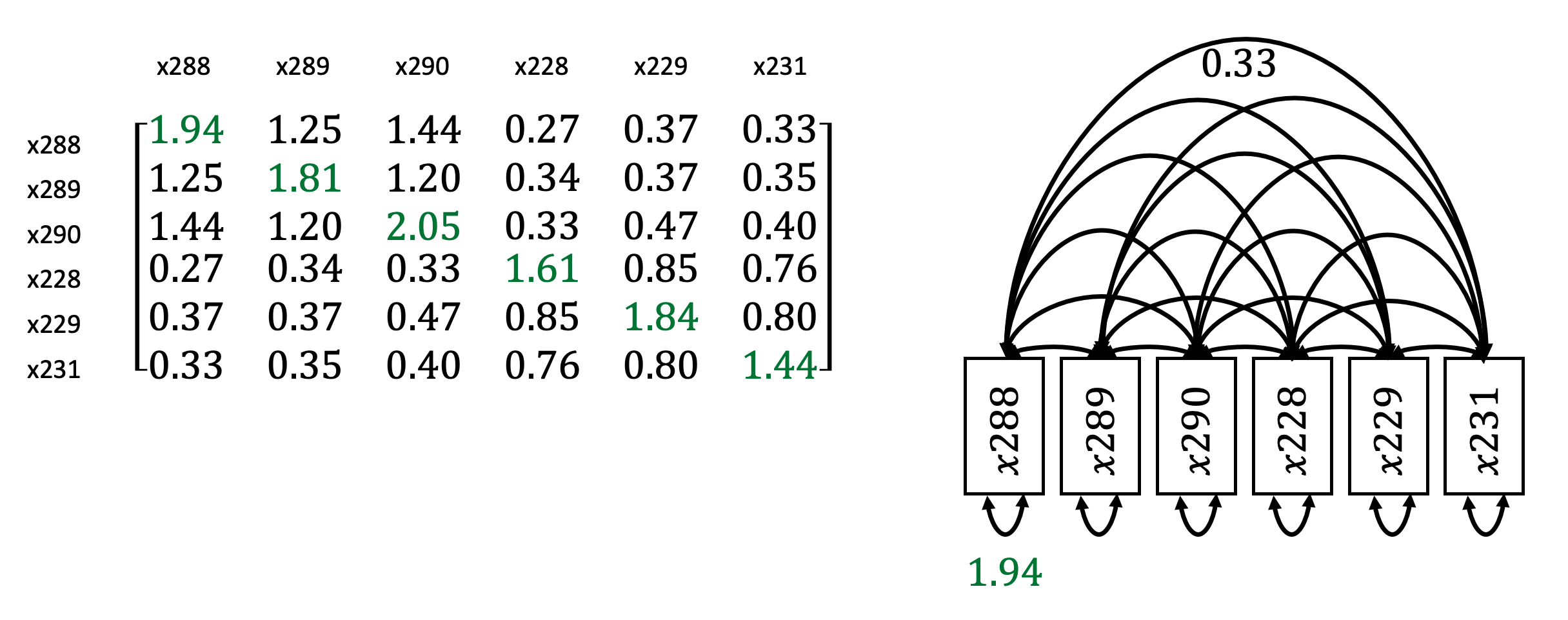
Als Pfadmodell entspricht diese Kovarianzmatrix der rechts abgebildeten Darstellung. Die Varianzen der manifesten Variablen sind unterhalb der Variablen dargestellt als Doppelpfeil einer Variable auf dieselbe und Kovarianzen sind oberhalb der Variablen dargestellt als Doppelpfeile zwischen den Variablen. Insgesamt sind hier sechs Varianzen und 15 Kovarianzen abgebildet.

Wie bereits angesprochen, geht das Modell mit latenten Variablen von drei Annahmen aus:

1. Die Varianz der manifesten Variablen wird durch unterschiedliche Ausprägungen in der zugrunde liegenden latenten Variablen bestimmt und Abweichungen gehen auf Messfehler (\(\delta\)_i) zurück. Die Varianzen der manifesten Variablen, die wir der latenten Variable Autonomie zuordnen, betragen zwischen 1.81 und 2.05 (grün markiert in der Diagonalen oben links).

Die Varianzen der manifesten Variablen, die wir der latenten Variablen Gemeinschaftssinn zuordnen, betragen zwischen 1.44 und 1.84. Unter Berücksichtigung der gleichen Skalenlänge im Fragebogen zeigt sich hier also bereits, dass die Fragen zur Autonomie eine größere Variabilität in den Antworten aufzeigen, als bei den Fragen zum Gemeinschaftssinn.

2. die Kovarianz von manifesten Variablen, die der gleichen latenten Variablen zugeordnet sind, werden durch die Varianz der latenten Variablen bestimmt. Sie sind ein Maß für die interne Konsistenz der manifesten Variablen. Die Kovarianzen der drei manifesten Variablen für Autonomie weisen Werte von 1.20 bis 1.44 auf (blau markiert).

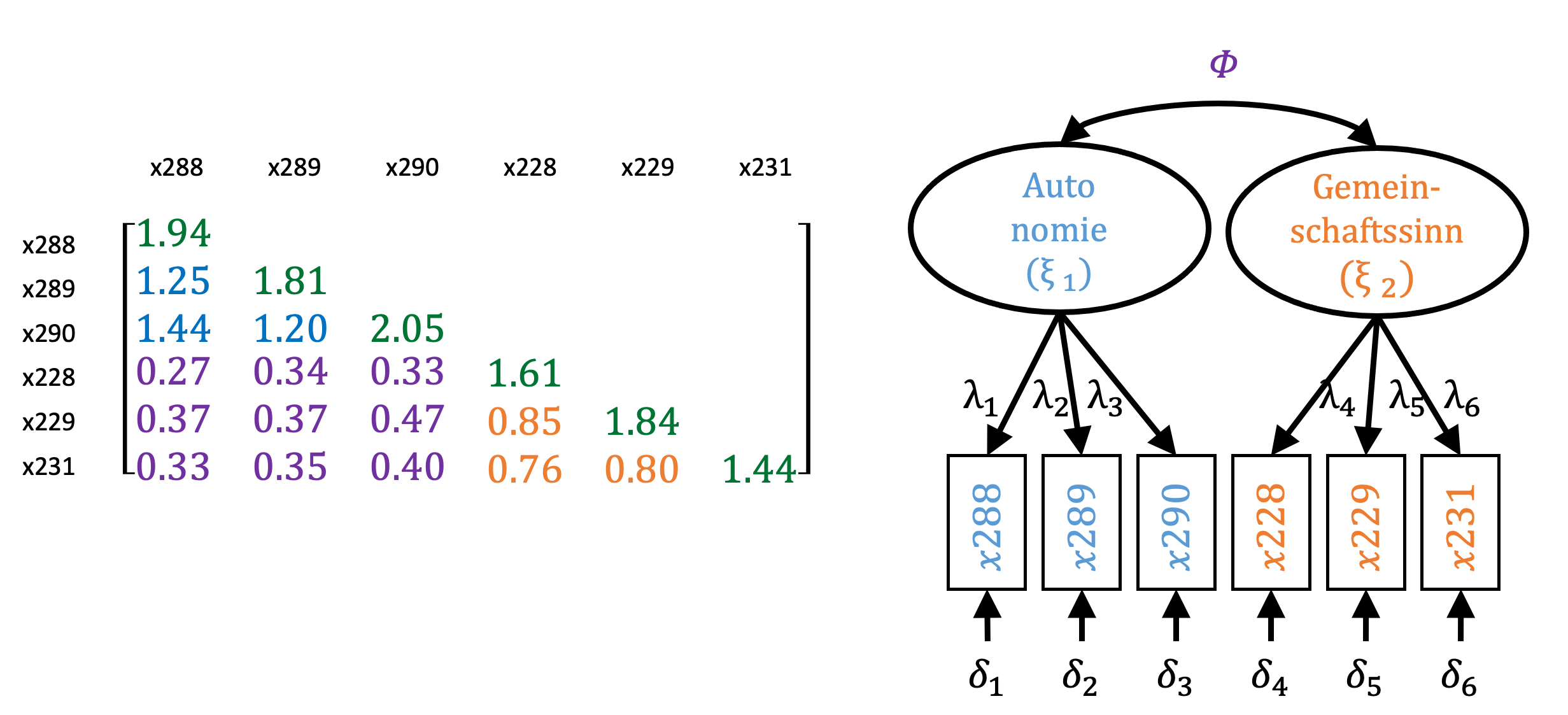
Die Kovarianzen der drei manifesten Variablen für Gemeinschaftssinn weisen Werte zwischen 0.76 und 0.85 auf (orange markiert). Aus den Anmerkungen unter 1) wird klar, warum die Kovarianzen der manifesten Variablen von Gemeinschaftssinn kleiner ausfallen.

3. die Kovarianz von manifesten Variablen, die unterschiedlichen latenten Variablen zugeordnet sind, werden durch die Kovarianz der latenten Variablen bestimmt. Im Beispiel weisen sie Werte zwischen 0.27 bis 0.47 auf und werden durch die Kovarianz der latenten Variablen Phi (\(\Phi\)) bestimmt.

Damit die Parameterschätzungen im Strukturgleichungsmodell durchführbar sind, muss die empirische Datengrundlage ausreichend viele Informationen für die Schätzung der Parameter bieten. Man spricht hier von der Identifizierbarkeit des Modells. Die Voraussetzung dafür ist es, dass die Anzahl der zu schätzenden Modellparameter höchstens so groß ist, wie die Anzahl der gegebenen Varianzen und Kovarianzen.

Im gegebenen Modell sind sechs Pfadkoeffizienten \(\lambda\), sechs Messfehlerterme \(\delta\) sowie die Kovarianz der latenten Variablen (\(\Phi\)) zu bestimmen. Es sind also 13 Parameter zu schätzen und die Kovarianzmatrix enthält sechs Varianzen und 15 Kovarianzen. Das Modell ist somit identifizierbar. Da die latenten Variablen nicht messbar sind, weisen sie keine Skalierung auf. Die Methode, die typischerweise von Programmen zur Strukturgleichungsmodellierung verwendet wird, ist die Festlegung des Pfadkoeffizienten \(\lambda\) für den ersten manifesten Indikator jeder latenten Variable auf einen Wert von eins (Jöreskog et al., 2016, S. 345).

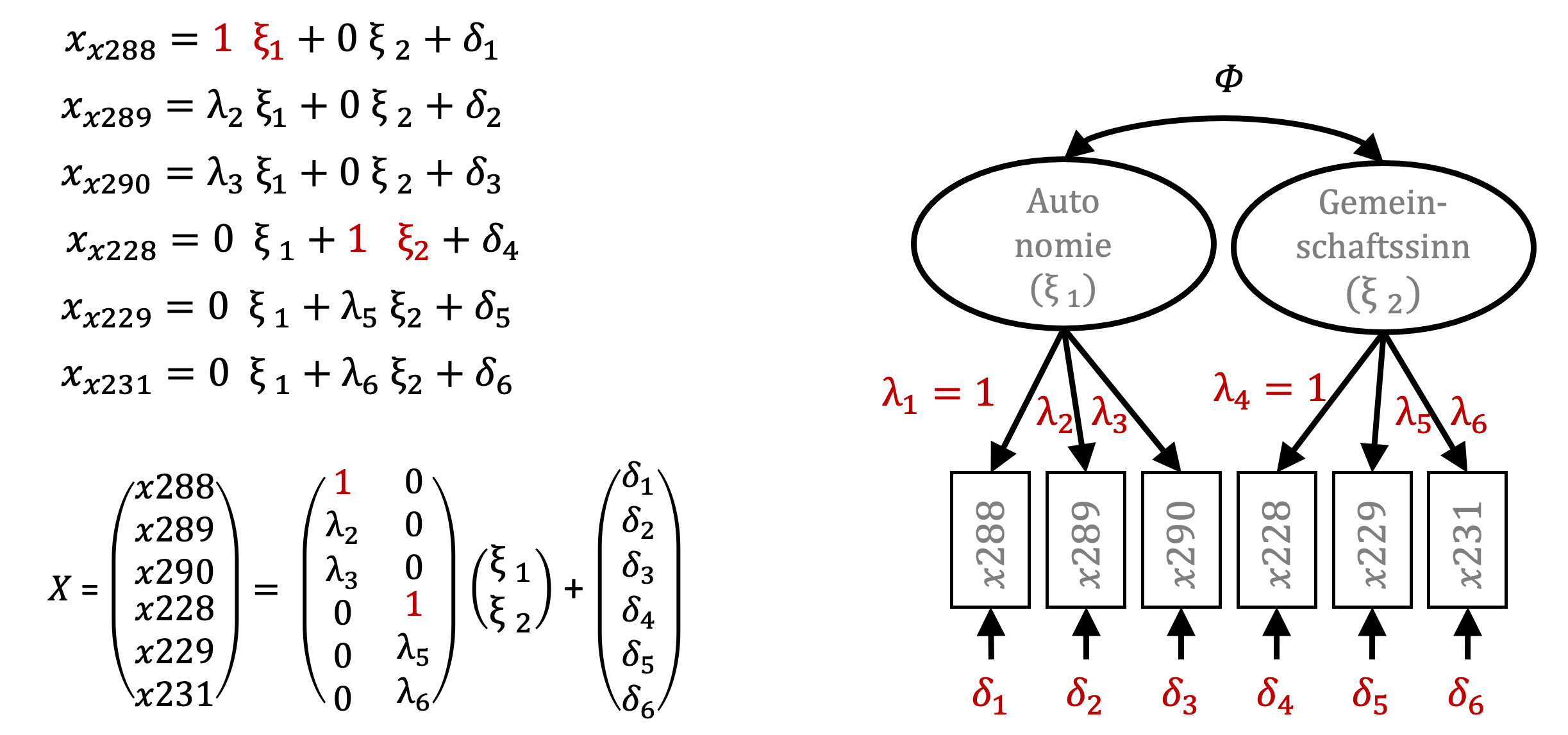
Damit dienen Mittelwert und Varianz des ersten Indikators als Referenz für Mittelwert und Varianz der latenten Variablen. Es macht daher Sinn, die manifeste Variable als ersten Indikator festzulegen, der die latente Variable am besten repräsentiert.

Die Messmodellgleichungen für die manifesten x-Variablen ändern sich entsprechend für die jeweils erste manifeste Variable, die mit einer latenten Variable verknüpft ist. In der Matrix-Form lassen sich der Vektor der manifesten Variablen X als Summe des Produktes der \(\Lambda\)-Matrix mit der Matrix der latenten Variablen und dem Messfehler-Vektor darstellen. Um die Güte von Messmodellen zu beschreiben, gibt es eine Reihe von Kriterien, auf die ich später zurückkommen werde. An dieser Stelle sein aber darauf hingewiesen, dass in jeder zuerst über das Messmodell berichtet wird. Darin sind alle latenten Variablen anhand ihrer manifesten Indikatoren zu spezifizieren und Kriterien wie Reliabilität, Validität, Modellpassung zu berichten.

Zwei weitere Matrizen sind hier noch von Bedeutung. Die Kovarianzmatrix der latenten Variablen enthält neben der Kovarianz von Autonomie und Gemeinschaftssinn die Varianzen der latenten Variablen.

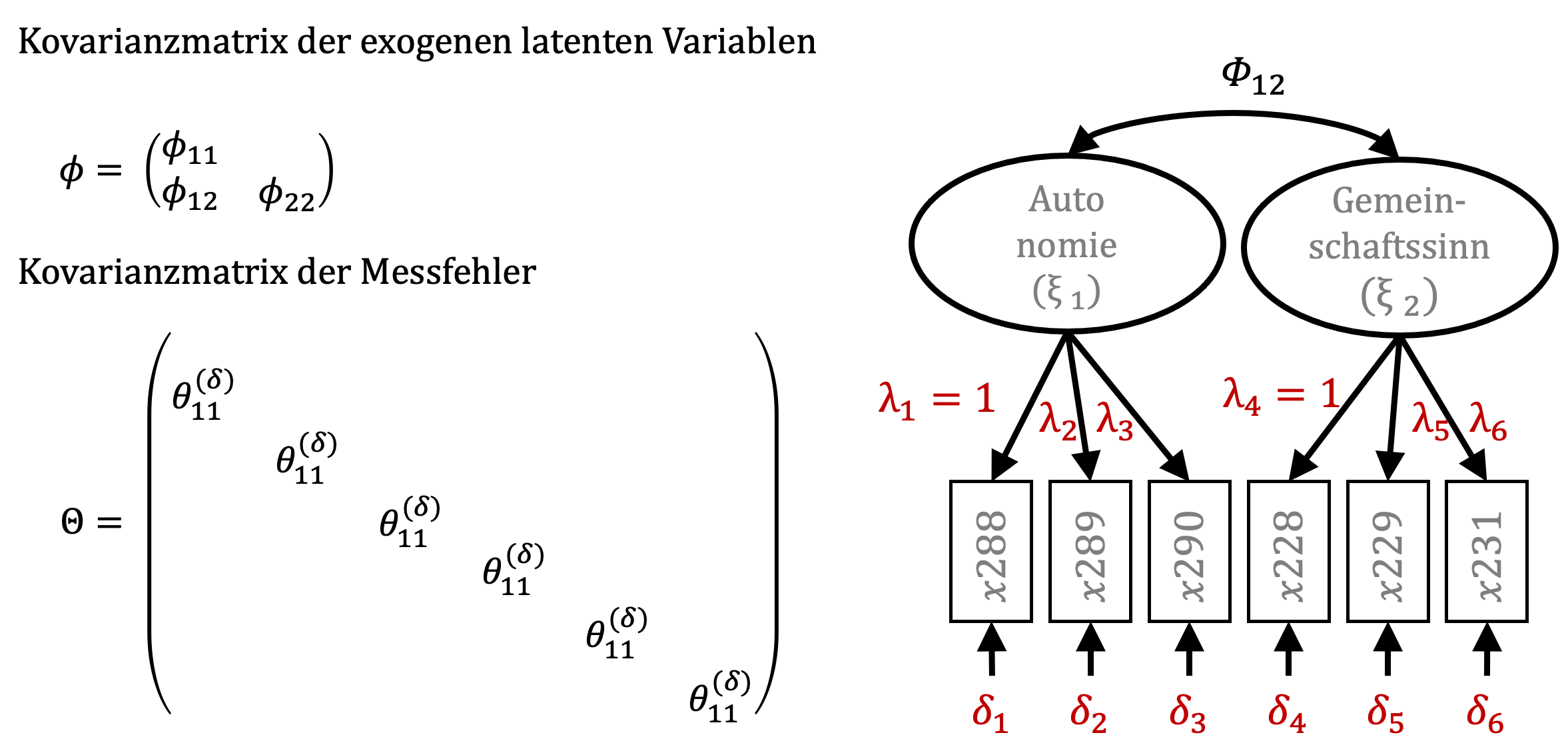
Die Kovarianzmatrix der Messfehler weist auf eine zentrale Annahme innerhalb der Strukturgleichungsmodellierung hin, dass die Messfehlerterme der manifesten Variablen keine Kovarianz aufweisen, also unabhängig voneinander sind (Bollen & Pearl, 2013). Auf der Seite der endogenen Variablen sind die Modellgleichungen nur geringfügig komplexer. Unter anderem sind hier noch die Pfadkoeffizienten gamma (\(\gamma\)) und die Störterme zeta (\(\zeta\)) einzubeziehen.

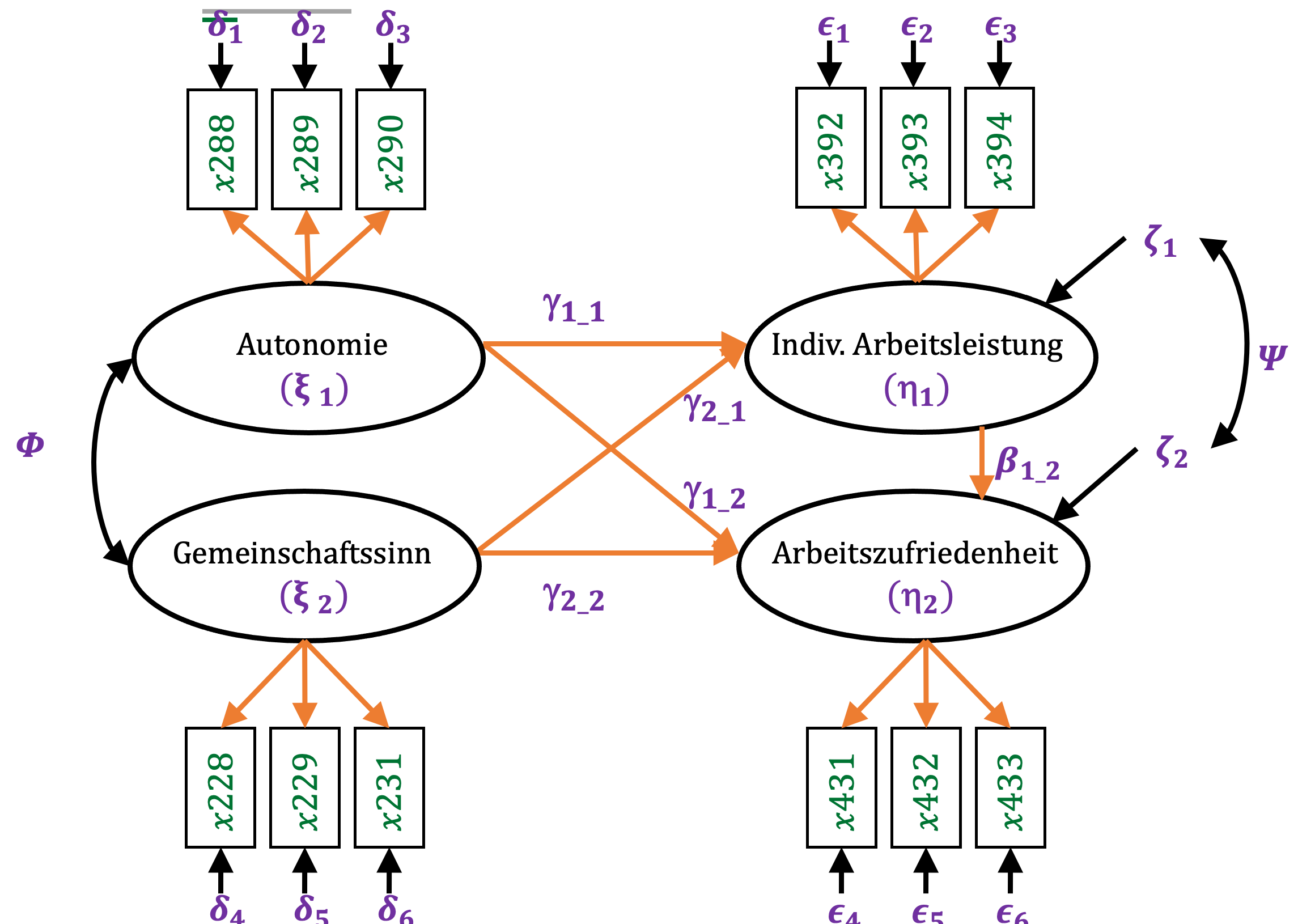
Auf dieser Abbildung sehen Sie die grafische Darstellung eines kompletten Strukturgleichungsmodells. Grün dargestellt sind die gemessenen manifesten Variablen. Orange dargestellt sind die theoretischen Annahmen des Modells. Sie weisen darauf hin, dass die Varianzen der latenten Variablen als Ursache für die Varianz in den manifesten Variablen angesehen werden. D.h. bspw. das ein hohes Maß an Individueller Arbeitsleistung die Ursache dafür ist, dass Nutzer eine hohe Zustimmung in Hinsicht auf die folgenden Aussagen geben:

Bisher ist die Arbeit hier sehr erfolgreich.

Bisher ist die Arbeit hier qualitativ hochwertig.

Bisher hat die Arbeit hier minimale/keine Nacharbeit erfordert.

Die zu schätzenden Parameter sind hier violett dargestellt. Es handelt sich um die Werte für die latenten exogenen Variablen und die latenten endogenen Variablen. Außerdem wird die Kovarianzmatrix Phi \((\Phi)\) der exogenen latenten Variablen bestimmt, die Kovarianzmatrix Psi \((\Psi)\) der nicht durch das Modell erklärten Varianzanteile zeta \((\zeta)\) der endogenen latenten Variablen, sowie die Kovarianzmatrizen der Messfehler der manifesten Variablen der exogenen latenten Variablen delta \((\delta)\) und der Messfehler der manifesten Variablen der endogenen latenten Variablen Epsilon \((\epsilon)\).

Um diese Modellparameter zu bestimmen stehen unterschiedliche iterative Schätzalgorithmen zur Auswahl. Iterativ bezeichnet dabei ein Vorgehen, bei dem wiederholte Schätzungen, die auf unterschiedlichen Gleichungsumstellungen basieren durchgeführt werden. Dabei wird diejenige Schätzung bevorzugt, welche die Annahmen am besten repliziert. Der am häufigsten verwendete Schätz-Algorithmus ist das Maximum-Likelihood-Verfahren (ML).

Über die Güte eines Modells entscheidet ein chi²-Test, der die empirische Kovarianzmatrix der manifesten Variablen mit den Prognosen der theoretischen Kovarianzmatrix vergleicht. Weist der chi²-Test ein signifikanten p-Wert auf, passen die theoretischen Annahmen nicht so gut zu der empirischen Kovarianzmatrix der manifesten Variablen.

Dieses Beispiel zeigt die empische Kovarianzmatrix der manifesten Indikatoren der latenten exogenen Variablen, wie wir sie schon betrachtet hatten. Die Diagonale spiegelt die Kovarianzen der Indikatoren, da die cov (x288, x289) gleich der cov (x289, x288) ist.

Ich stelle daher die empirischen Kovarianzen nur unter der Diagonalen dar. Die Diagonale repräsentiert die empirischen Varianzen der manifesten Variablen. Die Modellschätzung mit ML ergab die dargestellten Werte für die \(\lambda\)’s und die Varianz der exogenen latenten Variablen Ksi (\(\xi\)₁ und \(\xi\)₂).

Nach der modellimpliziten Gleichung der Kovarianz zweier Indikatoren (der gleichen latenten Variable) ergibt sich die Kovarianz von x_i und x_j als Produkt der Pfadkoeffizienten \(\lambda\)_i und \(\lambda\)_j mit der Varianz der latenten Variable ksi (\(\xi\)_ij). Die theoretische Kovarianz von x288 und x289 ergibt sich demnach aus dem Produkt von 1 mal 0.85 mal 1.46 gleich 1.24.

Die theoretischen Varianzen lassen sich als Auto-Kovarianzen bestimmen (Kenny, 2004, S. 20). Die theoretische Varianz von x288 ergibt sich demnach aus dem Produkt von 1 mal 1 mal 1.46. Es fällt auf, dass die theoretischen Varianzen kleiner sind als die empirischen Varianzen. Dies deutet darauf hin, dass ein Teil der empirischen Varianz im Modell in die Fehlerterme verschoben wird.

Zuletzt fehlen noch die theoretischen Kovarianzen der manifesten Variablen, die unterschiedlichen Variablen zugeordnet wurden. Diese Kovarianzen lassen sich aus dem Produkt der entsprechenden Pfadkoeffizienten \(\lambda\), den beiden Varianzen der latenten Variablen \(\xi\)₁ und \(\xi\)₂ sowie der Kovarianz der latenten Variablen \(\Phi\) bestimmen.

Je höher die Übereinstimmung der resultierenden Kovarianzmatrizen ist, umso besser erklärt unser Modell mit latenten Variablen die tatsächlichen Zusammenhänge zwischen den manifesten Variablen.

Deutliche Abweichungen werden durch einen signifikanten chi²-Test angezeigt. In diesem Beispiel weist der chi²-Test einen Testwert von 6.45 bei 8 Freiheitsgraden auf. Dies korrespondiert mit einem p-Wert von 0.597.

3.3 Voraussetzungen

Strukturgleichungsmodelle und insbesondere die Schätzung von Strukturgleichungsmodellen mit der Maximum-Likelihood Methode sind an einige Voraussetzungen gebunden. Wie auch in Regressionsmodellen können Stichprobenverzerrungen auftreten, wenn die Daten nicht aus einer Zufallsstichprobe stammen. Insbesondere dann, wenn Verschachtelungen der Daten bekannt sind, z.B. weil Individuen in Organisationen untersucht wurden, kann der Einfluss der Organisation auf die individuellen Bewertungen berücksichtigt werden, damit verzerrte Parameterschätzungen reduziert werden.

Der Einsatz des ML-Schätzers erfordert Intervallskalenniveau und dass die Daten multivariat normalverteilt sind. Sind die Daten nicht normalverteilt, kann die Verwendung eines robusten ML-Schätzers den Verstoß gegen diese Forderung zumindest teilweise berücksichtigen.

Die Bestimmung der Parameter im Modell geht von der Annahme aus, dass die Residuen zeta (\(\zeta\)) der endogenen Variablen sind im Durchschnitt einen Wert von Null annehmen.

Außerdem wird angenommen, dass die Residuen der endogenen Variablen keine signifikanten Korrelationen mit den exogenen Variablen des Modells aufweisen. Anderenfalls würde das angesprochene Problem der Endogenität zu falschen Schätzungen der Parameter beitragen. Darauf werde ich noch wiederholt zu sprechen kommen.

3.4 Praktischer Teil mit ‘lavaan’

Wenn wir mit der praktischen Arbeit beginnen, treten in der Regel die meisten Schwierigkeiten auf. Dabei ist es nicht immer einfach, individuelle Abhilfe zu schaffen. Ich versuche darum, nur kurz auf die häufigsten Fehler einzugehen.

Als typisches Problem hat sich immer wieder herusgestellt, dass Syntax-Code unvollständig oder falsch von den Folien abgeschrieben wurde. In dieser Version sind ausführbare Code-Beispiel und die zugehörigen Ausgaben eingebettet. Vielleicht hilf das.

Ein zweites Problem, dass recht häufig auftritt ist, dass Sie den Ordner mit den Daten auf Ihrem Rechner abspeichern, nicht auf einem Netzlaufwerk. Wenn Sie die Programmumgebung von ‘R’ öffnen, müssen Sie angeben, wo sich dieser Ordner befindet.

Für diese Zuordnung verwenden sie die Anweisung ‘setwd’, und den Verzeichnispfad zu diesem Ordner auf ihrem Rechner. In den meisten Fällen fällt es schwer, diese Verzeichnispfade richtig aufzuschreiben. Hierfür gibt es aber eine einfache Abhilfe. Sie geben die Anweisung ‘setwd (““)’ in das Terminalfenster von ‘R’ ein suchen dann auf Ihrem Rechner den Ort, an dem Sie den Ordner abgespeichert haben. Dann ziehen Sie diesen Ordner in das Terminalfenster. Dort erscheint die entsprechende Verzeichnispfadangabe.

Wenn Sie diese vollständige Anweisung mit Pfadangabe aus dem ‘R’-Terminal kopieren und in ihr Textfile speichern, brauchen Sie diesen Vorgang später nicht zu wiederholen.

Das letzte Problem, dass ich hier ansprechen möchte betrifft die Programm-Bibiotheken, die wir verwenden. Lavaan ist z.B. eine Programm-Bibiothek. Darin sind vorgefertigte Anweisungsroutinen programmiert, die uns die Strukturgleichungsmodellierung ermöglichen. Zu Beginn jeder neuen Sitzung, also wenn Sie das Programm ‘R’ ausgeschaltet hatten, werden Sie die Programm-Bibliotheken mit der Anweisung ‘Library (““)’ aufrufen.

Sollten unerwartete Fehlermeldungen auftreten, kann es sich um bestimmte Programm-Bibliotheken (sogenannte ‘packages’) handeln die mit ‘Library(““)’ aufgerufen werden, aber im Vorfeld nicht mit ‘install.packages(““)’ installiert wurden. Hinweise über Fehlfunktionen können mir bitte gemeldet werden.

# install.packages("lavaan")
library("lavaan")

An dieser Stelle wird es nun also um die konkrete Modellierung mit der Programm-Bibliothek ‘Lavaan’ in ‘R’ gehen und die direkte Prüfung anhand von realen Daten. Aus den vorausgehenden Vorträgen sollten wir an dieser Stelle bereits die Unterscheidung zwischen einer manifesten und einer latenten Variable kennen. Eine manifeste Variable ist messbar und wird als Indikator für eine nicht direkt messbare latente Variable verwendet.

In der Regel sollte eine latente Variable immer durch drei manifeste Variablen operationalisiert werden. Ich habe hier ein Modell mit drei latenten Variablen, genau genommen sind in diesem Modell zwei exogene latente Variablen, die mit ‘ksi₁’ und ‘ksi₂’ bezeichnet sind und eine endogene latente Variable, mit ‘eta’ bezeichnet. Jeder latenten Variable werde ich hier jeweils drei manifeste Variablen zuordnen.

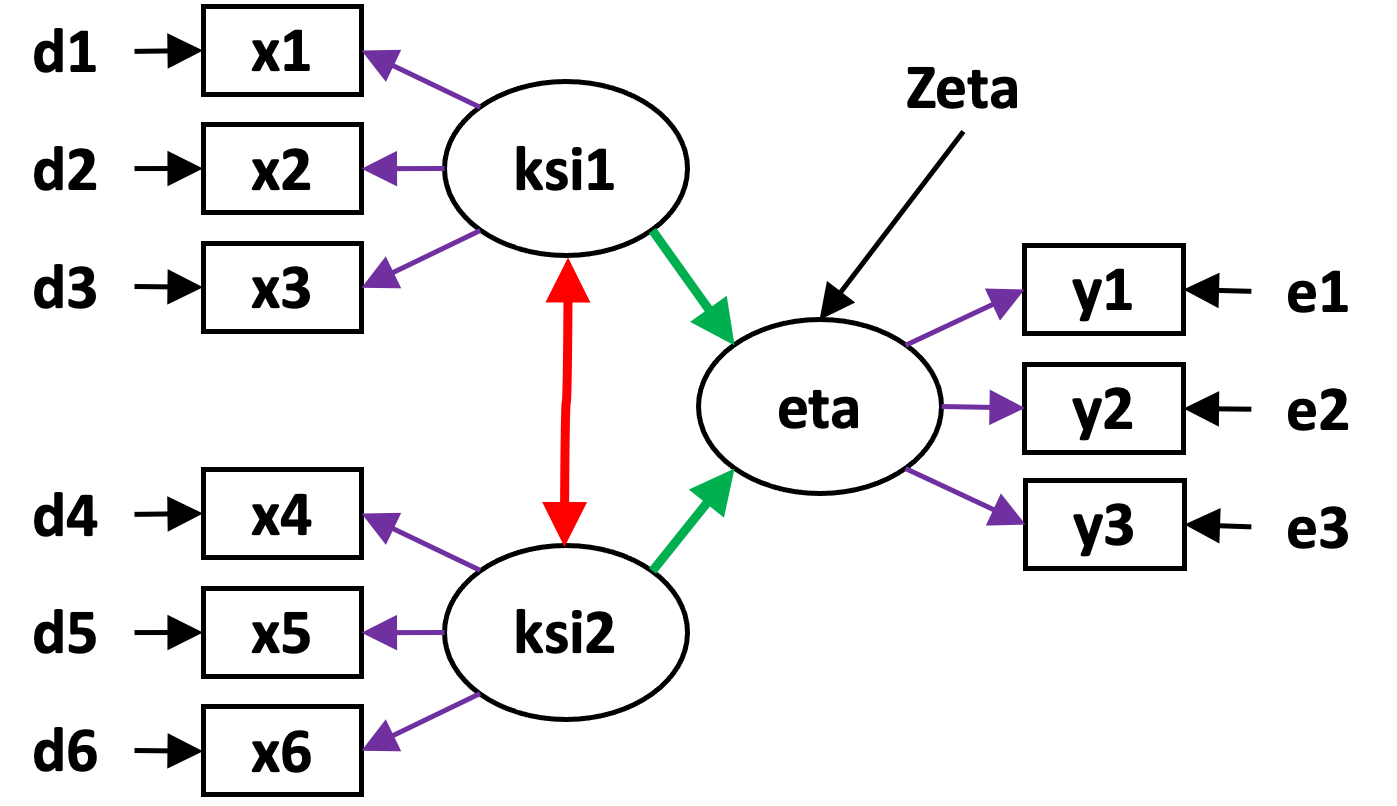
Auf der Seite der exogenen latenten Variablen sind die manifesten Indikatoren mit x1 bis x6 bezeichnet, auf der Seite der endogenen latenten Variable sind sie mit y1 bis y3 bezeichnet. Außerdem sehen Sie die Messfehler d1 bis d6 und e1 bis e3, sowie das Residuum Zeta, dass den Teil der Varianz der endogenen latenten Variable annehmen soll, der nicht durch \(\xi\)₁ und \(\xi\)₂ erklärt werden kann.

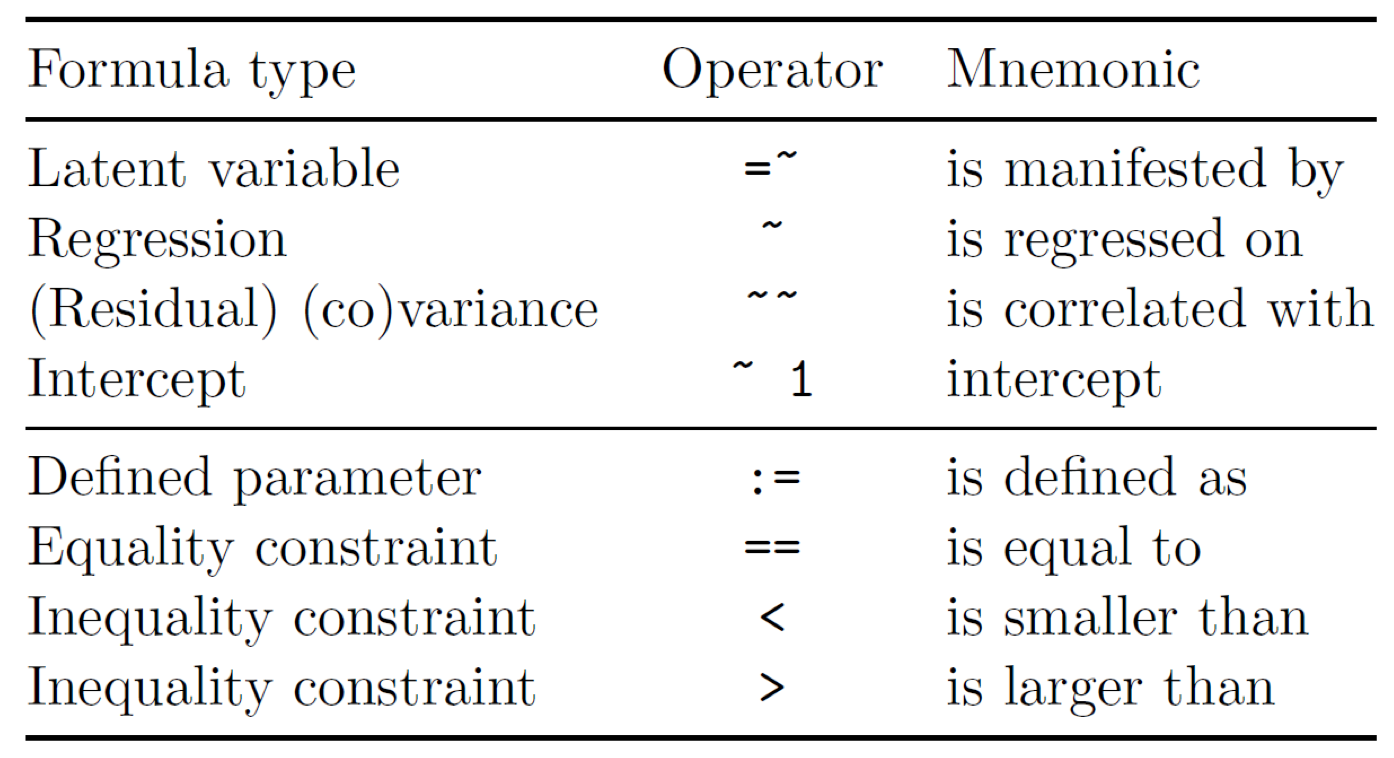
Bei der Demonstration der Pfadmodelle hatte ich bereits auf die ‘Lavaan’-Programm-Bibliothek verwiesen. In der Modellsyntax von ‘Lavaan’ legen Sie einen Namen für die latenten Variable fest, gefolgt von einem Gleichheitszeichen mit Tilde und den Namen der manifesten Variablen, die Sie durch ein Pluszeichen verbinden. Ich habe die entsprechenden Pfeile violett markiert.

Den Namen der latenten Variable können Sie sich selbst frei überlegen, ich hatte mich hier für ‘ksi1’ entschieden. Die latenten Variablen sollten aber auf keinen Fall einen Namen bekommen, der schon im Datensatz mit den manifesten Variablen vorkommt. Anderenfalls bekommen Sie später eine Fehlermeldung.

Die Bezeichnungen der manifesten Variablen entsprechen den Namen der Variablen in ihrem Datensatz, in diesem Fall x1 bis x6 und y1 bis y3.

Sie müssen dabei die Groß- und Kleinschreibung beachten, weil “R” zwischen großen und kleinen Buchstaben unterscheidet und ansonsten Fehler auftreten werden.

Um Kovarianzen zwischen latenten Variablen, dass ist hier nur der rot markierte Doppelpfeil, festzulegen, wird in der Syntax von Lavaan die Doppeltilde verwendet. Gerichtete Pfadkoeffizienten, dass sind die gerichteten Pfeile zwischen latenten Variablen mit nur einer Pfeilspitze. (hier grün markiert), werden durch eine Tilde bestimmt.

Das sind wenige, aber die grundlegend notwendigen ‘Operanten’ die Sie kennen müssen, um die grafisch dargestellte Beziehung in ein ‘Lavaan’-Modell zu übertragen.

Quelle: Rosseel (2012)

Wenn wir im Folgenden mit konkreten Daten arbeiten, greifen wir hier auf Daten aus Unternehmensbefragungen zurück, die zwischen 2017 und 2019 durch Studenten am Lehrstuhl erhoben wurden.

Dabei handelt es sich um insgesamt 423 Rückläufer aus drei Erhebungen. Bei den Befragten handelt es sich um Aussteller auf der MEDICA, einer der größten Messen im Bereich der Medizin. Diese Unternehmen agieren demnach vorwiegend in der Medizin- und Labortechnik, schließen aber auch Diagnostik und medizinischen Dienstleistungen ein.

Ein zentrales Thema dieser Befragungen war regelmäßig auch die Zusammenarbeit mit anderen Unternehmen und die Ausgestaltung der Kooperationsprozesse. Als bedeutsam für verschiedene Ergebnisse der Kooperation haben sich hier wie auch in anderen Befragungen immer wieder Vertrauen und Vertragskomplexität herausgestellt.

Die Messung von Vertrauen, wie wir sie hier eingesetzt hatten, geht auf Coote, Forrest & Tam (2003) zurück, welche diese im Kontext der Wertschöpfungsketten verwendet haben.

Die Indikatoren für Vertragskomplexität zwischen den Kooperationspartnern gehen auf die Beiträge von Cannon, Achrol & Gundlach (2000); Jap & Ganesan (2000); Liu, Li & Zhang (2010) zurück.

Beispielhaft werden wir hier die Geschäftsmodellinnvation (Business-Modell-Innovation; BMI) als Erfolgsvariable der Kooperation ansehen. Die Messung von BMI geht hier auf Bouncken & Fredrich (2016) zurück. Genau genommen messen die Aussagen die Wertschöpfung für BMI in der Beziehung.

Unsere erste Annahme ist es also an dieser Stelle, dass sich hohes Vertrauen in den Kooperationspartner in einer höheren Bewertungen der drei Indikatoren wiederfindet und das Unternehmenskooperationen, die eine hohe Vertragskomplexität aufzeigen, auch bei dem befragten Unternehmen zu einer höheren Bewertung der entsprechenden Indikatoren führen.

Wir unterstellen also eine bestimmte Erwartung an die Zusammenhänge zwischen den Indikatoren und überprüfen die richtige Zuweisung der Indikatoren zu den latenten Variablen. Dieser Prozess wird als konfirmatorische Faktorenanalyse bezeichnet.

An dieser Stelle werde ich mit den Medica-Daten arbeiten und damit beginnen, diese in die Programmumgebung einzulesen. Sie sehen hier die Anweisung dafür die Datei mit dem Namen ‘datenSS20_21.csv’ geöffnet und der Datenmatrix ‘data’ zugewiesen wird.

# Einlesen von .CSV-Tabellen mit Spaltennamen
data <- read.csv2(file='_bookdown_files/data/DatenSS20_21.csv',
                  header=TRUE)
# head(data)
nrow (data)

## [1] 423

Dabei werden die Spaltennamen für die Variablen, die in der Dateien enthalten sind mit eingelesen. Diesbezüglich werde ich eine Datei zur Verfügung stellen, welche die Zuordnung der Variablennamen zum Wortlaut im Fragebogen ermöglicht.

Wenn wir den Namen der Datenmatrix aufrufen, werden sämtliche Inhalte angezeigt. Das ist etwas chaotisch. Wenn ich nur die ersten fünf Zeilen der Datenmatrix anzeigen will verwende ich die Anweisung ‘head()’. Auch dies reduziert den Informationsgehalt nur mäßig. Um die Anzahl der Datenfälle anzeigen zu lassen, verwende ich die Anweisung ‘nrow()’. Dies bestätigt die 423 Fälle, von denen wir schon im Zusammenhang mit dem Datensatz gehört hatten.

Da ich im Folgenden nicht alle Daten verwenden werde, wähle ich mir nur neun manifesten Variablen auswählen, die für mich relevant sind. Im Datensatz sind bezeichnet mit D4, D5 und D6 für die Indikatoren von Vertragskomplexität, D7, D8 und D9 für die Indikatoren von Vertrauen und Ga7 bis Ga9 für die Indikatoren der Wertschöpfung für BMI. Diese neun Variablen kopiere ich mir in eine zweite Datenmatrix, die ich mit “subdata” bezeichne.

subdata <- data [,c("D4", "D5",  "D6", 
                    "D7", "D8",  "D9", 
                    "Ga7","Ga8","Ga9")]  

Ich lasse hier wieder die ersten Zeilen der Datenmatrix anzeigen. Als erstes fällt dabei ins Auge, dass in einem Fall anstelle von Zahlenwerten die Buchstaben ‘NA’ vorliegen. ‘NA’ steht für ‘Not-Available’. Dies bezeichnet in ‘R’ die fehlenden Werte, das heißt in diesem Fall hat der Befragte auf keine der neun Fragen geantwortet.

head(subdata)  

##   D4 D5 D6 D7 D8 D9 Ga7 Ga8 Ga9
## 1  2  2  2  4  4  4   1   2   2
## 2  4  4  4  4  4  4   4   3   3
## 3 NA NA NA NA NA NA  NA  NA  NA
## 4  4  4  4  4  5  4   4   3   3
## 5  4  4  4  3  3  3   4   4   4
## 6  5  5  5  5  5  5  NA  NA  NA

Alle anderen Zahlenwerte stehen, entsprechend der verwendeten Skalierung, für 1 bei ‘vollständiger Ablehnung’ bis 5 für ‘vollständige Zustimmung’ zu den Aussagen (Items).

Wenn wir die Kovarianzmatrix dieser Datenmatrix anzeigen wollen, ist dies nur für die Fälle möglich, in denen auch Werte vorhanden sind. Daher werde ich an dieser Stelle einen Filter verwenden, der nur die Fälle der Datenmatrix zurück behält, die auch ausgefüllt wurden.

subdata <- subdata[complete.cases(subdata),] 
nrow(subdata)

## [1] 268

Wie wir sehen sind alle Fälle mit fehlenden Werten verschwunden. Von den 423 Fällen, die wir befragt hatten, bleiben hier tatsächlich nur 268 Fälle übrig, die bei denen die Befragten auch tatsächlich auf diese neun Fragen geantwortet haben.

Mit dieser Anweisung bekommen wir die resultierende Kovarianzmatrix der neun ausgewählten Variablen.

cov(subdata)

##            D4        D5         D6          D7          D8          D9
## D4  1.4575437 1.2119738 1.01850299  0.21113533  0.15685617  0.20235899
## D5  1.2119738 1.6244061 1.13231595  0.24512270  0.22905137  0.30275588
## D6  1.0185030 1.1323159 1.50025155  0.32192968  0.23645816  0.32103527
## D7  0.2111353 0.2451227 0.32192968  0.80910056  0.49404662  0.53004640
## D8  0.1568562 0.2290514 0.23645816  0.49404662  0.75100620  0.62896193
## D9  0.2023590 0.3027559 0.32103527  0.53004640  0.62896193  0.99865839
## Ga7 0.1701045 0.1440131 0.08999944  0.01802784  0.05312622 -0.01035553
## Ga8 0.1819554 0.1490581 0.12348371 -0.02364582 -0.06108502 -0.12166695
## Ga9 0.1547320 0.1770641 0.12180670 -0.03001845 -0.05133043 -0.06839399
##             Ga7         Ga8         Ga9
## D4   0.17010453  0.18195539  0.15473196
## D5   0.14401308  0.14905808  0.17706412
## D6   0.08999944  0.12348371  0.12180670
## D7   0.01802784 -0.02364582 -0.03001845
## D8   0.05312622 -0.06108502 -0.05133043
## D9  -0.01035553 -0.12166695 -0.06839399
## Ga7  1.76911440  1.22690620  1.17778383
## Ga8  1.22690620  1.76045335  1.48841467
## Ga9  1.17778383  1.48841467  1.69572083

Die Kovarianzmatrix der Indikatoren sieht entsprechend so aus. Sie bevorzugen an dieser Stelle sicher die grafische Darstellung inklusive der zugeordneten latenten Variablen wie im Folgenden dargestellt:

3.5 Konfirmatorische Faktorenanalyse

Solche grafische Darstellung empfehle ich immer wieder, um die Modellspezifikationen zu veranschaulichen. Allein sie gibt uns keine Ergebnisse aus…

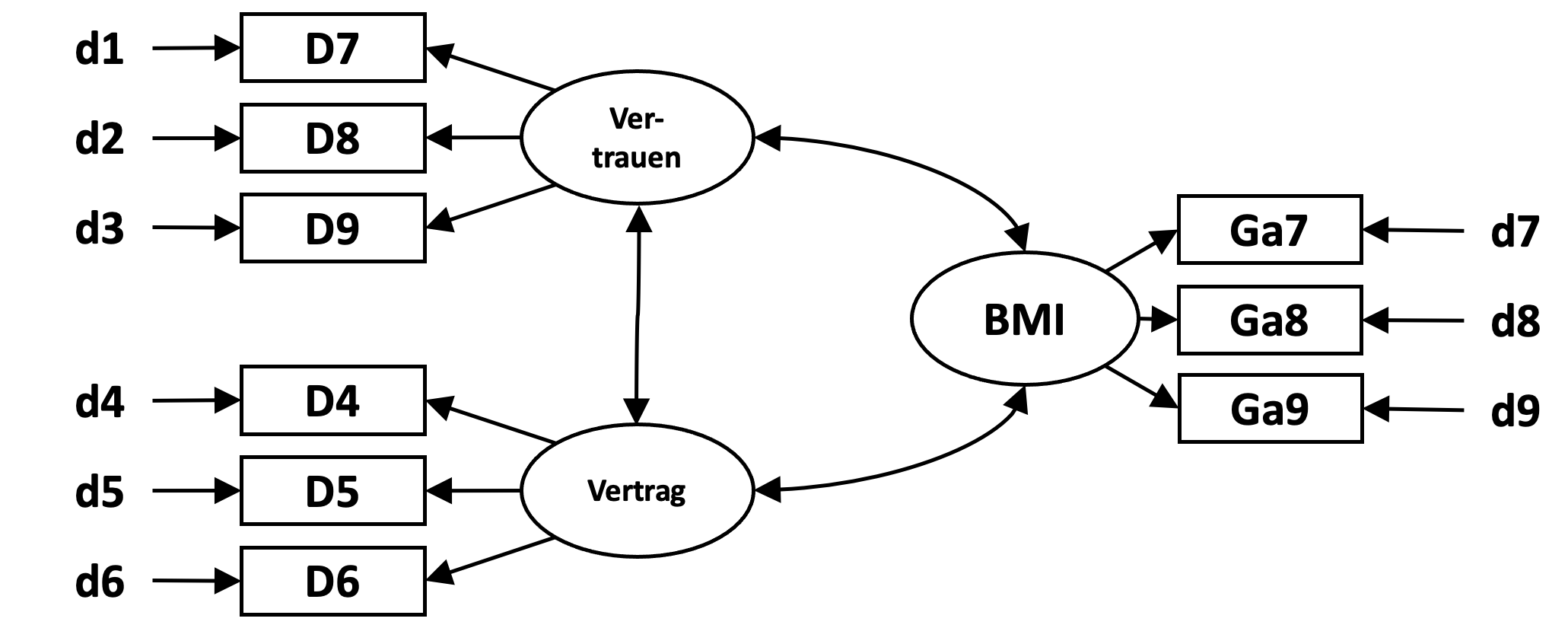
Dem oben abgebildeten Modell entspricht die unten dargestellte Modellsyntax für Lavaan. Die latenten Variablen wurden hier mit Vertrag, Vertrauen und BMI zur Bezeichnung von Wertschöpfung für Geschäftsmodellinnovation bezeichnet.

CFA <- 
  'Vertrauen =~ D7 + D8 + D9
   Vertrag =~   D4 + D5 + D6
   BMI =~       Ga7 + Ga8 + Ga9
  
   BMI ~~ Vertrauen + Vertrag
   Vertrauen ~~ Vertrag'

Erinnern wir uns zurück, mit ‘Lavaan’ definieren wir ein Modell, dass hier zum Beispiel drei Kovarianzen zwischen latenten Variablen schätzen soll und wir benötigen Daten, die hier in der Datenmatrix ‘subdata’ vorliegen.

Wir bezeichnen das Modell hier mit dem Namen ‘CFA’ und spezifizieren die Indikatoren und die Zusammenhänge zwischen den drei latenten Variablen. Die Zuordnung der Indikatoren zu den latenten Variablen erfolgt über ein ‘Gleichheitszeichen mit Tilde’ und die einzelnen Indikatoren einer latenten Variable sind durch das ‘Pluszeichen’ verbunden.

Diese Zuordnung wird für alle drei latenten Variablen durchgeführt. Die Zuweisung der Messfehler, in der Darstellung mit d1 bis d9 bezeichnet, erfolgt automatisch.

Zu bestimmen sind in diesem Modell außerdem die drei Kovarianzen zwischen den latenten Variablen, in der Darstellung oben mit Doppelpfeilen markiert und in der ‘Lavaan’-Syntax unten mit einer ‘Doppeltilde’ definiert.

Die Reihenfolge in der die latenten Variablen im Lavaan-Modell aufgeführt werden spielt keine Rolle. Es muss lediglich für jeden Doppelpfeil in der Darstellung eine Doppeltilde in der Syntax erscheinen. Es ist auch egal, ob Sie schreiben:

'Vertrag ~~ Vertrauen'

## [1] "Vertrag ~~ Vertrauen"

oder:

'Vertrauen ~~ Vertrag'

## [1] "Vertrauen ~~ Vertrag"

Es handelt sich in beiden Fällen um die gleiche Kovarianz, also den Zusammenhang zwischen zwei latenten Variablen.

Anfang und Ende der Modelldefinition werden wieder mit einem Hochkommata versehen.

Im zweiten Schritt verwenden wir wieder die Anweisung ‘SEM’ zur Modellprüfung und weisen dieser Funktion das definierte Modell und den Namen der Datenmatrix, in der sich die Daten befinden, zu.

sem(model=CFA,data=subdata)

## lavaan 0.6-10 ended normally after 30 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        21
##                                                       
##   Number of observations                           268
##                                                       
## Model Test User Model:
##                                                       
##   Test statistic                                25.677
##   Degrees of freedom                                24
##   P-value (Chi-square)                           0.370

Das Ergebnis der Modellschätzung berichtet uns zunächst, wie viele der Befragungsdaten in die Schätzung eingehen. Von den insgesamt 423 Daten scheiden 155 Datensätze aus, weil sie fehlende Daten enthalten. Das ist eine erstaunlich hohe Anzahl fehlender Werte, da meines Wissens alle drei Konstrukte in allen drei Erhebungen befragt wurden. Der Umgang mit fehlenden Werten führt an dieser Stelle jedoch zu weit vom Thema weg. Es bleiben demnach 268 Datensätze für die Schätzung unserer konfirmatorischen Faktorenanalyse übrig.

In meinem letzten Vortrag hatte ich darauf hingewiesen, dass die Übereinstimmung der theoretischen Kovarianzmatrix mit der empirischen Kovarianzmatrix anhand eines chi²-Test bestimmt wird. In diesem Fall resultiert aus dem chi²-Test ein p-Wert von 0.37. Dieser Wert weist darauf hin, dass keine signifikante Abweichung zwischen der theoretischen und der empirischen Kovarianzmatrix bestehen. Modell und Daten passen also recht gut zueinander.

Da es insbesondere bei komplexeren Datensätzen relativ schnell zu Abweichungen kommen kann, sind wurden weitere Kriterien vorgeschlagen. Dazu zählt eine Verhältnis von chi² zu den Freiheitsgraden, dass kleiner ist als 2 (Marsh, Balla & Mcdonald, 1988). In unserem Beispiel ergibt sich dementsprechend eine chi²-Ration von 25.68 geteilt durch 24 gleich 1.07.

Außerdem dem chi²-Test bestehen eine Reihe weiterer Kriterien entwickelt, um die Modellgüte zu bewerten. Die gebräuchlichsten Indizes, die im Zusammenhang mit Strukturgleichungsmodellen berichtet werden sollten sind nach Gefen, Rigdon & Straub (2011): chi² bzw. chi²-Ratio, der Comparative-Fit-Index (CFI), der Root-Mean-Squared-Error of Aproximation (RMSEA) und die standardized-root-mean-squared residuals (SRMR).

Um diese Indizes aufzuzeigen, speichern wir das Ergebnis der Modellprüfung hier unter dem Namen ‘CFA_FIT’ und nutzen die “Summary”-Anweisung, die wir um den Parameter “fit.measures=TRUE” erweitern.

CFA_FIT <- sem(model=CFA,data=subdata)
summary (CFA_FIT, fit.measures=TRUE)

## lavaan 0.6-10 ended normally after 30 iterations
## 
##   Estimator                                         ML
##   Optimization method                           NLMINB
##   Number of model parameters                        21
##                                                       
##   Number of observations                           268
##                                                       
## Model Test User Model:
##                                                       
##   Test statistic                                25.677
##   Degrees of freedom                                24
##   P-value (Chi-square)                           0.370
## 
## Model Test Baseline Model:
## 
##   Test statistic                              1438.390
##   Degrees of freedom                                36
##   P-value                                        0.000
## 
## User Model versus Baseline Model:
## 
##   Comparative Fit Index (CFI)                    0.999
##   Tucker-Lewis Index (TLI)                       0.998
## 
## Loglikelihood and Information Criteria:
## 
##   Loglikelihood user model (H0)              -3037.526
##   Loglikelihood unrestricted model (H1)      -3024.687
##                                                       
##   Akaike (AIC)                                6117.051
##   Bayesian (BIC)                              6192.462
##   Sample-size adjusted Bayesian (BIC)         6125.879
## 
## Root Mean Square Error of Approximation:
## 
##   RMSEA                                          0.016
##   90 Percent confidence interval - lower         0.000
##   90 Percent confidence interval - upper         0.053
##   P-value RMSEA <= 0.05                          0.928
## 
## Standardized Root Mean Square Residual:
## 
##   SRMR                                           0.031
## 
## Parameter Estimates:
## 
##   Standard errors                             Standard
##   Information                                 Expected
##   Information saturated (h1) model          Structured
## 
## Latent Variables:
##                    Estimate  Std.Err  z-value  P(>|z|)
##   Vertrauen =~                                        
##     D7                1.000                           
##     D8                1.166    0.094   12.350    0.000
##     D9                1.276    0.104   12.253    0.000
##   Vertrag =~                                          
##     D4                1.000                           
##     D5                1.117    0.063   17.816    0.000
##     D6                0.941    0.060   15.657    0.000
##   BMI =~                                              
##     Ga7               1.000                           
##     Ga8               1.265    0.082   15.353    0.000
##     Ga9               1.214    0.079   15.284    0.000
## 
## Covariances:
##                    Estimate  Std.Err  z-value  P(>|z|)
##   Vertrauen ~~                                        
##     BMI              -0.038    0.043   -0.877    0.380
##   Vertrag ~~                                          
##     BMI               0.121    0.069    1.763    0.078
##   Vertrauen ~~                                        
##     Vertrag           0.194    0.050    3.887    0.000
## 
## Variances:
##                    Estimate  Std.Err  z-value  P(>|z|)
##    .D7                0.386    0.041    9.494    0.000
##    .D8                0.177    0.034    5.142    0.000
##    .D9                0.311    0.046    6.780    0.000
##    .D4                0.374    0.051    7.293    0.000
##    .D5                0.274    0.055    4.994    0.000
##    .D6                0.540    0.059    9.197    0.000
##    .Ga7               0.797    0.076   10.510    0.000
##    .Ga8               0.208    0.054    3.875    0.000
##    .Ga9               0.267    0.052    5.141    0.000
##     Vertrauen         0.420    0.065    6.422    0.000
##     Vertrag           1.078    0.128    8.451    0.000
##     BMI               0.966    0.139    6.925    0.000

Der resultierende CFI von 0.999 überschreitet den empfohlenen Wert von 0.95, der RMSEA fällt mit einem Wert von 0.016 ebenfalls gut aus und der SRMR erfüllt mit einem Wert von 0.031 ebenfalls die allgemeine Anforderung. Das Modell kann also insgesamt als angemessen betrachtet werden.

An dieser Stelle habe ich einen Überblick zu diesen Kriterien aufgeführt.

Der nächste Schritt ist die Bewertung unserer theoretischen Konstrukte. Bekanntermaßen sollen theoretische Konstrukte empirisch reliabel und valide messbar sein. Die Ergebnisse einer solchen Überprüfung werden in der Regel in solcher tabellarischen Darstellung präsentiert.

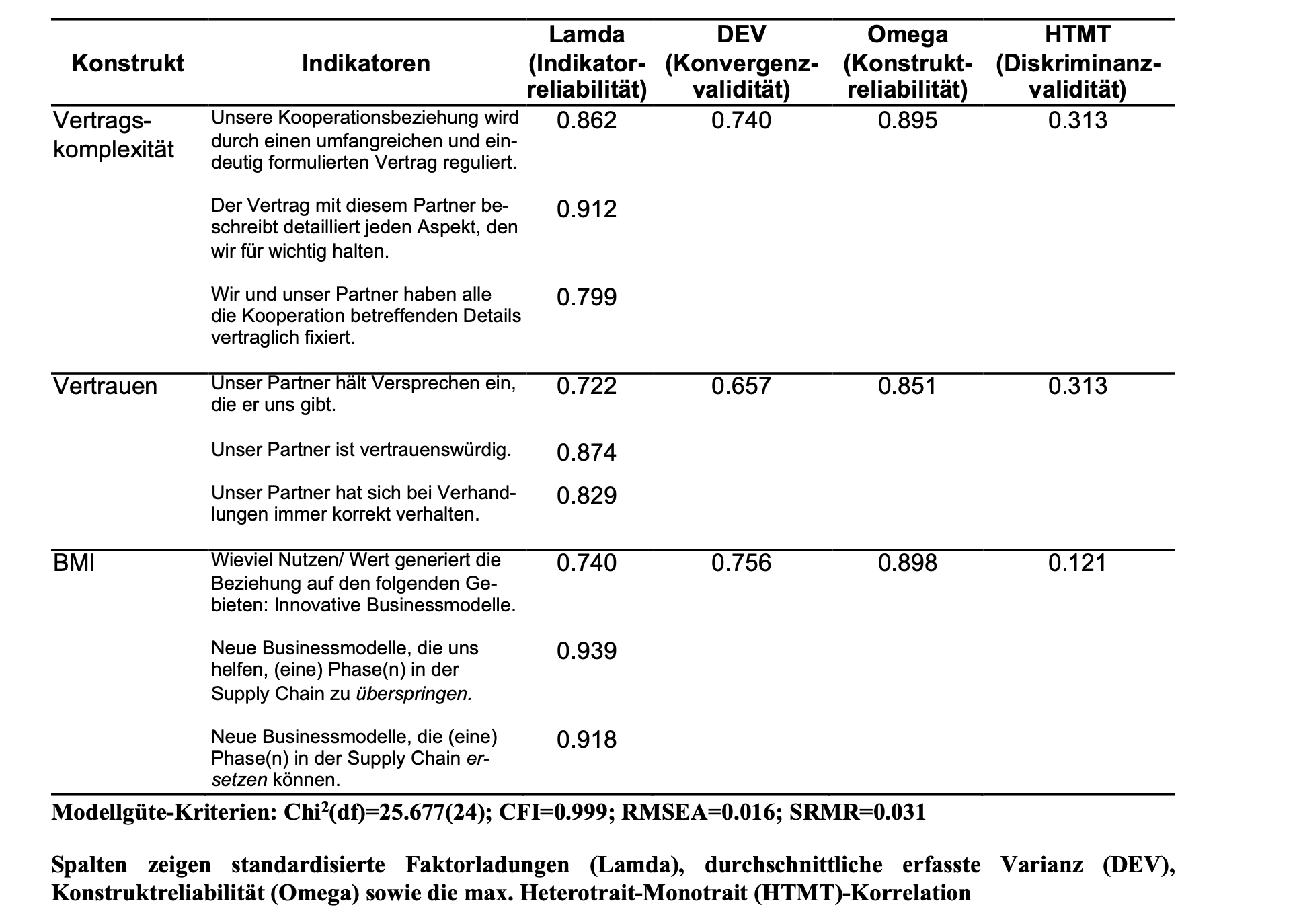
Hair, Black, Babin & Anderson (2010) sehen die Validität eines Konstruktes als gegeben an, wenn die standardisierten Faktorladungen \(\lambda_{ij}\) der Indikatoren zu ihrer latenten Variable einen Wert von 0.50 überschreiten. Andere Quellen bezeichnen die Faktorladungen als Indikatorreliabilität und fordern Werte von \(\lambda≥0.7\) (Chin, 1998). Die standardisierten Faktorladungen werden angezeigt, wenn die Anweisung ‘show (standardizedSolution())’ verwendet wird.

Die standardisierten Faktorladungen der Indikatoren von Vertragskomplexität betragen in diesem Beispiel 0.862, 0.912 und 0.799; die von Vertrauen betragen 0.722, 0.874 und 0.829. Für BMI betragen die standardisierten Faktorladungen 0.740, 0.939 und 0.918.Sie zeigen auf den ersten Blick, wie gut die Indikatoren das latente Konstrukt repräsentieren.

Ein Maß für die Validität der Indikatoren ist die durchschnittliche erfasste Varianz (Average variance extracted; AVE). Dabei handelt es sich um ein Maß, welches aufzeigt wieviel Varianz der Indikatoren mit der latenten Variable erfasst wird. Die durchschnittliche erfasste Varianz wird von Fornell & Larcker (1981) definiert als: \[\rho_{vc(\eta)}= \frac {\sum_{i=1}^{p}\lambda_{yi}^2} {\sum_{i=1}^p \lambda_{yi}^2 + \sum_{i=1}^p var(\varepsilon_i)}\] Dabei handelt es sich (vermutlich) um die standardisierten Lambda. Bagozzi & Yi (1988) formulieren in der Gleichung das Produkt der Summe der quadrierten Lambda mit der Varianz der latenten Variable (für unstandardisierte Lambda?):

\[\rho_{\overline{v}}= \frac {\sum_{i=1}^{p}\lambda_{yi}^2 { \: }{ \: } var(T)} {\sum_{i=1}^p \lambda_{yi}^2 var(T) + \sum \theta_{ii}}\] wobei T die latente Variable \(\xi\) bzw. \(\eta\) darstellt und \(\theta_{ii}\) den Varianzen der Messfehler der Indikatoren entsprechen.

Ausgehend von einem reflektiven Messmodell, verweist eine hohe AVE darauf, dass die Indikatoren zu einem hohen Anteil das gleiche Konzept (also die latenten Variable) messen. Wir sprechen hier von Konvergenzvalidität. Das Kriterium von 0.5, welches es zu überschreiten gilt stammt von Fornell & Larcker (1981, S. 46).

Die Reliabilität wird von Bollen (1980); Raykov (2001) als Anteil der wahren Varianz an der gesamten Varianz definiert und mit folgender Gleichung bestimmt: \[Reliability = \frac {(\sum_{i=1}^p \lambda_i)^2var(\eta)}{(\sum\lambda_i)^2var(\eta)+\sum var(\epsilon_i)+2 \underset{i<j}{\sum\sum} cov(\epsilon_i\epsilon_j)} = \rho_\eta\] Der letzte Term im Nenner bezieht die Kovarianz der Messfehler-Terme ein. Wenn alle Messfehler unabhängig voneinander sind, kann dieser Term ausgelassen werden (Bollen, 1980; Raykov, 2001). In aktuellen Programmen zur Strukturgleichungsmodellierung wird diese Annahme in den Voreinstellungen berücksichtigt. Der Reliabilitätskoeffizient, der durch diese Formel berechnet wird, wird von Raykov (2004) als composite reliability bzw. mit rho (\(\rho\)) bezeichnet.

Von Bagozzi & Yi (1988) als ‘composite reliability’ und von Raykov (2001) als ‘scale reliability’ bezeichnet, wird die Form (unter Annahme unabhängiger Messfehler) reduziert dargestellt als:

\[\rho_{c}= \frac {(\sum\lambda_{i})^2 var(T)} {(\sum \lambda_{i})^2 var(T) + \sum \theta_{ii}}\]

wobei T die latente Variable \(\xi\) oder \(\eta\) kennzeichnet und \(\theta_{ii}\) den Varianzen der Messfehler der Indikatoren entsprechen.

Unter Berücksichtigung der standardisierten Ladungen \(\lambda_{y_i}\) wird die Gleichung für die Reliabilität einer latenten Variable, von Fornell & Larcker (1981) als Konstruktreliabiliät rho (\(\rho\)) für das Konstrukt eta benannt und durch:

\[\rho_\eta = \frac{\sum_{i=1}^p \lambda_{yi}^2}{(\sum_{i=1}^p \lambda_{yi})^2+ \sum_{i=1}^p var(\varepsilon_i)}\] bestimmt, wobei: \[\varepsilon_i=1-\lambda_{yi}\] Von Raykov (2004) wird die reduzierte Form dargestellt als:

\[\rho_{\overline{v}}= \frac {(\sum_{i=1}^{k}b_{i})^2} {\sum_{i=1}^k b_{i}^2 + \sum _{i=1}^k \theta_{ii}}\] Die Reliabilität einer Auswahl von Messungen für eine latente Variable (composite reliability; rho (\(\rho\)) sollte einen Wert größer als 0.6 (Bagozzi & Yi, 1988) besser >0.7 (Bagozzi & Yi, 2012) erreichen. Dieses rho wird in der Programm-Bibiothek ‘semTools’ mit der Option ‘omega’ bestimmt bzw. benannt (Dunn, Baguley & Brunsden, 2014).

library(semTools)

# Average variance extracted
reliability (CFA_FIT, "ave")     

# Omega / Faktorreliabilität (composite reliability / roh )
reliability (CFA_FIT, "omega") 

# Cronbachs alpha
reliability (CFA_FIT, "alpha") # Cronbachs alpha

# Heterotrait-Monotrait
htmt(CFA, subdata)

Als letztes Kriterium führe ich hier die Diskriminanzvalidität der latenten Variable auf. Die Diskriminanzvalidität soll aufzeigen, dass die unterschiedlichen latenten Variablen eines Modells auch unterschiedliche Konstrukte repräsentieren. Das klassisches Maß für die Diskriminanz der latenten Variablen bietet die Fornell-Larcker-Ratio (Fornell & Larcker, 1981).

Dabei wurde die höchste Korrelation der latenten Variable mit anderen Modellvariablen quadriert und durch die AVE der latenten Variable geteilt. Ein resultierender Wert kleiner als eins wurde dann als Diskriminanz angesehen, weil die latente Variable mehr gemeinsame Varianz mit ihren Indikatoren teilt als mit anderen latenten Variablen des Modells.

Häufig wird in neuerer Zeit die Bestimmung der Heterotrait-Monotrait-Ration [HTMT; Henseler, Ringle & Sarstedt (2015)] gefordert. Dabei werden die Indikator-Korrelationen einer latenten Variable ins Verhältnis gebracht mit den Korrelationen dieser Indikatoren und den anderen latenten Variablen des Modells. Wir werden an dieser Stelle das HTMT -Kriterium mit Werten kleiner 0.85 einsetzen (Henseler et al., 2015).

Um die entsprechenden Indizes zu bestimmen, verwenden wir die ‘R’-Programm-Bibliothek ‘semTools’, dass wir schon bei Pfadmodellen mit Interaktion eingesetzt hatten.

Damit werden auf dem schnellsten Weg die Konvergenzvalidität der Indikatoren, also die durchschnittliche erklärte Varianz (‘ave’), die Konstruktreliabilität (Composite Reliabilität; ‘omega’), gegebenenfalls auch Cronbachs alpha (‘alpha’) und die Diskriminanzvalidität der latenten Variablen (‘HTMT’) verfügbar machen.

Diese Prozeduren wirken möglicherweise etwas umständlich, sind aber tatsächlich eine enorm wichtige Voraussetzung für eine gute Modellprüfungen, aufgrund der dann auch einzelne Hypothesen getestet werden sollen.

Wird bereits an dieser Stelle deutlich, dass die globalen Modellgüte-Kriterien nicht erreicht werden, könnte man nach alternativen Messmodellen suchen, etwa wenn man weitere Indikatoren zur Verfügung hat oder wenn einzelne manifesten Variablen sehr schiefe Verteilungen aufweisen.

Alle späteren Modifizierungen in den Zusammenhängen zwischen den latenten Variablen werden keine bessere Modellgüte aufweisen als die der konfirmatorischen Faktorenanalyse.

Schlecht bewertete Konstrukte werden nicht daran hindern, scheinbar signifikante Zusammenhänge zwischen latenten Variablen zu produzieren. Darum ist es auch so enorm wichtig bereits bei der Formulierung der richtigen Indikatoren eines theoretischen Konstruktes zu wissen, wie sich die Idee, die sich hinter diesem Konstrukt verbirgt, erfragen lässt.

Auf der anderen Seite kann ein hinreichend gutes Messmodell auch in kleineren Stichproben weiterführende Testungen durchzuführen, z.B. durch die Verwendung Werte der latenten Variablen aus der konfirmatorischen Faktorenanalyse für Pfadmodelle oder Regressionsanalysen.

Ein entscheidender Vorteil solcher Werte z.B. gegenüber Faktorwerten aus Hauptkomponenten-Faktorenanalysen besteht dann beispielsweise in der Annahme, dass diese Werte zu einem großen Teil von Messfehlern bereinigt sind.

Die Werte der latenten Variablen lassen sich speichern durch die Anweisung ‘lavPredict(CFA)’.

Ich speichere die resultierenden Werte der latenten Variablen hier in der Datenmatrix ‘fscores’ auf die ich dann in folgenden Schritten, z.B. zur bei der Darstellung von Plots oder einer Regressionsanalyse zugreifen kann.

3.6 Exkurs: Grundannahmen in Messmodellen

An dieser Stelle möchte ich einige Informationen geben, die über das absolut notwendige (für die Berechnung) hinausgehen. Bei der Entwicklung und Überprüfung von Skalen existieren Methoden mit unterschiedlichen Grundannahmen, die sich einerseits hinsichtlich ihrer Strenge gegenüber den Indikatoren und andererseits bzw. daraus resultierend auch in Hinsicht auf die Freiheitsgrade der Modellschätzung unterscheiden.

Hier möchte ich eine Übersicht von Rönkkö & Cho (2020) verwenden. Das Messmodell welches ich im letzten Video vorgestellt hatte entspricht in dieser Abbildung der Variante C - dem kongenerischen Modell mit den geringsten Anforderungen an die Güte des Messmodells.

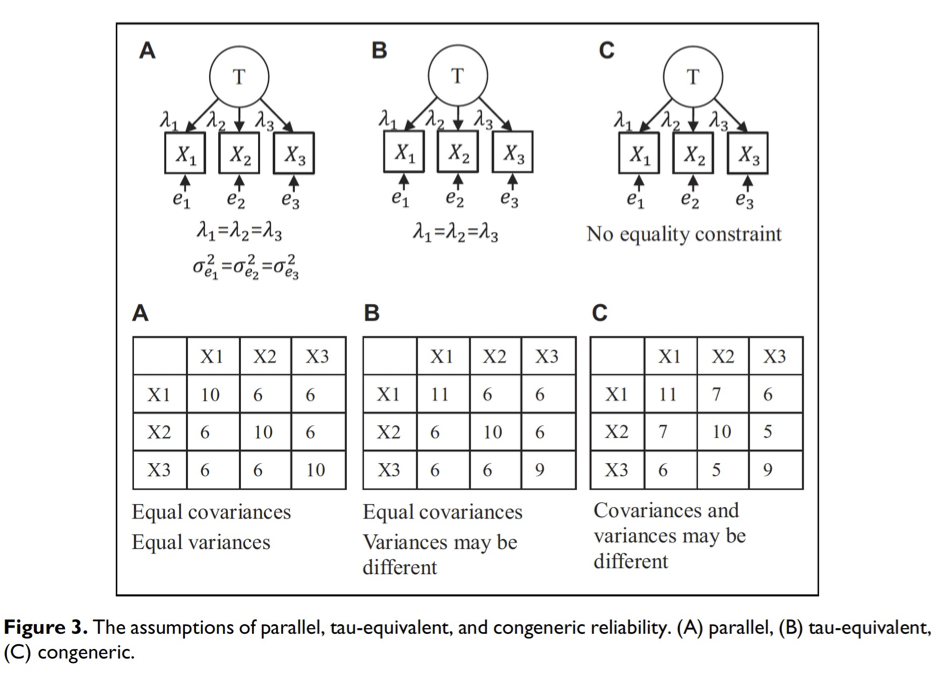
Wie bereits dargestellt, wird dabei jeweils der erste Indikator pro latenter Variable in der ersten Iteration der Modellschätzung auf eins gesetzt, um das Modell indifizierbar zu machen. Die Ladungen ‘lambda’ der übrigen Indikatoren der latenten Variable werden geschätzt.

Gleiches gilt für die Messfehler der Indikatoren ‘e’. Das kongenerische Modell erlaubt es demnach, dass sowohl die drei Schätzungen für die Ladungen ‘Lambda’ als auch die Varianzen der drei Indikatoren sich unterscheiden.

Erinnern wir uns, in der Kovarianzmatrix entsprecht die Kovarianz einer Variable mit sich selbst der Varianz dieser Variable. Die Diagonale von rechts oben nach links unten entspricht somit den Varianzen der Indikatoren.

Die Varianzen der drei Indikatoren entsprechen also 11 für den Indikator X1, 10 für Indikator X2 und 9 für Indikator X3. Die Darstellung irritiert etwas in Hinsicht auf die Ladungen “Lambda”.

Dargestellt sind hier die Kovarianzen zwischen den Indikatoren, also die Kovarianz von X1 und X2 beträgt 7, die Kovarianz von X1 und X3 beträgt 6 und die Kovarianz von X2 und X3 beträgt 5.

Literatur

Bagozzi, R. P. & Yi, Y. (1988). On the evaluation of strucutral equation models. Journal of Academy of Marketing Science, 16(1), 74–94. https://doi.org/10.1007/BF02723327

Bagozzi, R. P. & Yi, Y. (2012). Specification, evaluation, and interpretation of structural equation models. Journal of the Academy of Marketing Science, 40(1), 8–34. https://doi.org/10.1007/s11747-011-0278-x

Bollen, K. A. (1980). Issues in the Comparative Measurement of Political Democracy. American Sociological Review, 45(3), 370–390. https://doi.org/10.2307/2095172

Bollen, K. A. (1989). Structural Equations with Latent Variables. Book, New York: John Wiley; Sons Inc.

Bollen, K. A. & Pearl, J. (2013). Eight Myths About Causality and Structural Equation Models. In S.L. Morgan (Hrsg.), Handbook of Causal Analysis for Social Research (S. 301–328). New York: Springer. https://doi.org/10.1007/978-94-007-6094-3_15

Bouncken, R. B. & Fredrich, V. (2016). Business model innovation in alliances: Successful configurations. Journal of Business Research, 69(9), 3584–3590. https://doi.org/http://dx.doi.org/10.1016/j.jbusres.2016.01.004

Bouncken, R., Ratzmann, M., Barwinski, R. & Kraus, S. (2020). Coworking spaces: Empowerment for entrepreneurship and innovation in the digital and sharing economy. Journal of Business Research, 114, 102–110. https://doi.org/https://doi.org/10.1016/j.jbusres.2020.03.033

Cannon, J. P., Achrol, R. S. & Gundlach, G. T. (2000). Contracts, norms, and plural form governance. Journal of the Academy of Marketing Science, 28(2), 180–194. https://doi.org/10.1177/0092070300282001

Chin, W. W. (1998). The partial least squares approach for structural equation modeling. In G.A. Marcoulides (Hrsg.), Modern methods for business research (S. 295–336). New Jersey: Lawrence Erlbaum.

Coote, L. V., Forrest, E. J. & Tam, T. W. (2003). An investigation into commitment in non-Western industrial marketing relationships. Industrial Marketing Management, 32(7), 595–604. https://doi.org/https://doi.org/10.1016/S0019-8501(03)00017-8

Cordery, J. L., Morrison, D., Wright, B. M. & Wall, T. D. (2010). The impact of autonomy and task uncertainty on team performance: A longitudinal field study. Journal of Organizational Behavior, 31(2-3), 240–258. https://doi.org/10.1002/job.657

Dunn, T. J., Baguley, T. & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105(3), 399–412. https://doi.org/https://doi.org/10.1111/bjop.12046

Fornell, C. & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39–50.

Gefen, D., Rigdon, E. E. & Straub, D. (2011). Editor’s Comments: An Update and Extension to SEM Guidelines for Administrative and Social Science Research. MIS Quarterly, 35(2), iii–xiv. https://doi.org/10.2307/23044042

Gefen, D., Straub, D. W. & Marie-Claude, B. (2000). Structural Equation Modeling Techniques and Regression: Guidelines for Research Practice. Communications of the Association for Information Systems (AIS), 4(7), 1–78.

Hair, J. F., Black, W. C., Babin, B. J. & Anderson, R. E. (2010). Multivariate data analysis (7. Auflage). Upper Saddle River, N.J.: Pearson.

Henseler, J., Ringle, C. M. & Sarstedt, M. (2015). A new criterion for assessing discriminant validity in variance-based structural equation modeling. Journal of the Academy of Marketing Science, 43(1), 115–135. https://doi.org/0.1007/s11747-014-0403-8

Jap, S. D. & Ganesan, S. (2000). Control Mechanisms and the Relationship Life Cycle: Implications for Safeguarding Specific Investments and Developing Commitment. Journal of Marketing Research, XXXVII, 227–245.

Jöreskog, K. G., Olsson, U. H. & Wallentin, F. Y. (2016). Structural Equation Models (SEM) with Latent Variables. Multivariate Analysis with LISREL (S. 341–378). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-33153-9_8

Kenny, D. A. (2004). Correlation and Causality. Book, New York, NY: John Wiley; Sons Inc.

Liu, Y., Li, Y. & Zhang, L. (2010). Control mechanisms across a buyer–supplier relationship quality matrix. Journal of Business Research, 63(1), 3–12. https://doi.org/10.1016/j.jbusres.2009.01.005

Marsh, H., Balla, J. & Mcdonald, R. (1988). Goodness-of-fit indexes in confirmatory factor analysis : The effect of sample size, 103, 391–410. https://doi.org/10.1037/0033-2909.103.3.391

Raykov, T. (2001). Estimation of congeneric scale reliability using covariance structure analysis with nonlinear constraints. British Journal of Mathematical and Statistical Psychology, 54(2), 315–323. https://doi.org/10.1348/000711001159582

Raykov, T. (2004). Point and Interval Estimation of Reliability for Multiple-Component Measuring Instruments via Linear Constraint Covariance Structure Modeling. Structural Equation Modeling: A Multidisciplinary Journal, 11(3), 342–356. https://doi.org/10.1207/s15328007sem1103_3

Rönkkö, M. & Cho, E. (2020). An Updated Guideline for Assessing Discriminant Validity. Organizational Research Methods, 0(0), 1–42. https://doi.org/10.1177/1094428120968614

Rosseel, Y. (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1–36.

Sanchez, G. (2013). PLS Path Modeling with R. Berkeley: Trowchez Editions.

Wright, S. (1921). Correlation and causation. Journal of Agricultural Research, 20(3), 557–585. Journal Article,.

---

4. Die Möglichkeit der Matrixrepräsentation wurde durch Pearson (Wright, 1921) entwickelt. In einer Korrelationsmatrix entsprechen die Diagonalen einem Wert von 1 und die darüber liegenden Korrelationen sind die invertierte / transponierte Form der darunter liegenden Korrelationen der Wertepaare. In einer Kovarianz-Matrix entsprechen die Werte der Diagonalen der Kovarianz der Variablen mit derselben Variablen, was der Varianz dieser Variablen entspricht.↩︎