Kapitel 2 Pfadmodellierung
Die Idee der Pfadmodellierung geht auf die Arbeiten des Biologen und Genetikers Sewall Wright (1889-1988) in den 1920-iger Jahren zurück (Pearl & Mackenzie, 2018, S. 6) . Obwohl seine Ideen eine Grundlage für die aktuellsten Methoden der kausalen Inferenz darstellen (oder gerade deshalb) wurden sie erst in den 1960-iger Jahren aufgegriffen und weiterentwickelt.
Quelle: (Pearl & Mackenzie, 2018, S. 74)
Wright (1921) teilte die Annahme, dass das Experiment die ideale Methode der Wissenschaft darstellt, um den direkten Einfluss einer Variablen (Bedingung) auf eine andere zu bestimmen und das hierfür alle anderen möglichen Ursachen von Variationen zu eliminieren sind.
Angesichts der Realität, dass in der Biologie eine Reihe von Ursachen für Variationen (in Form von Merkmalen oder Bedingungen) existieren, die sich außerhalb der Kontrolle des Wissenschaftlers befinden und komplexe Interaktionen aufweisen, leitet er ab, dass der Wert der Korrelation zweier Variablen vielmehr als das Resultat aller verbundenen Einflüsse angesehen werden kann.
Vor diesem Hintergrund entwickelte Wright (1921) die Methode der Pfade bzw. der Pfadabhängigkeit. Die Methode ist somit ein Versuch, den direkten Einfluss entlang von Pfaden in einem System von Beziehungen zu messen und zu bestimmen, zu welchem Grad ein bestimmter Effekt durch spezifische Ursachen bestimmt wird.
Dabei gehen sowohl die Kenntnis der Korrelation zwischen Variablen in einem System und das verfügbare Wissen über kausale Beziehungen ein (Wright, 1921). In Situationen, in denen kausale Zusammenhänge unsicher sind, kann die Methode verwendet werden, um die logischen Konsequenzen einer bestimmten Hypothese zu finden.
Wir hatten bereits angesprochen, dass die Korrelation zwischen zwei Variablen mit zwei statistischen Kennwerten verbunden ist: den Stichprobenmittelwerten von X und Y sowie den Standardabweichungen von X und Y. Die Verwendung des Korrelationskoeffizienten beruht zudem auf der Annahme, dass eine lineare Beziehung zwischen X und Y existiert, so dass eine gegebene Änderung in der einen Variablen immer mit einer konstanten Änderung in der anderen Variablen einhergeht.
Der Wert des Korrelationskoeffizienten kann innerhalb des Bereiches von -1 bis +1 liegen. Der Zahlenwert der Korrelation entspricht damit der Abweichung einer Variablen von ihrem Stichprobenmittelwert, die einer gegebenen Abweichung der anderen Variablen entspricht.
2.1 Exkurs: Mengentheoretische Perspektive
Um dies zu veranschaulichen werden häufig Mengendiagramme (sogenannte VENN-Diagramme) eingesetzt. Auf dieser ersten Abbildung sind drei unterschiedlich große Kreise dargestellt. Die Größe der Kreise symbolisiert die Varianz, also die Abweichungen der einzelnen Messungen vom Mittelwert.
Mathematisch ausgedrückt wird die Varianz definiert als:
\[\sigma^2 = s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i- \overline{x})^2\]
Der erste Kreis ist extrem klein (nahezu ein Punkt). In diesem Fall liegt eine sehr kleine Varianz vor, d.h. die einzelnen Messungen entsprechen nahezu dem Mittelwert bzw. es könnte sich um eine Konstante handeln. Der zweite und der dritte Kreis stehen für größere Varianzen, also größere Abweichungen der einzelnen Messungen vom Mittelwert.
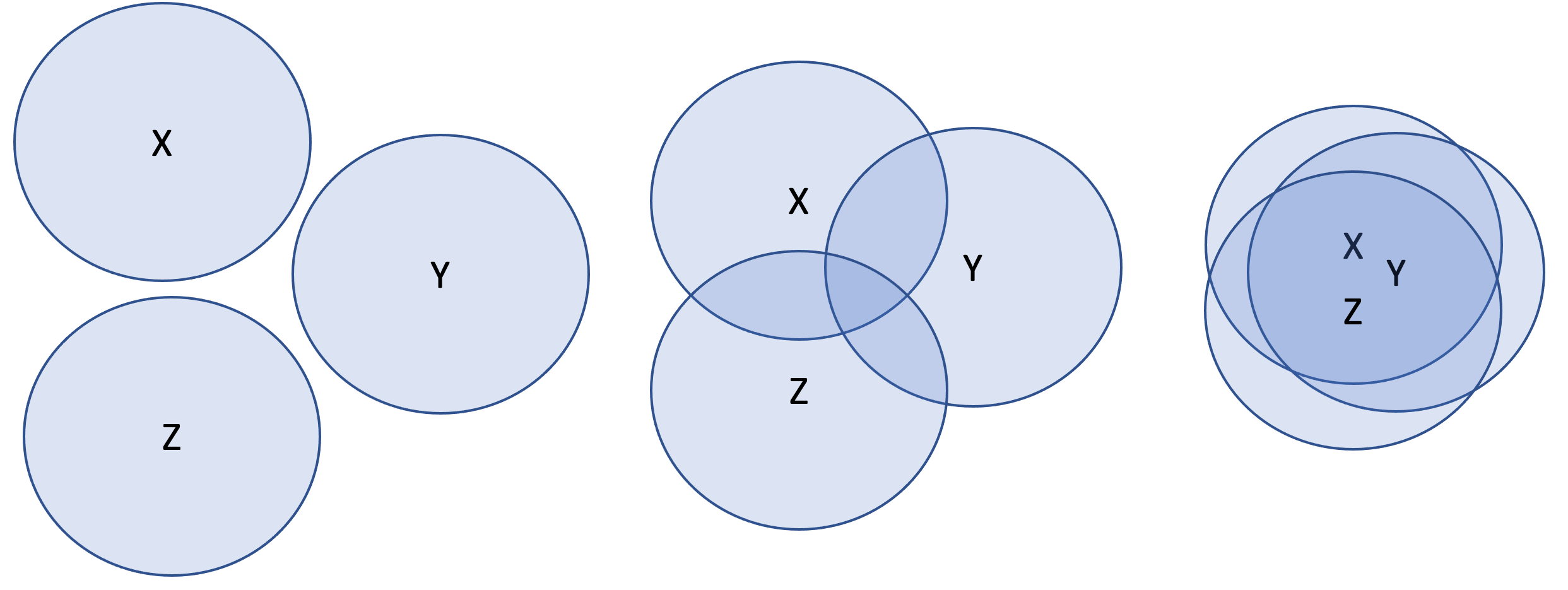
Abbildung: in Anlehnung an Tabachnick & Fidell (2007)
Diese zweite Abbildung weist auf unterschiedlich starke Korrelationen hin. Links in der Abbildung weisen die Varianzen der Variablen X, Z und Y keine Überschneidungsbereiche auf. Eine Korrelationsanalyse würde Koeffizienten von 0 ergeben. In der mittleren Darstellung weisen die Varianzen von X und Z und Z und Y sowie X und Y geringe Überschneidungen auf. Dies würde mit geringen Korrelationen einhergehen. In der rechten Darstellung sind diese Überschneidungsbereiche bzw. Korrelationen deutlich höher.
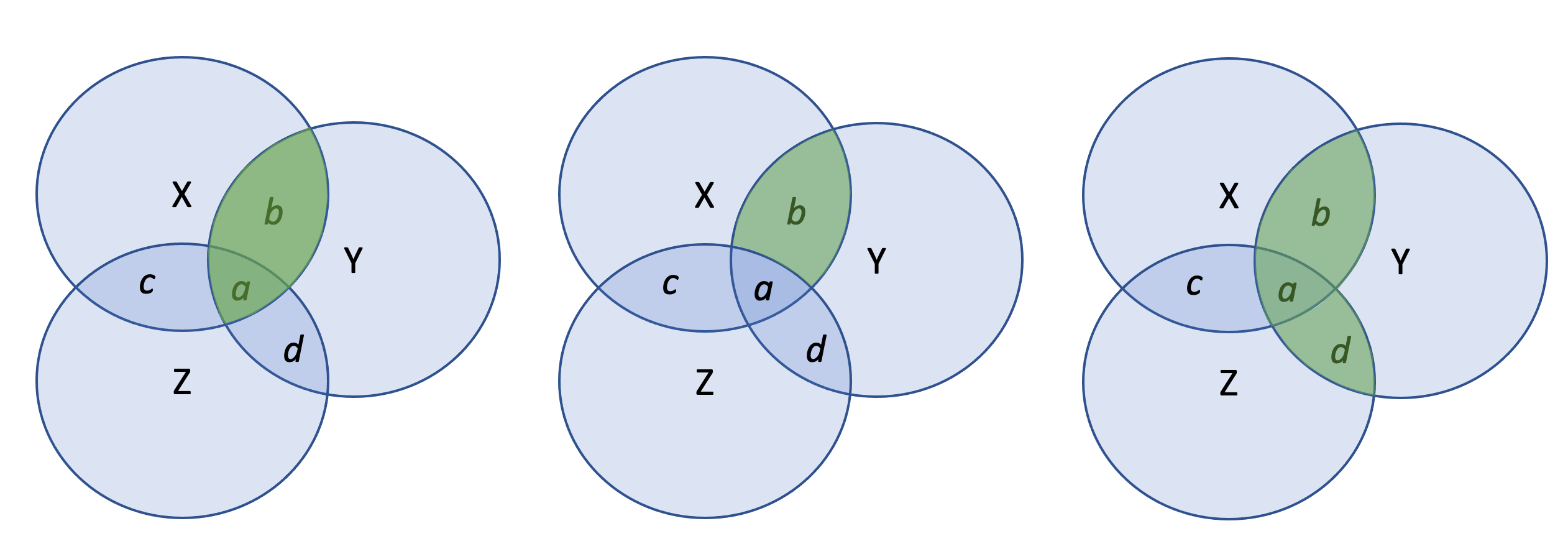
Die dritte Abbildung in Anlehnung an Tabachnick & Fidell (2007) zeigt unterschiedliche Korrelationstechniken auf, die mit unterschiedlichen Aussagen einhergehen. Das Ergebnis der bivariaten Korrelation von X und Y bezieht sich auf die gesamte Fläche in der sich die Varianz von X mit der Varianz von Y überschneidet (also die markierten Bereiche a und b). Dem entsprechend bezieht sich die bivariate Korrelation von X und Z auf die Bereiche c und a. Die bivariate Korrelation von Z und Y entspricht den Bereichen a und d.
Offensichtlich gibt es hier einen Bereich (a), der die Schnittmenge aller drei Varianzen repräsentiert.
Soll der partielle Zusammenhang von X und Y beschrieben werden, d.h. nur der Zusammenhang, der nicht auch durch andere Variablen (hier Z) beschrieben werden kann, resultiert die Partialkorrelation von X und Y aus dem Bereich b.
Die dritte Darstellung zeigt die multiple Korrelation von X, Z und Y auf, welche auch für das Verständnis der multiplen Regression bedeutsam ist. In der Regression entspricht der Wert des Determinationskoeffizienten R2 dem Teil der Varianz einer Variablen, der von dem Prädiktor (X) bestimmt wird (Wright, 1921).Sind die Werte eines Prädiktors konstant, verschwindet jeglicher prädiktiver Wert für Y, auch wenn Y variiert. Messen wir also eine unabhängige Variablen ohne Varianz, z.B. weil ein Item so formuliert ist, dass alle Befragten in gleicher Weise antworten, werden wir keinen Zusammenhang mit der abhängigen Variablen bestimmen können.
Am Rande sei hier angemerkt, dass eine solche Darstellung von Varianzen in vielen Fällen hilfreich sein kann. In dieser Abbildung wird in Anlehnung an Antonakis (2012) das Grundproblem der Endogenität dargestellt. Links abgebildet sehen Sie, dass die Variable ‘q’ eine gemeinsame Varianz mit X und mit Y aufweist. Wenn ‘q nicht in die Regressionsgleichung einbezogen werden würde, resultiert ein inkonsistenter Koeffizient für X mit Y, und X korreliert mit e. Mit anderen Worten, X würde verwendet um Y zu schätzen, aber Y enthält einen Varianzanteil bezeichnet mit ’e’, der auch in X enthalten ist, aber einen anderen (gemeinsamen) Ursprung hat.
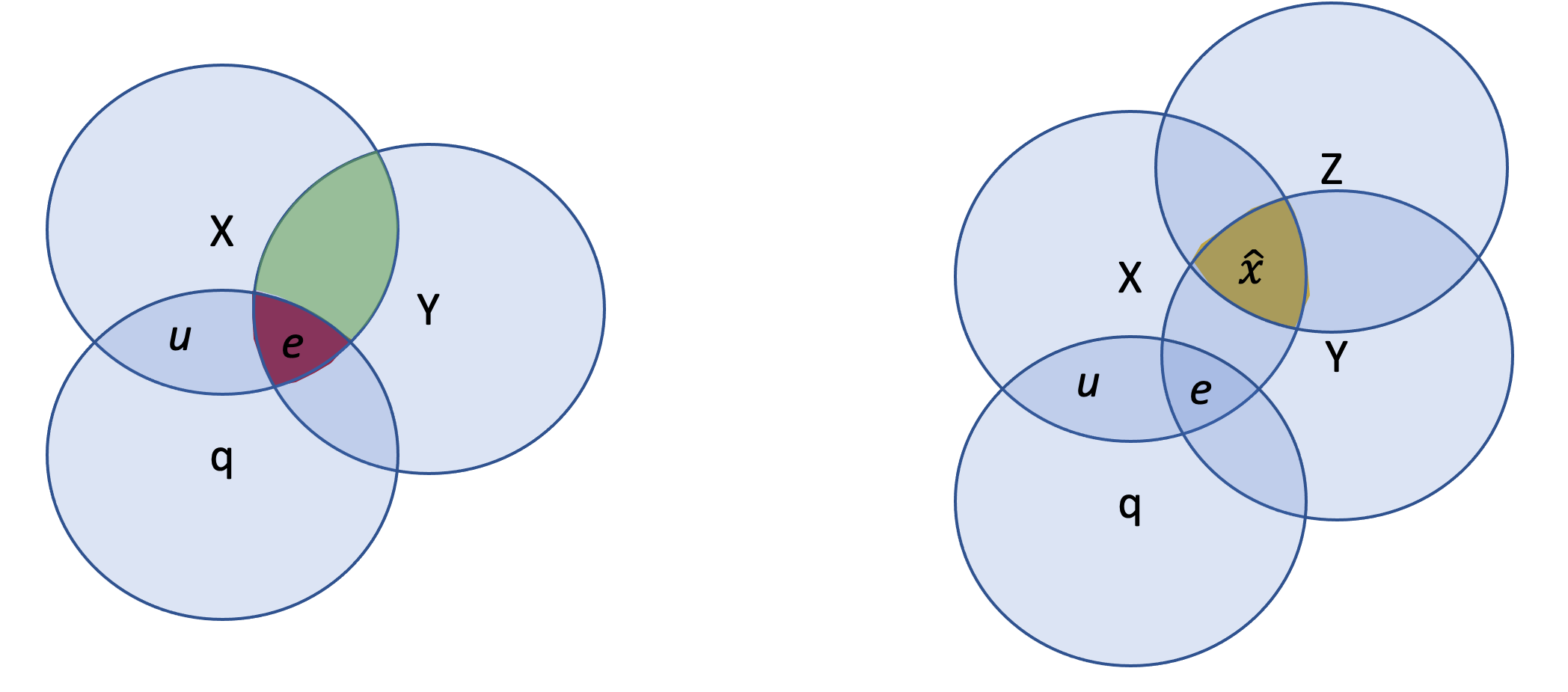
Abbildung: in Anlehnung an Antonakis (2012)
Rechts abgebildet ist die Darstellung mit einer zusätzlichen Instrumentalvariable, bezeichnet mit Z. Z teilt keine Varianz mit e. Nun wird der Anteil der Varianz, die X mit Z teilt verwendet, um den Zusammenhang mit Y zu bestimmen.
Diese als Two-stages least-squares (2SLS)-Ansatz bekannte Technik, ist die derzeit gängigste Lösung im Umgang mit dem Problem der Endogenität. Anders formuliert, anhand eines exogenen Instruments Z werden Schätzungen für X gemacht. Anhand dieser Schätzungen von X wird der Zusammenhang mit Y bestimmt. Der daraus resultierende Koeffizient weist dann einen konsistenten Wert auf.
2.2 Multiple Korrelationen
An dieser Stelle möchte ich zur Multiplen Korrelation zurückkehren. Wright (1921) erkannte, dass es häufig wünschenswert ist, Beziehungen gleichzeitig in einem System von mehr als zwei Variablen - in einer Matrix von Korrelationen - darzustellen. Die Möglichkeit der Matrixrepräsentation wurde durch Pearson (Wright, 1921) entwickelt. In dieser Matrix nimmt die Diagonale Werte von 1 an und die darüber liegenden Korrelationen zeigen die umgekehrte (man bezeichnet dies als transponierte) Form der darunter liegenden Korrelationen.
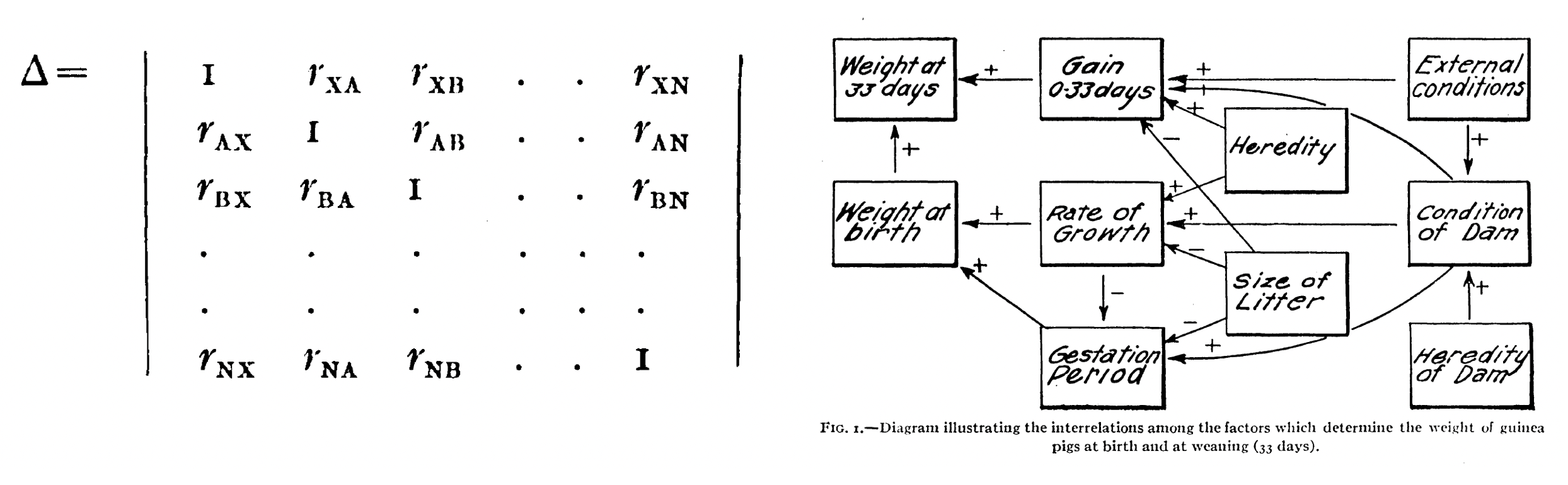
Quelle: Wright (1921) [558; 560]
Wright (1921) vermisste in allen vorhergehenden Ergebnisdarstellungen die Art der Beziehung (in Form der Richtung) zwischen den Variablen, wobei seiner Auffassung vorhandenes Wissen vernachlässigt würde (Wright, 1921). Daraus entwickelte sich seine Vorstellung, vorhandenes Wissen über die kausalen Zusammenhänge in die Wissensrepräsentation einzuschließen.
Seine Darstellung von der Gewichtszunahme von Meerschweinchen (Wright, 1921) gilt als erste Darstellung von Korrelationen in Form eines Pfadmodells. Die meisten Variablen sind miteinander durch mehr als einen Pfad verbunden. So korreliert das Gewicht bei der Geburt mit dem Gewicht nach 33 Tagen insgesamt als auch als Wirkung gemeinsamer Ursachen.
In seinem Beispiel führt eine hohe Fötenanzahl (‘size of letter’) zu einer kürzerer Tragezeit (‘gestation period’), aber dies wird wahrscheinlich dadurch ausgeglichen, das eine hohe Fötenanzahl auch die Wachstumsrate (‘rate of growth’) verringert. Langsameres Wachstum der Föten geht wiederum mit längerer Tragzeit einher.
Letztlich können sowohl ein schnelles Wachstum als auch eine längere Tragezeit zu hohem Geburtsgewicht führen (Wright, 1921). Während die bivariate Korrelationen zweier Variablen als Resultat aller damit verbundenen Variablen zu sehen sind, geben die Partialkorrelationen den ‘direkten’ Effekt unter der Annahme, dass die anderen Variablen konstant sind, wieder.
Die Interpretation von Pfadkoeffizienten in Bezug auf den Anteil der Varianz, die durch eine Variable erklärt wird, wurde erst später weiterentwickelt, unterscheidet sich aber in einfachen Modellen nicht (Pearl & Mackenzie, 2018, S. 77).
2.3 Pfadmodell
Das heutige Verständnis betrachtet Pfadmodelle im Allgemeinen als “eine Regressionsanalyse, in welcher simultan mehrere abhängige Variablen betrachtet werden” (Geiser, 2011, S. 75). Exogene Variablen also die unabhängigen Variablen eines Pfadmodells können untereinander korrelieren.3
An dieser Stelle möchte ich auf zwei zentrale Konzepte der Pfadmodellierung eingehen. Das erste Konzept bezieht sich auf die Positionierung der Variablen im Modell. Das zweite Konzept bezieht sich auf die Effektzerlegung im Modell.
“Variablen, die im Modell durch eine oder mehrere andere Variablen vorhergesagt werden, nennt man endogene Variablen” (Geiser, 2010, S. 41). Links in folgender Abbildung ist ein Modell mit drei Variablen A, B und C dargestellt. A wird zur Prognose von B und C verwendet. Zudem wird B als Prädiktor für C angesehen. Die Annahmen der Wirkungszusammenhänge in diesem Modell repräsentiert insofern die Darstellung einer traditionellen Mediationsanalyse nach Baron & Kenny (1986, S. 1176).
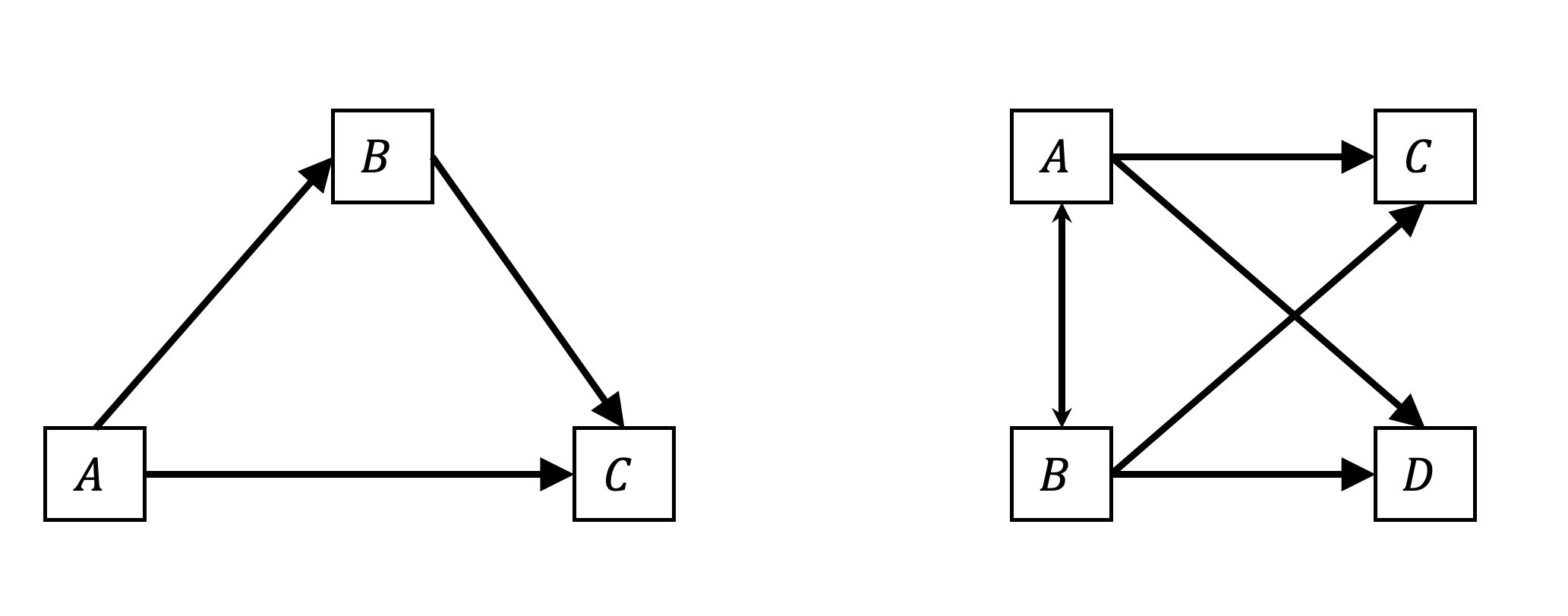Anmerkung: In der Mathematik speziell in der Algebra werden die Kleinbuchstaben a, b, c für bekannte Größen und x, y, z für unbekannte Größen verwendet. Diese Notation wird häufig der Festlegung durch Descartes (1637) in ‘La Géométrie’ zugeschrieben. In dieser Abbildung stehen die Großbuchstaben A, B, C, D für Variablen.
Damit weist das linke Modell zwei endogene Variablen (B und C) auf. Modellvariablen, die nicht endogen sind, werden als exogene Variablen bezeichnet. Das diese Variablen als exogen bezeichnet werden, schließt allerding nicht aus, dass es unberücksichtigte Variablen gibt, die einen Einfluss auf diese Variablen haben könnten.
Erinnern wir uns zurück an die Prozedur eines Mediatornachweises. Zu Grunde liegt ein signifikanter Zusammenhang zwischen der unabhängigen Variable (A) und der abhängigen Variable (C). Um zu überprüfen, ob die Variable B ein geeigneter Mediator ist, der den Zusammenhang zwischen A und C erklären kann, werden drei Analyseschritte durchgeführt.
Zuerst wird der Zusammenhang zwischen der unabhängigen Variablen (A) und dem potenziellen Mediator (B) bestimmt. Ein signifikanter Regressionskoeffizient wird vorausgesetzt.
Im zweiten Schritt wird der Zusammenhang zwischen dem potenziellen Mediator (hier B) und der abhängigen Variablen (C) bestimmt. Auch hier wird ein signifikanter Regressionskoeffizient vorausgesetzt. Im dritten Schritt wird die abhängige Variable C in einer multiplen Regression durch A und B bestimmt.
Die Variable B kann dann als Mediator für den Zusammenhang von A und C angesehen werden, wenn sich in der multiplen Regression der Regressionskoeffizient der Variablen B als signifikant bestätigt und sich die vormals signifikante Beziehung von A auf C als nicht mehr signifikant darstellt.
Rechts in der Abbildung ist ein Modell mit vier Variablen dargestellt. A und B sind exogene Variablen. C und D sind endogene Variablen. Dieses relativ einfache Modell kann in dieser Form nicht durch einzelne Regressionen ersetzt werden.
2.3.1 Exogene vs. endogene Variablen
Die Unterscheidung zwischen exogenen und endogenen Variablen in Pfadmodellen ist essentiell. Im Pfadmodell werden die Pfadkoeffizienten von exogenen auf endogene Variablen mit gamma (\(\gamma\)) und Pfadkoeffizienten von endogenen auf endogene Variablen mit beta (\(\beta\)) bezeichnet (vgl. z.B. LISREL Terminologie) (Gefen, Straub & Marie-Claude, 2000, S. 22). Alle endogenen Variablen weisen einen Residual-Term zeta (\(\zeta\)) auf (manchmal auch als Störterm bzw. disturbances term bezeichnet), der alle Einflüsse auf die endogenen Variablen darstellt, die nicht durch das Modell erklärt werden. Des Weiteren werden Kovarianzen zwischen exogenen Variablen mit Phi (\(\Phi\)) und Kovarianzen zwischen den Störungstermen der endogenen Variablen mit Psi (\(\Psi\)) bezeichnet.
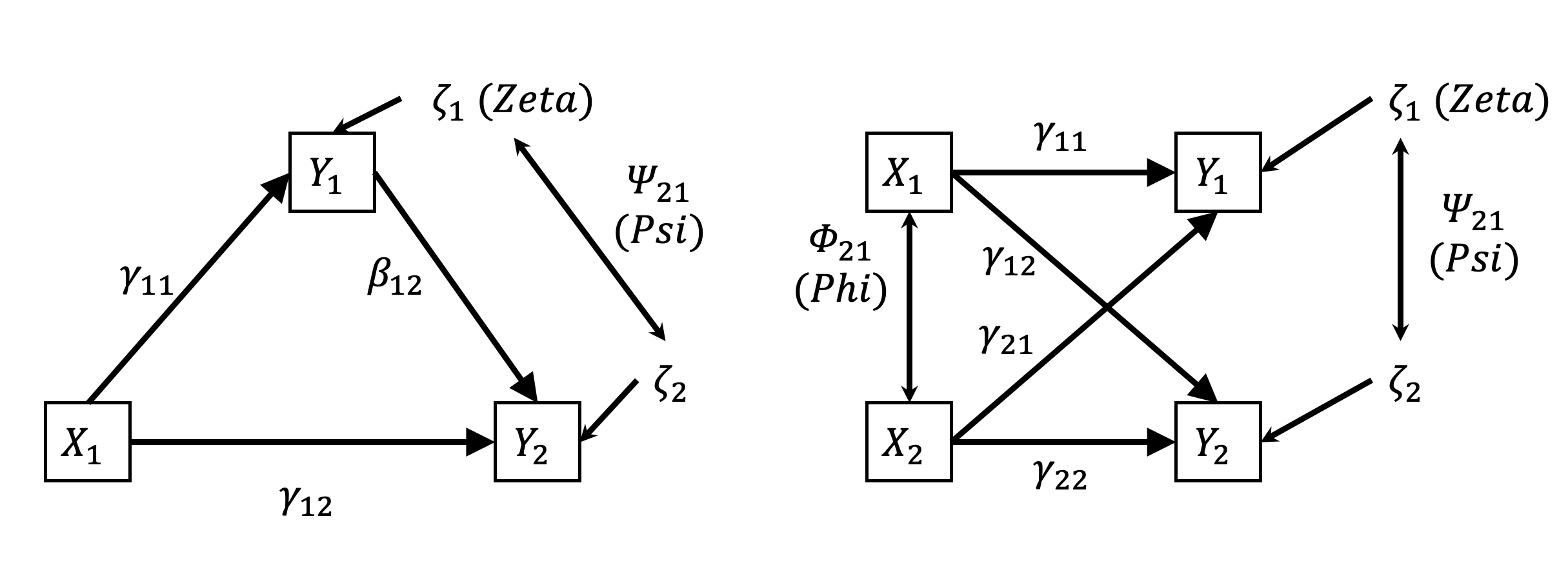Anmerkung: Die Bezeichnungen X und Y wurden hier gewählt, um darzulegen, dass X als exogen und Y als endogen angesehen wird.
2.3.2 Effektzerlegung
Das zweite Konzept der Pfadmodellierung, auf das ich zu sprechen kommen möchte, ist das Konzept der Effektzerlegung.
In dem links dargestellten Mediationsmodell entspricht der direkte Effekt (DE) von X1 auf Y2 dem Pfadkoeffizienten \(\gamma\)12.
\[DE=\gamma_{12}\] Dieser Pfadkoeffizient gibt an, zu welchem Anteil und mit welcher Richtung (also positiv oder negativ) die Variable X1 auf Y2 wirkt, wenn simultan berücksichtigt wird, dass auch Y1 auf Y2 wirkt.
Der indirekte Effekt (IE) von X1 auf Y2 ergibt sich aus dem Produkt der Pfadkoeffizienten \(\gamma\)_11 und \(\beta\)_12. Der indirekte Effekt weist darauf hin, in welcher Weise die Variable X1 über den Mediator Y1 auf die Variable Y2 wirkt.
\[IE=\gamma_{11}\beta_{12}\] Letztendlich ergibt sich der totale Effekt (TE) von X1 auf Y2 aus der Summe des direkten und des indirekten Effektes (Muthén & Asparouhov, 2015). Dieser Effekt zeigt somit auf, wie die Variable Y2 direkt durch X1 und indirekt über den Mediator Y1 erklärt werden kann.
\[TE=DE+IE=\gamma_{12}+\gamma_{11}\beta_{12}\] Im rechts dargestellten Modell liegt keine Mediation vor. In diesem Fall ergibt sich Y1 als Summe der Produkte der Pfadkoeffizienten mit den Werten der entsprechenden exogenen Variablen und dem nicht durch das Modell erklärte Residuum ζ.
\[Y_1=\gamma_{11}X_1+\gamma_{21}X_2+\zeta_{1}\] \[Y_2=\gamma_{12}X_1+\gamma_{22}X_2+\zeta_{2}\]
2.3.3 Interaktion
Während wir bislang aufgezeigt haben, wie sich der Regressionskoeffizient einer Variablen X, also der direkte Effekt einer Variablen X auf eine Variablen Y) unter simultaner Betrachtung weiterer Variablen (z.B. eines Mediators) verändert, möchte ich im Folgenden auf das Konzept der Moderation eingehen. “Ein Moderatoreffekt [liegt] dann vor, wenn eine Interaktion zwischen zwei Variablen besteht. Eine Variable wird als Moderatorvariable bezeichnet, wenn sie die Stärke des direkten Einflusses einer Variable auf ein Kriterium beeinflusst.” (Geiser, 2011, S. 77).
Dies entspricht der allgemeinen Definition eines Moderators von (Baron & Kenny, 1986, S. 1174), wonach ein Moderator eine Variable darstellt, der die Richtung oder Stärke des Zusammenhanges zwischen einer unabhängigen Variablen und einer abhängigen Variablen bestimmt:
„In general terms, a moderator is a […] variable that effects the direction and/ or strenght of the relation between an independent or predictor variable and a dependent or criterion variable“ (Baron & Kenny, 1986, S. 1174).
Für metrische Variablen schlagen sie einen analytischen Test vor, der den Produktterm der unabhängigen Variablen und des Moderators einbezieht. Da analytisch nicht zwischen unabhängiger Variable und Moderator zu unterscheiden ist und die Zuweisung von unabhängiger Variable bzw. Moderator rein theoretisch herzuleiten ist (Baron & Kenny, 1986, S. 1174), wird die Moderationsanalyse häufig auch als Interaktionsanalyse bezeichnet (Berry, Golder & Milton, 2012).
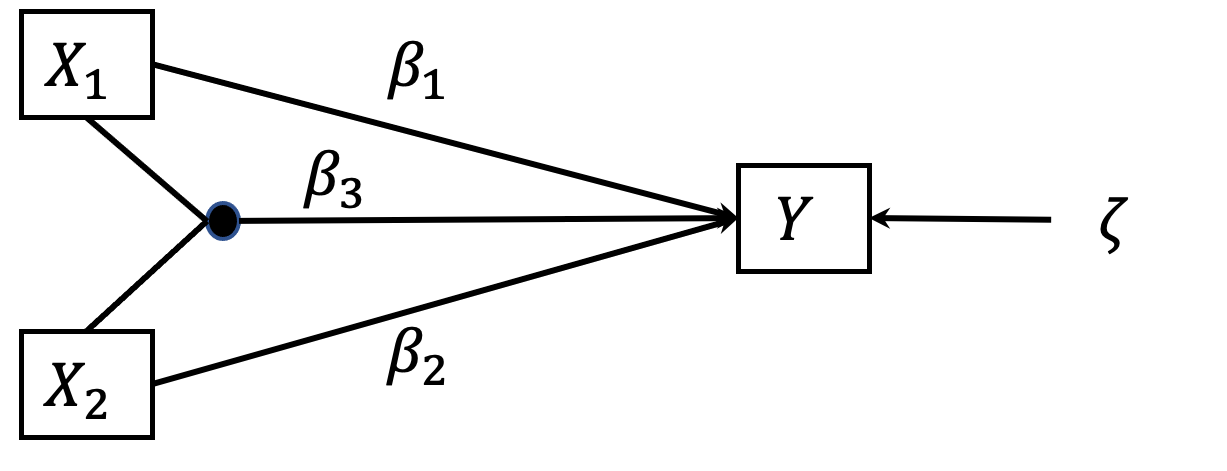
Dawson (2014) argumentiert, dass die Werte der interagierenden Variablen vor der Bildung des Produktterms standardisiert oder zumindest zentriert werden. Besondere Beachtung sollte dabei auf hohe Korrelationen zwischen der interagierenden Variablen gerichtet werden. Bei Korrelationen zwischen 0.3 und 0.5 wird von Dawson (2014) die zusätzliche Einbeziehung quadratischer Terme empfohlen, bei Korrelationen >0.5 sollten sie nicht unberücksichtigt bleiben Dawson (2014).
Die Bildung quadratischer Terme (nichtlineare Terme) erfolgt durch quadrieren der Werte einer Variablen. In Erweiterung zu diesem Vorgehen können auch Mehrfachinteraktionen (z. B. Interaktionen zwischen drei Variablen) operationalisiert werden (Dawson & Richter, 2006).
Während Mediatoren im Pfadmodell als endogene Variablen angesehen werden, werden Moderatoren als exogene Variablen angesehen (Baron & Kenny, 1986, S. 1174).
Die Interpretation des Interaktionsterms einer unabhängigen Variable mit einem Moderator bezeichnet insofern nicht den Effekt einer Ursache (‘effect of cause’), sondern die Ursache eines Effektes (‘cause of effect’) (Pearl, 2015).
Dies wird in der folgenden Darstellung verdeutlicht, erfordert allerdings eine theoretische Argumentation, warum gerade X2 als Moderator des Effektes von X1 auf Y angesehen wird und nicht X1 als Moderator des Effektes von X2 auf Y.
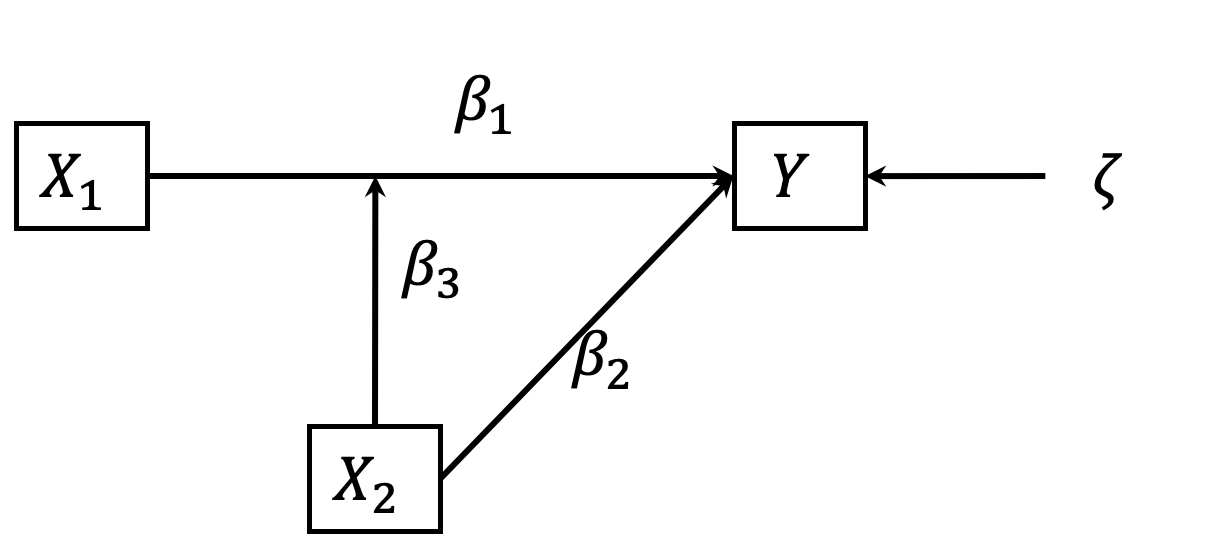
Wenn aus einer Interaktionsanalyse ein signifikanter Koeffizient für den Interaktionsterm resultiert, werden die Ergebnisse typischerweise in Interaktionsplots dargestellt. Dabei werden die Prognosen der abhängigen Variablen (hier Verständnis) als Resultat der Schätzgleichung für verschiedene Ausprägungen der interagierenden Variablen dargestellt.
\[ Y=\beta_0 + \beta_1X_1 + \beta_2X_2+\beta_3X_1X_2+\zeta \]
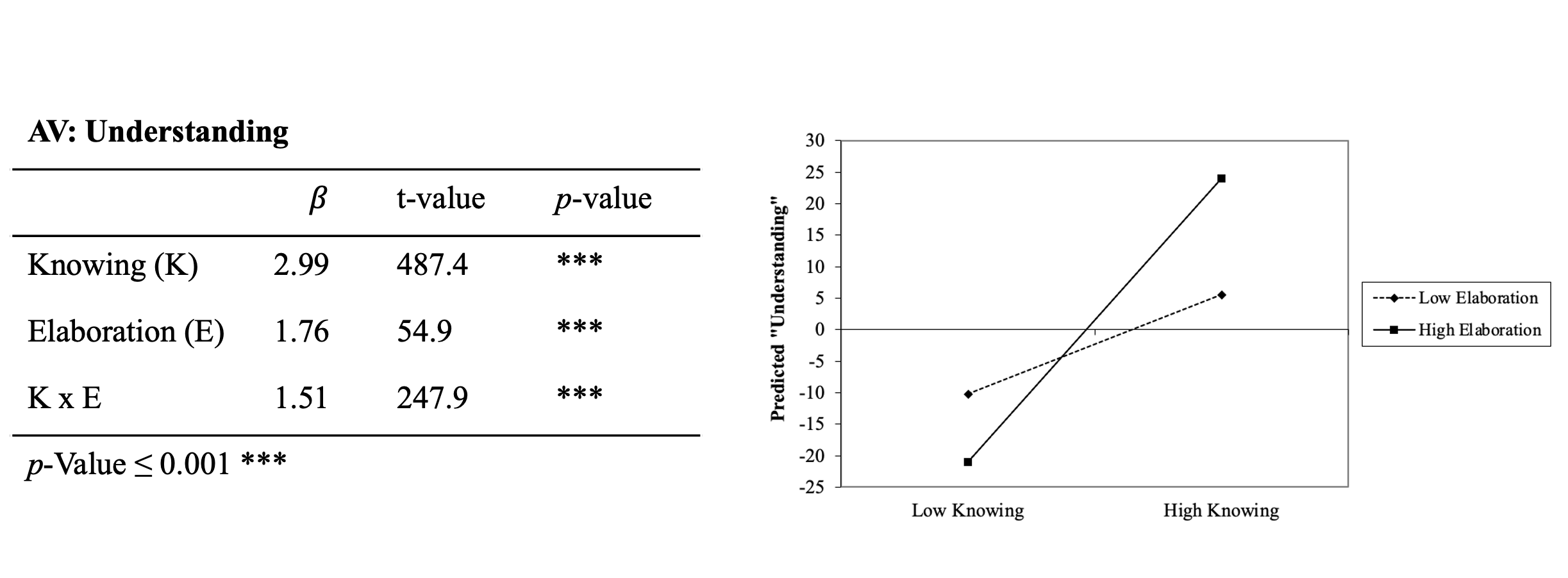
Für den Fall, dass geringes Lernen mit geringer Vertiefung einher geht, resultiert ein Wert von etwa -10 für Verständnis. Bei gleichbleibend geringer Vertiefung steigt der prognostizierte Wert für Verständnis mit zunehmendem Wissen an und erreicht einen Wert von etwa +5. Liegt eine hohe Vertiefung von Wissen vor, wird ein deutlich höherer Anstieg im prognostizierten Verständnis deutlich (von -20 auf +25).
Das Niveau der abhängigen Variablen bildet insofern das gemeinsame Resultat von Lernen, Vertiefung und der Interaktion von Lernen und Vertiefung ab.
Häufig sind Hypothesen nicht hinsichtlich einer Interaktion formuliert (hier ‘Wissen und Vertiefung interagieren positiv auf das Verständnis’) sondern sind auf klare Zuordnung von unabhängiger Variable und Moderator ausgerichtet (hier ‘Der positiver Einfluss von Wissen auf das Verständnis wird durch hohe Elaboration verstärkt’). Diese Formulierung bezeichnet eine konditional abhängige Beziehung zwischen Wissen und Verständnis durch Elaboration.
Dabei wird der Einfluss der unabhängigen Variable auf die abhängige Variablen als partielles Differential der Funktion mit Interaktionsterm abgeleitet (Berry et al., 2012; Brambor, Clark & Golder, 2006) als:
\[ \frac {\partial Y}{\partial X_1} = \beta_1 +\beta_3X_2 \]
Die resultierende Funktion liefert somit den tatsächlichen Effekt von X1 auf Y bei unterschiedlichen Ausprägungen des Moderators X2 (ohne den Effekt des Moderators auf die AV). Insofern kann tatsächlich eine Aussage über die Veränderung eines Effektes durch eine zweite Variable getroffen werden.
Eine weitere Besonderheit der Pfadmodellierung ist die Möglichkeit der Bestimmung von Nicht-rekursiven Modellen. Dazu werden jedoch weitere Daten in Form von Instrumenten vorausgesetzt.
2.4 Erste Anwendungen mit dem R-package ‘lavaan’
Im ersten Vortragsteil hatte ich ein bisschen über die Gefahr von falschen Schlüssen durch Ergebnisse, die aus falschen Fragestellungen oder Interpretation resultieren, berichtet
Im Anschluss habe ich die Varianz von Variablen als mengentheoretische Darstellung im VENN-Diagramm vorgestellt und die Schnittmenge der Varianzen zweier Variablen im Sinne von bivariaten Korrelationen dargestellt. Ich bin auf die Bedeutung von bivariaten Schnittmengen eingegangen, wenn diese zusätzlich Schnittmengen mit dritten Variablen aufweisen.
Ausgehend von multivariate Korrelationsmatrizen habe ich ihre Darstellung als Pfadmodell vorgestellt.
Dabei wurden endogene Variablen von exogenen Variablen entsprechend ihrer Position im Modell unterschieden.
Als zweites zentrales Konzept habe ich die Effektzerlegung vorgestellt. Dabei habe ich erklärt, dass sich der Totale Effekt einer exogenen Variable auf eine endogene Variable unter Einbeziehung eines Mediators als Summe des direkten und des indirekten Effektes ergibt, wobei sich der indirekte Effekt aus dem Produkt des Pfadkoeffizienten der unabhängigen Variable auf den Mediator und dem Pfadkoeffizienten des Mediators auf die abhängige Variable ergibt.
Zuletzt habe ich die Moderation als spezifische Form der Interaktion dargestellt und den Unterschied zwischen einem signifikanten Interaktionsterm und dem marginalen Effekt der unabhängigen Variable bei verschiedenen Ausprägungen eines Moderators vorgestellt.
Das waren relativ viele Informationen und so werde ich die beiden letzten Konzepte hier noch einmal anhand von Datenbeispielen aufgreifen.
Dabei verwende ich bereits die Programm-Bibliothek ‘Lavaan’ (Rosseel, 2012) in der Statistikumgebung ‘R’ (R Core Team, 2021), auf deren Installation ich hier aber nicht weiter eingehe. Mit ‘Lavaan’ können komplexe Strukturgleichungsmodelle bestimmt werden, zuerst jedoch ein einfaches Pfadmodell.
Zuerst soll das bereits besprochene Mediationsmodell von Lernen, Wissen und Verständnis überprüft werden. Wir möchten also an dieser Stelle die Hypothesen überprüfen, dass ‘Lernen das Verständnis fördert’ und das ‘Wissen den Zusammenhang zwischen Lernen und Verständnis’ erklärt, also ein Mediator bzw. eine intervenierende Variable für diesen Zusammenhang darstellt.
set.seed(1896) # dieser Wert dient der Reproduzierbarkeit
# von Stichproben aus Zufallszahlen
n <- 1000 # Festlegung der Größe des Samples
# normalverteilte Zufallswerte für Lernen werden bestimmt
learning <- rnorm(n)
# Wissen wird aus Lernen bestimmt
knowing <- 5 * learning + rnorm(n)
# Verständnis wird aus Wissen bestimmt
understanding <- 3 * knowing + rnorm(n)plot(learning, understanding)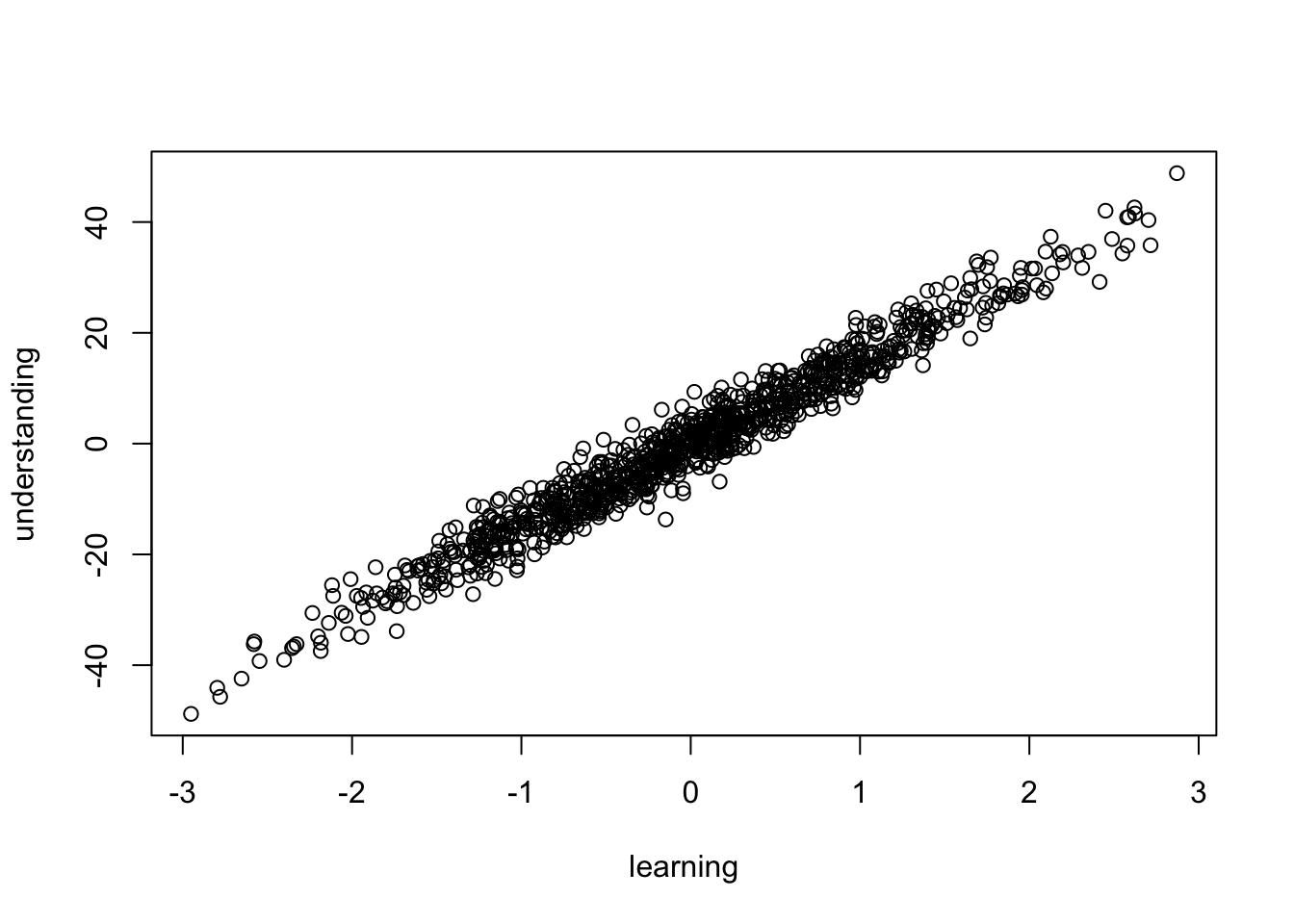
Der Plot weist auf einen linearen Trend hin, dass mit steigendem Lernen ein stetig steigendes Verständnis einhergeht.
plot(knowing, understanding)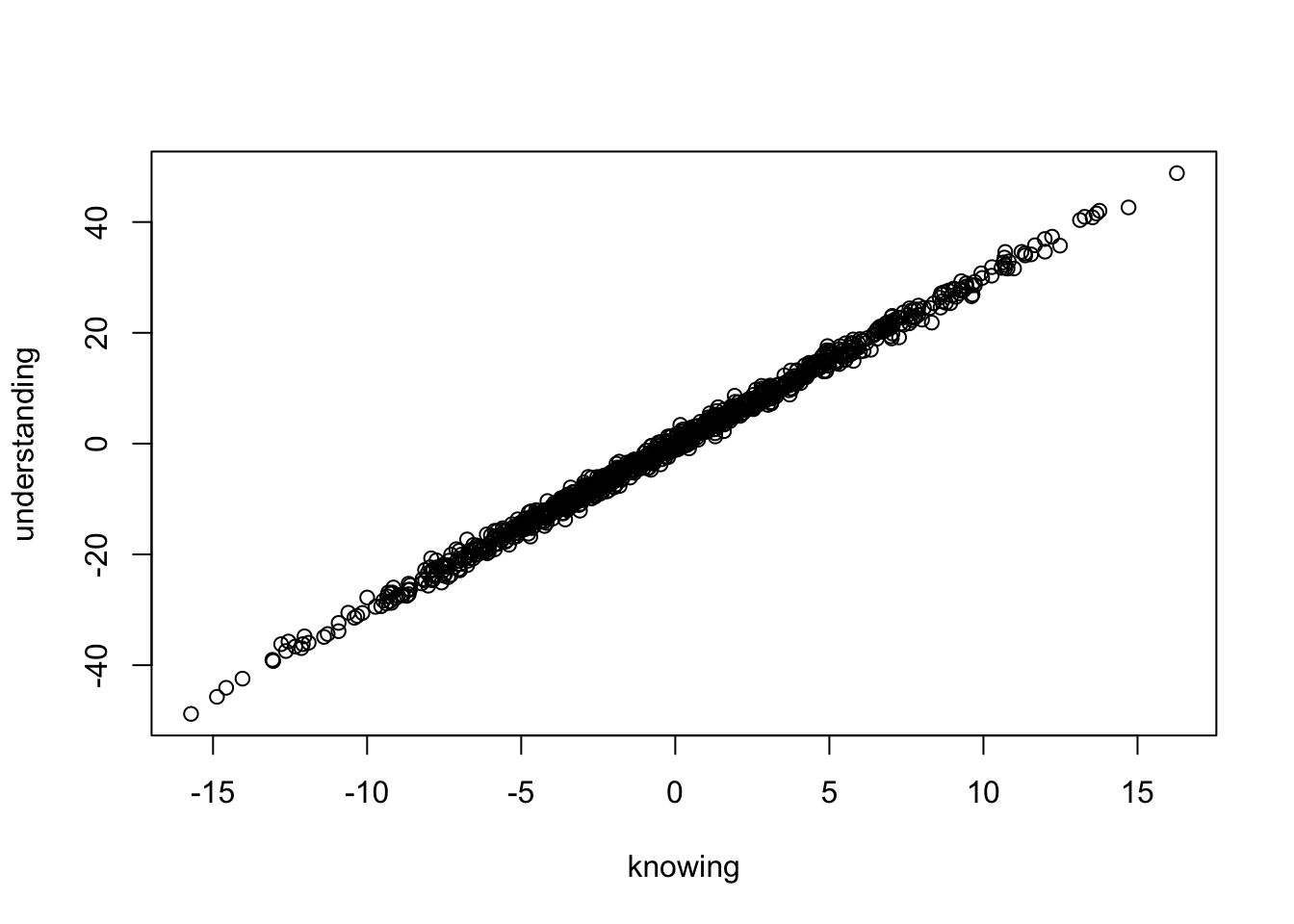
Auch diese Abbildung weist einen linearen Trend auf. Mit steigendem Wissen geht ein stetig steigendes Verständnis einher.
mediation_data <- data.frame(cbind(learning, knowing, understanding))
head(mediation_data)## learning knowing understanding
## 1 2.03365024 10.993847506 31.61270171
## 2 0.13466066 -0.151545780 0.24854481
## 3 0.59787859 3.779447005 11.89693448
## 4 0.06392520 0.002531287 -0.03264364
## 5 0.21673542 2.587983621 6.78699155
## 6 0.03408985 0.476003332 1.01233456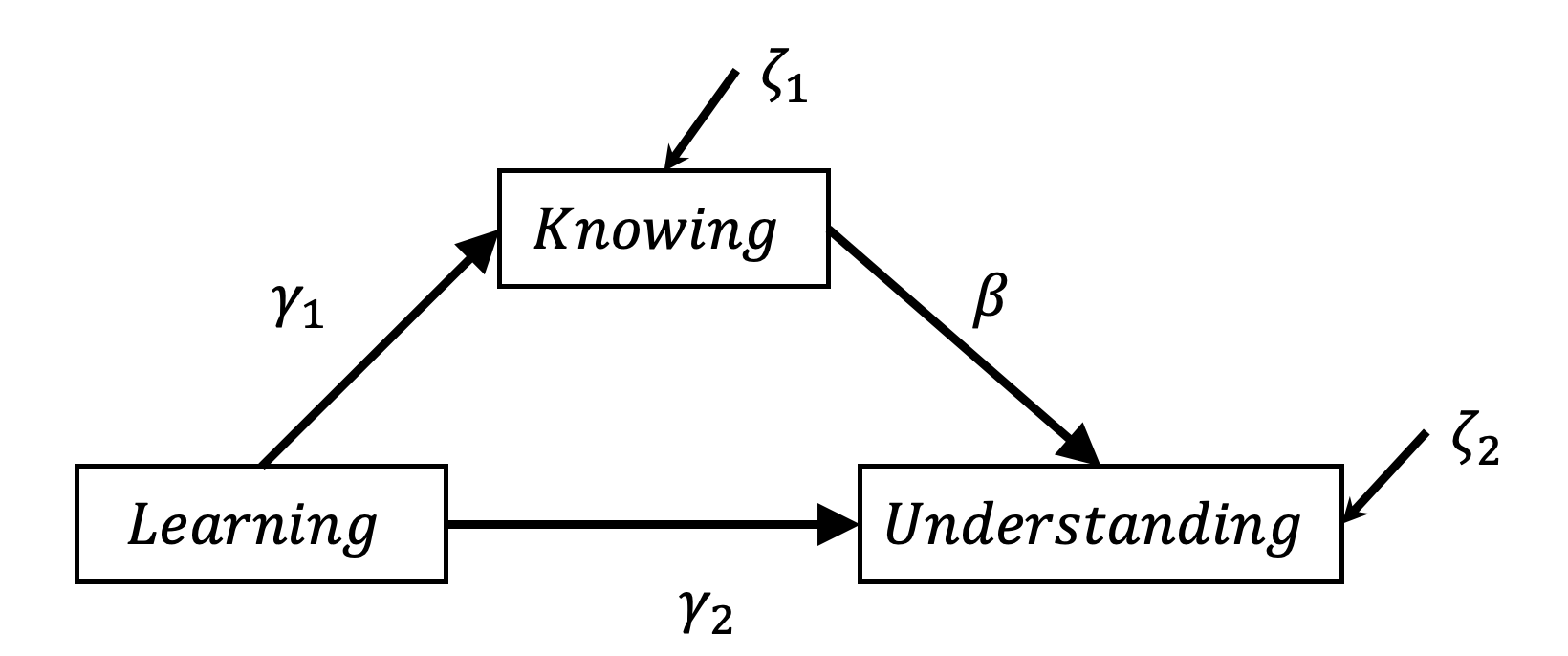
Dargestellt sind die hypothetischen Zusammenhänge zwischen Lernen, Wissen und Verständnis gemaß der Hypothesen H1: Lernen fördert Verständnis und H2: Durch höheres Wissen wirkt das Lernen positiv auf das Verständnis.
Das zu bestimmende Modell beinhaltet die drei Pfadkoeffizienten \(\gamma\)1, \(\gamma\)2 und \(\beta\). Anhand welcher Koeffizienten wird über diese Hypothesen entschieden?
Die erste Hypothese wird unterstützt, wenn sich der totale Effekt von Lernen auf Verständnis signifikant unterschiedlich von Null darstellt.
Der totale Effekt ergibt sich aus der Summe des direkten Effektes und dem Produkt der Pfadkoeffizienten des indirekten Effektes, also in diesem Fall:
\[
TE= \gamma_2+\gamma_1 \beta
\]
Über die zweite Hypothese würde anhand des indirekten Effektes entschieden, also in diesem Fall:
\[
IE= (\gamma_1 \beta)
\]
2.4.1 Beispiel: Indirekte Effekte/ Mediation
Erinnern wir uns zurück, um diese Zusammenhänge mittels Regression zu prüfen, hätten wir drei einfache Regressionen zu berechnen. In “Lavaan” definieren wir lediglich ein Modell, dass drei Regressionen enthält.
library (lavaan)## This is lavaan 0.6-10
## lavaan is FREE software! Please report any bugs.Die zugrunde liegenden Daten habe ich in der Datenmatrix ‘mediation_data’ vorliegen. Dabei handelt es sich um 1000 Fälle aus einer Simulation. Die hier gezeigten Schritte können ausprobiert werden. Die entsprechende R-Syntax stelle ich im Skript zum Vortrag zur Verfügung.
Wir bezeichnen das Modell mit den Namen ‘model1’ und weisen ihm die Variablen und die zu berücksichtigenden Zusammenhänge zwischen den Variablen zu. Anfang und Ende der Modelldefinition werden mit Hochkommata aufgezeigt. Regressionspfade werden wie bei allen Regressionsmodellen in ‘R’ mit einer ‘Tilde’ definiert.
model1 <-
'understanding ~ learning
understanding ~ knowing
knowing ~ learning
'Im zweiten Schritt verwenden die Anweisung ‘SEM’ zur Modellprüfung und weisen dieser Funktion das definierte Modell und den Namen der Datenmatrix, in der sich die Daten befinden, zu.
model1_FIT <- sem(model1,data=mediation_data)Das Ergebnis der Modellprüfung wird hier unter der Bezeichnung ‘model1_FIT’ gespeichert. Die Anzeige des Ergebnisses erfolgt mittels der Anweisung ‘summary’.
summary(model1_FIT)## lavaan 0.6-10 ended normally after 24 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 1000
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## understanding ~
## learning 0.122 0.162 0.749 0.454
## knowing 2.982 0.032 94.168 0.000
## knowing ~
## learning 5.030 0.031 161.920 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .understanding 0.943 0.042 22.361 0.000
## .knowing 0.941 0.042 22.361 0.000Übertragen wir diese Werte in unsere Abbildung bekommen wir folgende Darstellung. Hier sind auch bereitsder totale und der indirekte Effekt aufgeführt.
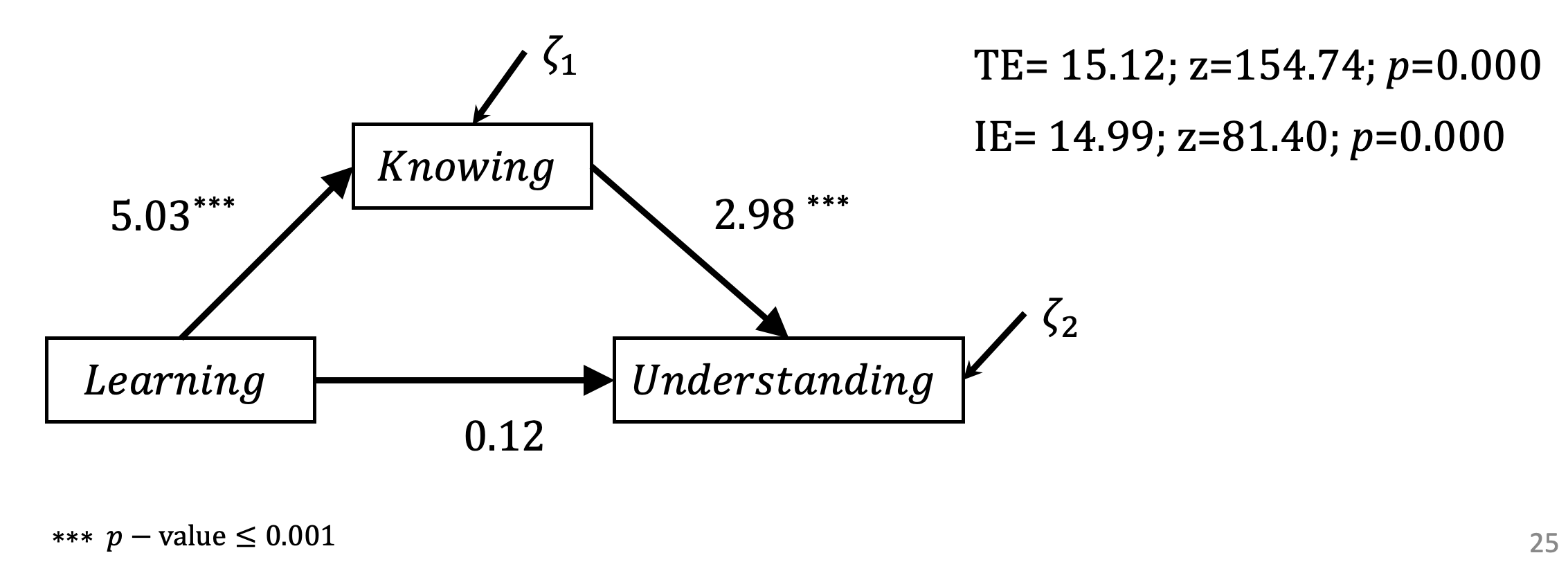
Um den totalen und den indirekten Effekt auf Signifikanz zu überprüfen, definieren wir in der Syntax sogenannte Label für die zu schätzenden Parameter (gamma1, gamma2 und beta) und definieren anhand dieser Label die gesuchten totalen und indirekten Effekte. Zur Definition werden hier ‘Doppelpunkt und Gleichheitszeichen’ verwendet.
model1 <-
'understanding ~ gamma2*learning
understanding ~ beta*knowing
knowing ~ gamma1*learning
TE := gamma2 + (gamma1*beta)
IE := gamma1*beta
'Wir starten die Modellprüfung wieder mit der Anweisung ‘sem’ und erhalten das Ergebnis mit der Anweisung ‘summary’.
model1_FIT <- sem(model1,data=mediation_data)
summary(model1_FIT)## lavaan 0.6-10 ended normally after 24 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 1000
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## understanding ~
## learnng (gmm2) 0.122 0.162 0.749 0.454
## knowing (beta) 2.982 0.032 94.168 0.000
## knowing ~
## learnng (gmm1) 5.030 0.031 161.920 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .understanding 0.943 0.042 22.361 0.000
## .knowing 0.941 0.042 22.361 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## TE 15.121 0.098 154.740 0.000
## IE 14.999 0.184 81.403 0.000In diesem Fall würde sich ein totaler Effekt von TE=15.12; z=154.74; p \(\leq\) 0.000 ergeben, so dass die Hypothese 1 angenommen werden könnte. Der signifikante indirekte Effekt (IE= 14.99; z=81.40; p \(\leq\) 0.000) unterstützt die Hypothese 2.
Siehe auch https://lavaan.ugent.be/tutorial/means.html
Anmerkung: Am Rande möchte ich hier anmerken, dass wir aufgrund der Datengenerierung durch Simulation wissen, dass Verständnis in diesem Beispiel nicht direkt durch Lernen (learning) determiniert wurde, sondern allein durch Wissen (knowing).
Trotzdem wird dieser Zusammenhang vorgefunden und bestätigt. Genau genommen besteht die Abhängigkeit zwischen Lernen und Verständnis hier also konditional durch die Variable Wissen.
Würde hier ein Modell ohne die Variable Wissen berechnet werden, würde - wie im folgenden Beispiel gezeigt - ein signifikant positiver Zusammenhang zwischen Lernen und Verständnis auftreten, der in den Daten gar nicht determiniert wurde.
model1 <-
'understanding ~ learning'
model1_FIT <- sem(model1,data=mediation_data)
summary(model1_FIT)## lavaan 0.6-10 ended normally after 1 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 2
##
## Number of observations 1000
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## understanding ~
## learning 15.121 0.098 154.740 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .understanding 9.309 0.416 22.361 0.0002.4.2 Beispiel: Interaktion/ Moderation
Nun soll das bereits besprochene Moderationsmodell von Wissen, Elaboration und Verständnis in ein Pfadmodell übertragen werden. Wir möchten an dieser Stelle die Hypothesen überprüfen, dass “Wissen und Elaboration hinsichtlich des Verständnisses interagieren” und das “der positive Einfluss von Wissen auf das Verständnis durch hohe Elaboration verstärkt wird”, also das Elaboration ein Moderator für den Zusammenhang zwischen Wissen und Verständnis darstellt.
#Erstellen von Simulationsdaten für Moderation
# Dieser Wert dient der Reproduzierbarkeit von
# Stichproben aus Zufallszahlen
set.seed(1896)
# Festlegung der Größe des Samples
n <- 1000
# normalverteilte Zufallswerte für Lernen werden bestimmt
learning <- rnorm(n)
# Wissen wird aus Lernen bestimmt
knowing <- 5 * learning + rnorm(n)
# Wissensvertiefung ist unabhängig vom Wissen
elaboration <- rnorm(n)
# Verständnis wird aus Wissen bestimmt
understanding <- 3 * knowing + 2*elaboration +
(1.5*knowing*elaboration) + rnorm(n)plot (knowing, understanding)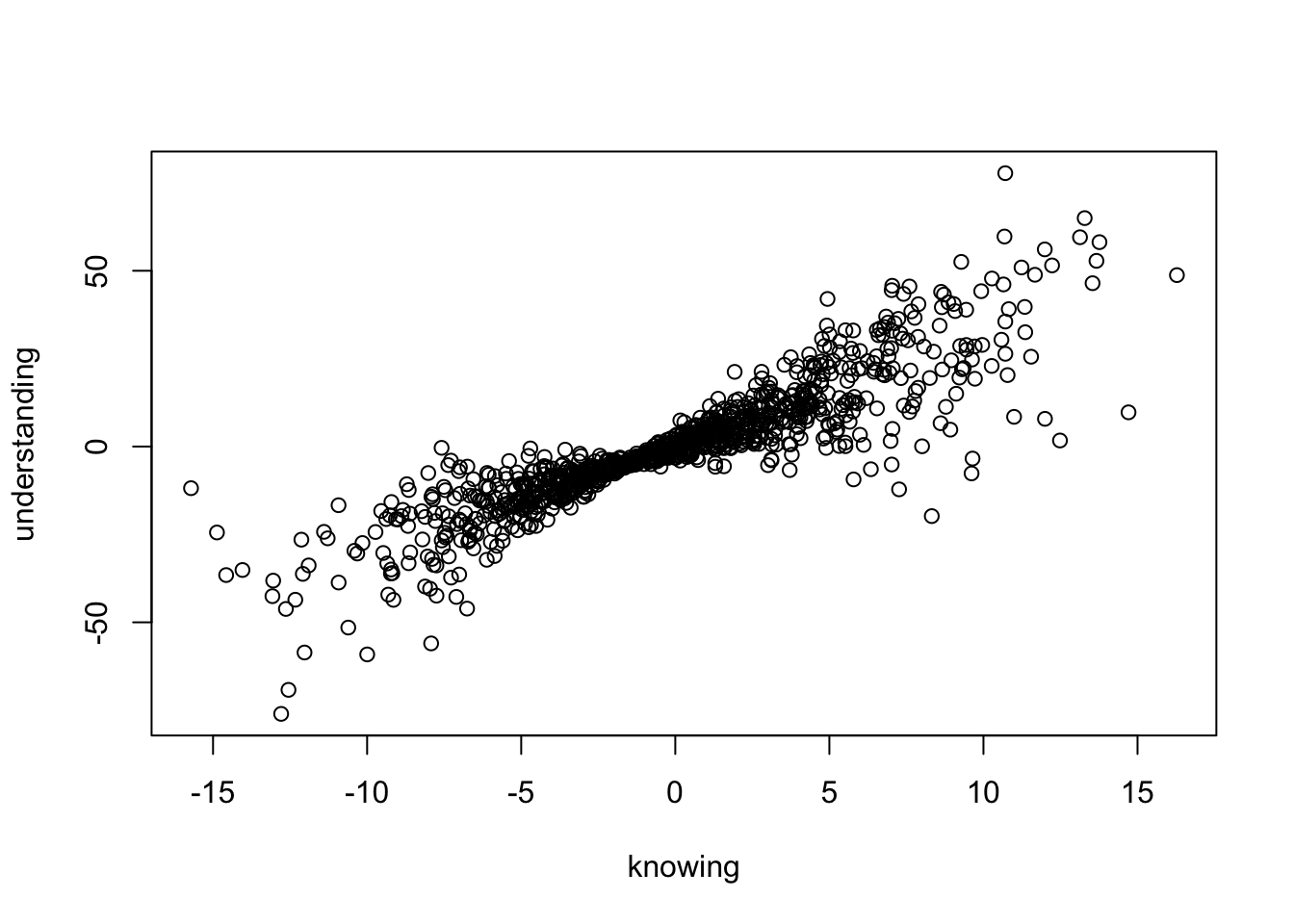
Auch dieser Plot zeigt auf, dass höhere Werte in der Variable ‘Wissen’ mit höheren Werten in der Variable ‘Verständnis’ einhergehen. Es fällt jedoch auf, dass bei sehr kleinen und sehr großen Werten von Wissen eine größere Streuung in den Werten von ‘Verständnis’ auftreten, als bei mittleren Werten von ‘Wissen’ (knowing=0).
plot (knowing, elaboration)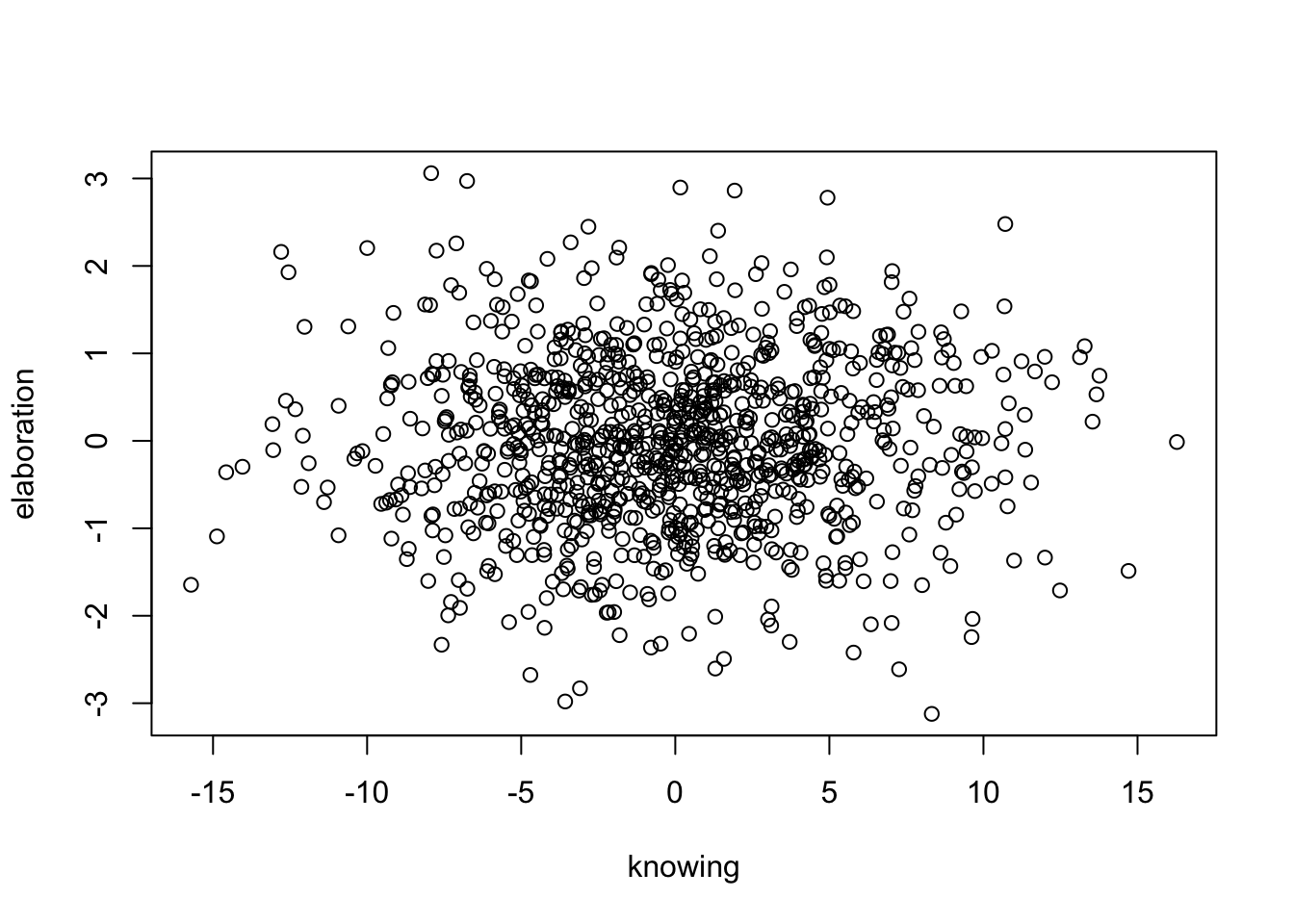
Der Zusammenhang zwischen ‘Wissen’ und ‘Vertiefung’ stellt sich unsystematisch dar. Scheinbar gibt es keinen Zusammenhang zwischen ‘Wissen’ und ‘Vertiefung’.
plot (elaboration, understanding)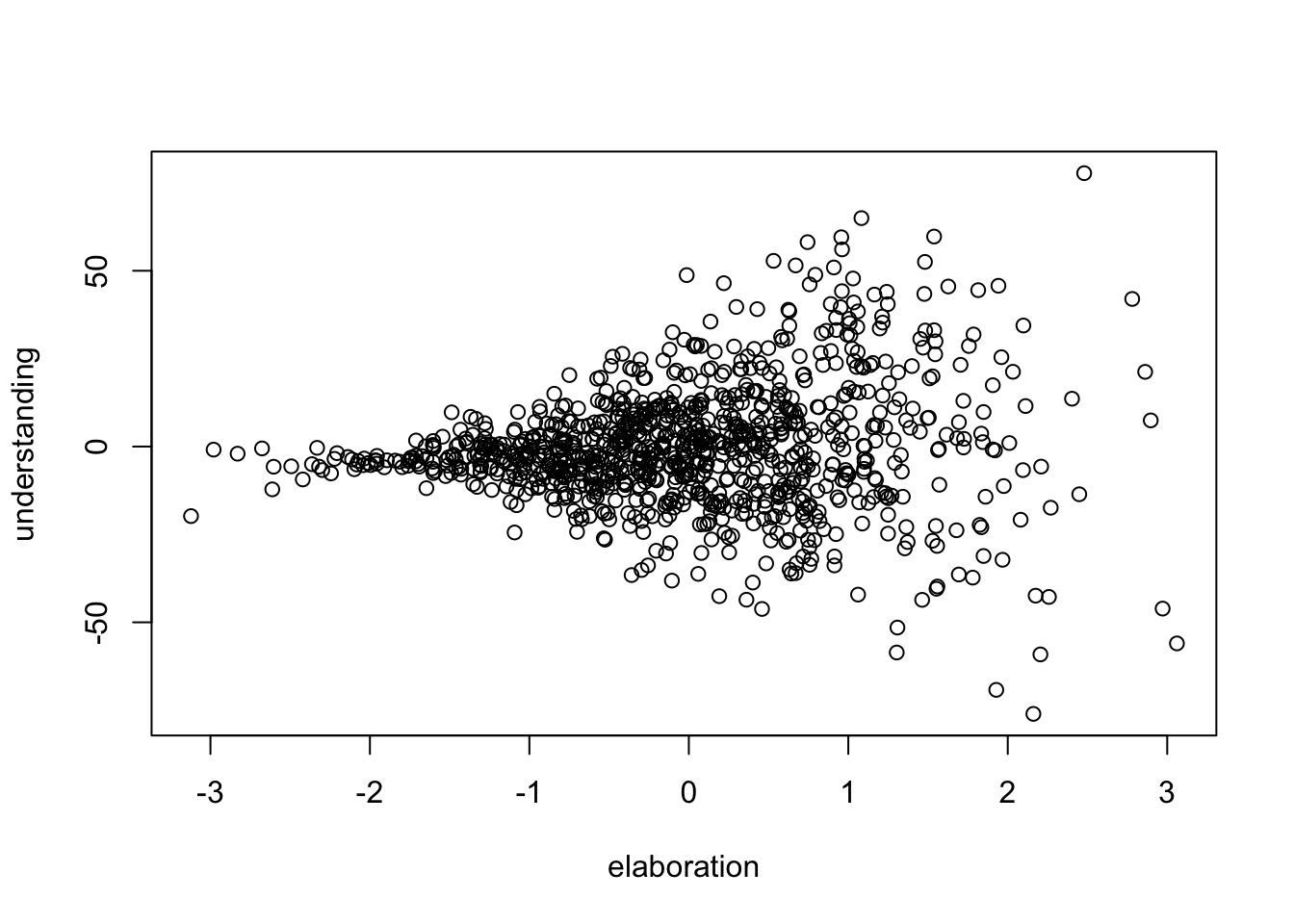
Der Zusammenhang zwischen ‘Vertiefung’ und ‘Verständnis’ zeigt auf, dass die Werte von ‘Verständnis’ mit steigender ‘Vertiefung’ eine höhere Streuung aufweisen. Allgemein formuliert, geht intensivere ‘Vertiefung’ also mit steigendem, konstantem und sinkendem Verständnis einher.
Das zu bestimmende Modell beinhaltet wieder drei Pfadkoeffizienten \(\beta\)1, \(\beta\)2 und \(\beta\)3. Anhand welcher Koeffizienten wird über diese Hypothesen entschieden?
Die erste Hypothese ( “Wissen und Elaboration interagieren in Hinsicht auf das Verständnis”) wird unterstützt, wenn der Pfadkoeffizient des Interaktionsterms (\(\beta\)3) von Wissen und Elaboration signifikant unterschiedlich von Null darstellt.
Die zweite Hypothese (“Der positive Einfluss von Wissen auf das Verständnis durch hohe Elaboration verstärkt”) erfordert es, den marginalen Effekt von Wissen auf Verständnis bei hoher Elaboration gegenüber geringer Elaboration zu vergleichen.
Wie für Regressionsmodelle mit Interaktion wird die Interaktion der interagierenden Variablen als Produktterm der mittelwertzentrierten Variablen konstruiert (Dawson, 2014).
# Interaktion/ Moderationsanalyse
# Bildung des Interaktionsterms
# (aus mittelwertzentrierten Variablenwerten)
interaction = (knowing -mean(knowing)) *
(elaboration-mean(elaboration))
moderation_data <- data.frame(cbind(knowing,
elaboration,
understanding,
interaction))
head(moderation_data)## knowing elaboration understanding interaction
## 1 10.993847506 -1.3688408 8.4511492 -15.174298731
## 2 -0.151545780 0.7031821 -0.7177007 -0.010071672
## 3 3.779447005 0.5585935 14.4147141 2.209888702
## 4 0.002531287 -0.0402375 0.4289047 -0.004842335
## 5 2.587983621 -0.9769593 1.7939653 -2.647219530
## 6 0.476003332 -0.4156754 -0.9855957 -0.251505304Wir bezeichnen das Modell mit den Namen ‘model2’ und weisen ihm Variablen und die Zusammenhänge zwischen den Variablen zu. Wieder werden die Regressionspfade in der ‘lavaan’-Syntax mit einer ‘Tilde’, Kovarianzpfade mit einer ‘Doppel-Tilde’ kodiert.
library (lavaan)
model2 <-
'understanding ~ knowing
understanding ~ elaboration
understanding ~ interaction
'model2_FIT <- sem(model2,data=moderation_data, meanstructure=TRUE)summary(model2_FIT)## lavaan 0.6-10 ended normally after 27 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 1000
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## understanding ~
## knowing 2.997 0.006 488.342 0.000
## elaboration 1.757 0.032 55.014 0.000
## interaction 1.507 0.006 248.358 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .understanding -0.024 0.031 -0.778 0.436
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .understanding 0.963 0.043 22.361 0.000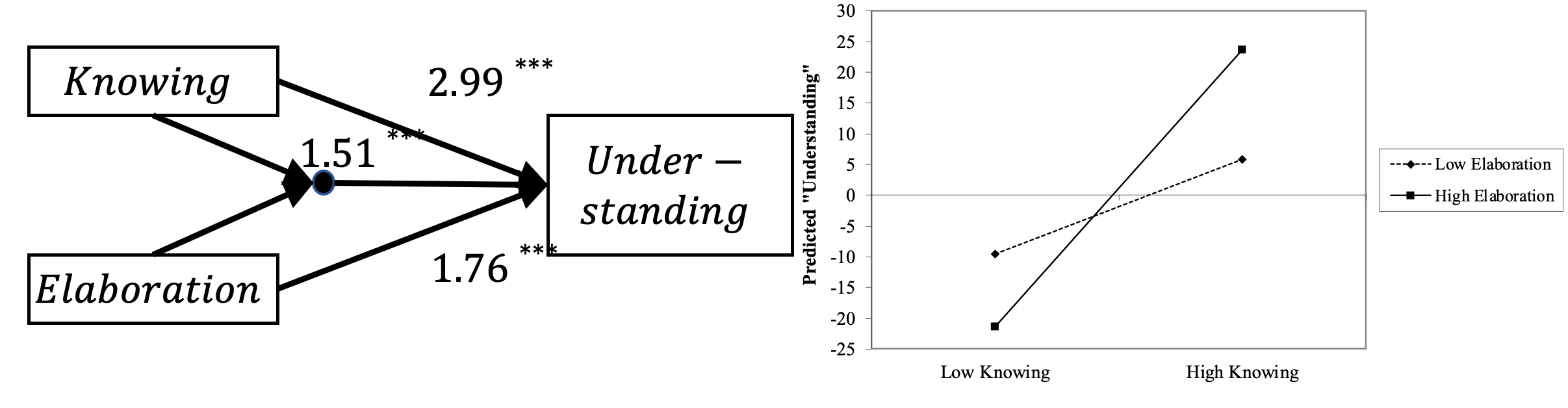
In diesem Fall ergibt sich für den Interaktionsterm ein signifikanter positiver Pfadkoeffizient (\(\beta\)3=1.51; z=248.34; p \(\leq\) 0.000).
Um die standardisierten Koeffizienten auszugeben verwenden wir die folgende Anweisung:
parameterEstimates (model2_FIT)## lhs op rhs est se z pvalue ci.lower ci.upper
## 1 understanding ~ knowing 2.997 0.006 488.342 0.000 2.985 3.009
## 2 understanding ~ elaboration 1.757 0.032 55.014 0.000 1.695 1.820
## 3 understanding ~ interaction 1.507 0.006 248.358 0.000 1.496 1.519
## 4 understanding ~~ understanding 0.963 0.043 22.361 0.000 0.878 1.047
## 5 knowing ~~ knowing 25.609 0.000 NA NA 25.609 25.609
## 6 knowing ~~ elaboration 0.128 0.000 NA NA 0.128 0.128
## 7 knowing ~~ interaction 0.830 0.000 NA NA 0.830 0.830
## 8 elaboration ~~ elaboration 0.945 0.000 NA NA 0.945 0.945
## 9 elaboration ~~ interaction -0.074 0.000 NA NA -0.074 -0.074
## 10 interaction ~~ interaction 26.166 0.000 NA NA 26.166 26.166
## 11 understanding ~1 -0.024 0.031 -0.778 0.436 -0.085 0.037
## 12 knowing ~1 -0.137 0.000 NA NA -0.137 -0.137
## 13 elaboration ~1 -0.006 0.000 NA NA -0.006 -0.006
## 14 interaction ~1 0.128 0.000 NA NA 0.128 0.128Dies unterstützt die Hypothese 1, nach welcher Wissen und Elaboration in Hinsicht auf das Verständnis interagieren.
Um die zweite Hypothese zu überprüfen bedarf es der Betrachtung des marginalen Effektes Wissen auf Verständnis. Dieser nimmt bei zunehmenden Werten des Moderators entsprechend dem positiven Koeffizienten des Interaktionsterms zu. Der marginale Effekt (‘simple slope’) von Wissen auf Verständnis kann für unterschiedliche Ausprägungen des Moderators berechnet werden nach der bekannten Gleichung (Berry et al., 2012; Brambor et al., 2006):
\[ \partial Y/\partial X_1 = \beta_1 +\beta_3X_2 \]
Das Package ‘semTools’ nimmt uns viel Aufwand ab und bestimmt die Effekte von Wissen auf Understanding für unterschiedliche Ausprägungen von Elaboration. Hier wurden die Slopes von Wissen auf Verständnis für drei Ausprägungen von Elaboration getestet. Die Ausprägung ‘geringer Elaboration’ wurde als Mittelwert minus einer Standardabweichung, mittlere Elaboration als Mittelwert und hohe Elaboration als Mittelwert plus eine Standardabweichung definiert.
library (semTools)
result2WayMC <- probe2WayMC (model2_FIT,
nameX=c("knowing",
"elaboration",
"interaction"),
nameY="understanding",
modVar="elaboration",
valProbe=c(-1,0,1))
result2WayMC## $SimpleIntcept
## elaboration est se z pvalue
## 1 -1 -1.781 0.044 -40.083 0.000
## 2 0 -0.024 0.031 -0.778 0.436
## 3 1 1.733 0.045 38.814 0.000
##
## $SimpleSlope
## elaboration est se z pvalue
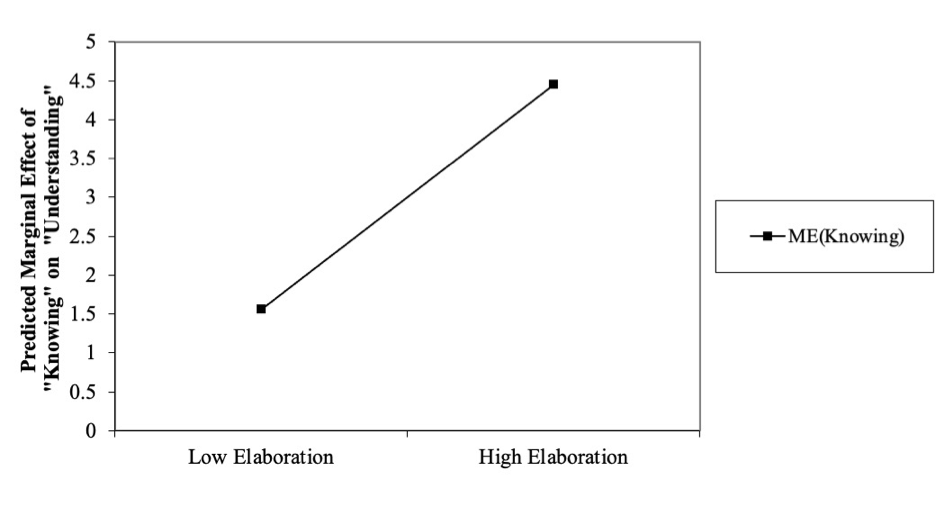
## 1 -1 1.489 0.009 169.818 0
## 2 0 2.997 0.006 488.342 0
## 3 1 4.504 0.008 530.535 0plotProbe (result2WayMC,
xlim=c(-1,1), # Bereich der x-Achse
xlab = "knowing",
ylab = "predicted understanding")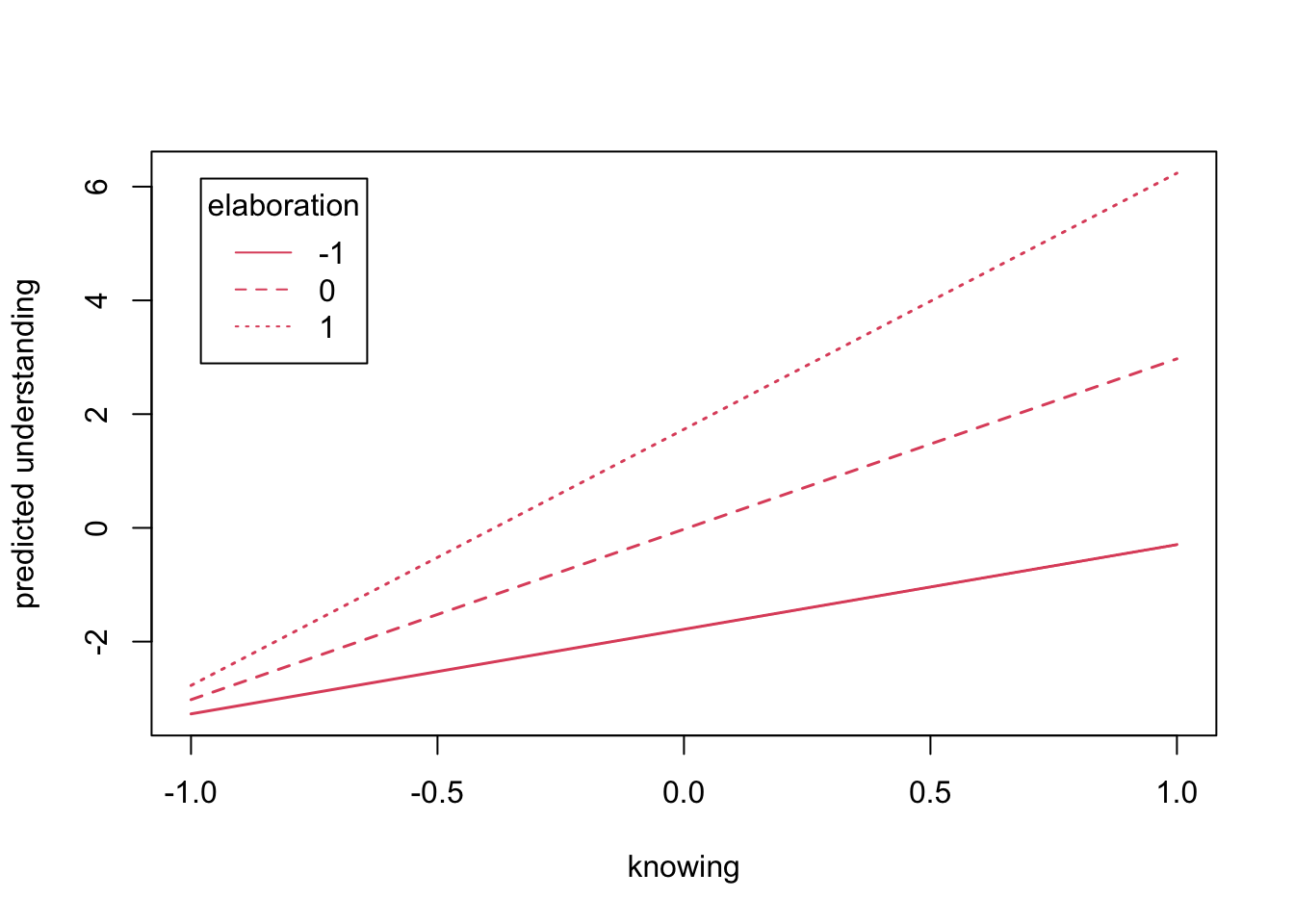
Das Ergebnis zeigt uns auf, dass für Wissen bei geringer Elaboration einen marginalen Effekt von ME=1.49 (z=169.82, p=0.000) vorliegt. Bei hoher Elaboration fällt dieser Effekt höher aus (ME=4.50; z=530.54, p=0.000). Dies unterstützt die zweite Hypothese, nach welcher der positive Effekt von Wissen auf Verständnis durch Elaboration verstärkt wird. Aber ist der Anstieg des marginalen Effektes von 1.49 auf 4.5 auch signifikant?
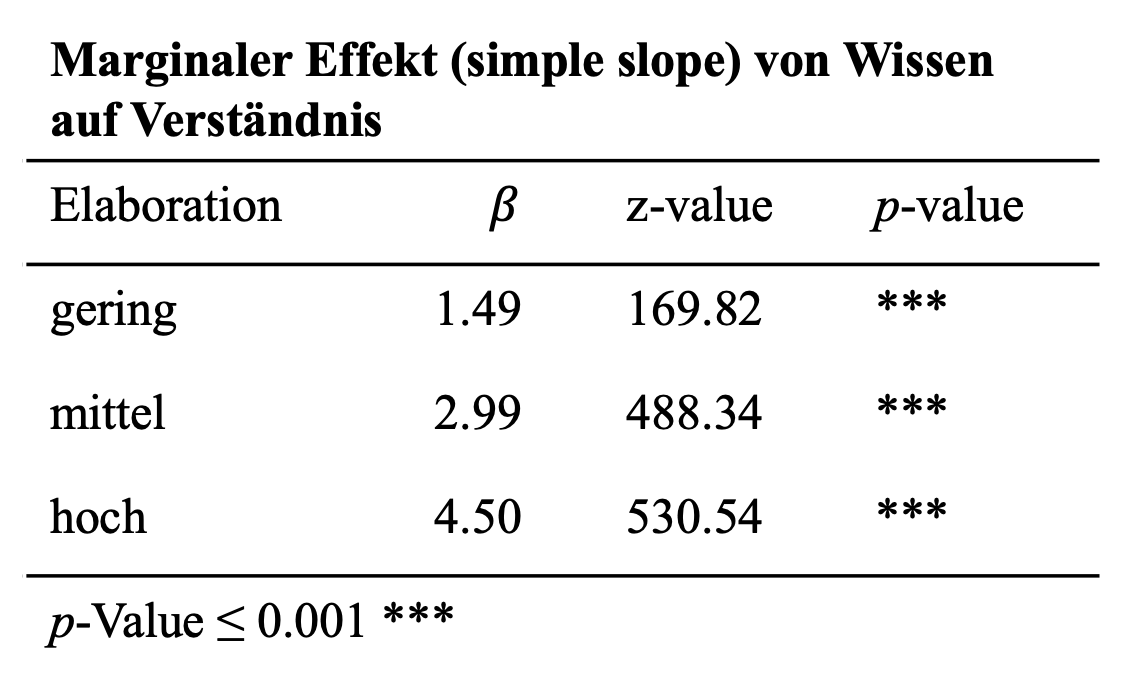
Um die Differenz auf Signifikanz zu testen, kann eine alternative Möglichkeit genutzt werden.
Vor dem Hintergrund, dass sich die Anstiege aus der oben dargestellten Gleichung bestimmen lassen, kann die folgende Anpassung weiterhelfen. Wir benötigen die Koeffizienten \(\beta\)1 und \(\beta\)3. Diese können wir, wie bereits weiter oben beschrieben, aus dem Modell extrahieren und mit dem Wissen um Mittelwert und Standardabweichung von Elaboration einzelne Terme für die unterschiedlichen Ausprägungen von Elaboration sowie deren Differenz definieren.
# Alternative Bestimmung mit Hilfe von Labels
model2 <-
'understanding ~ beta1*knowing
understanding ~ elaboration
understanding ~ beta3*interaction
# die Standardabweichung von Elaboration ist SD=0.97
slope_at_moderator_low := beta1 + (beta3 * (-0.97))
slope_at_moderator_high := beta1 + (beta3 * (+0.97))
slope_diff := slope_at_moderator_high -
slope_at_moderator_low
'
model2_FIT <- sem(model2,data=moderation_data,
meanstructure=TRUE)
summary(model2_FIT)## lavaan 0.6-10 ended normally after 27 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 5
##
## Number of observations 1000
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## understanding ~
## knowing (bet1) 2.997 0.006 488.342 0.000
## elabrtn 1.757 0.032 55.014 0.000
## intrctn (bet3) 1.507 0.006 248.358 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .understanding -0.024 0.031 -0.778 0.436
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .understanding 0.963 0.043 22.361 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## slp_t_mdrtr_lw 1.535 0.009 177.591 0.000
## slp_t_mdrtr_hg 4.459 0.008 533.049 0.000
## slope_diff 2.924 0.012 248.358 0.000parameterEstimates (model2_FIT)## lhs op rhs
## 1 understanding ~ knowing
## 2 understanding ~ elaboration
## 3 understanding ~ interaction
## 4 understanding ~~ understanding
## 5 knowing ~~ knowing
## 6 knowing ~~ elaboration
## 7 knowing ~~ interaction
## 8 elaboration ~~ elaboration
## 9 elaboration ~~ interaction
## 10 interaction ~~ interaction
## 11 understanding ~1
## 12 knowing ~1
## 13 elaboration ~1
## 14 interaction ~1
## 15 slope_at_moderator_low := beta1+(beta3*(-0.97))
## 16 slope_at_moderator_high := beta1+(beta3*(+0.97))
## 17 slope_diff := slope_at_moderator_high-slope_at_moderator_low
## label est se z pvalue ci.lower ci.upper
## 1 beta1 2.997 0.006 488.342 0.000 2.985 3.009
## 2 1.757 0.032 55.014 0.000 1.695 1.820
## 3 beta3 1.507 0.006 248.358 0.000 1.496 1.519
## 4 0.963 0.043 22.361 0.000 0.878 1.047
## 5 25.609 0.000 NA NA 25.609 25.609
## 6 0.128 0.000 NA NA 0.128 0.128
## 7 0.830 0.000 NA NA 0.830 0.830
## 8 0.945 0.000 NA NA 0.945 0.945
## 9 -0.074 0.000 NA NA -0.074 -0.074
## 10 26.166 0.000 NA NA 26.166 26.166
## 11 -0.024 0.031 -0.778 0.436 -0.085 0.037
## 12 -0.137 0.000 NA NA -0.137 -0.137
## 13 -0.006 0.000 NA NA -0.006 -0.006
## 14 0.128 0.000 NA NA 0.128 0.128
## 15 slope_at_moderator_low 1.535 0.009 177.591 0.000 1.518 1.551
## 16 slope_at_moderator_high 4.459 0.008 533.049 0.000 4.443 4.475
## 17 slope_diff 2.924 0.012 248.358 0.000 2.901 2.947Die resultierende Koeffizienten-Differenz in Höhe von 2.92 (z=248.358; p=0.000) ist signifikant und lässt endgültig die Bestätigung der Hypothese zu, dass hohe Elaboration den positiven Zusammenhang zwischen Wissen und Verständnis signifikant erhöht.
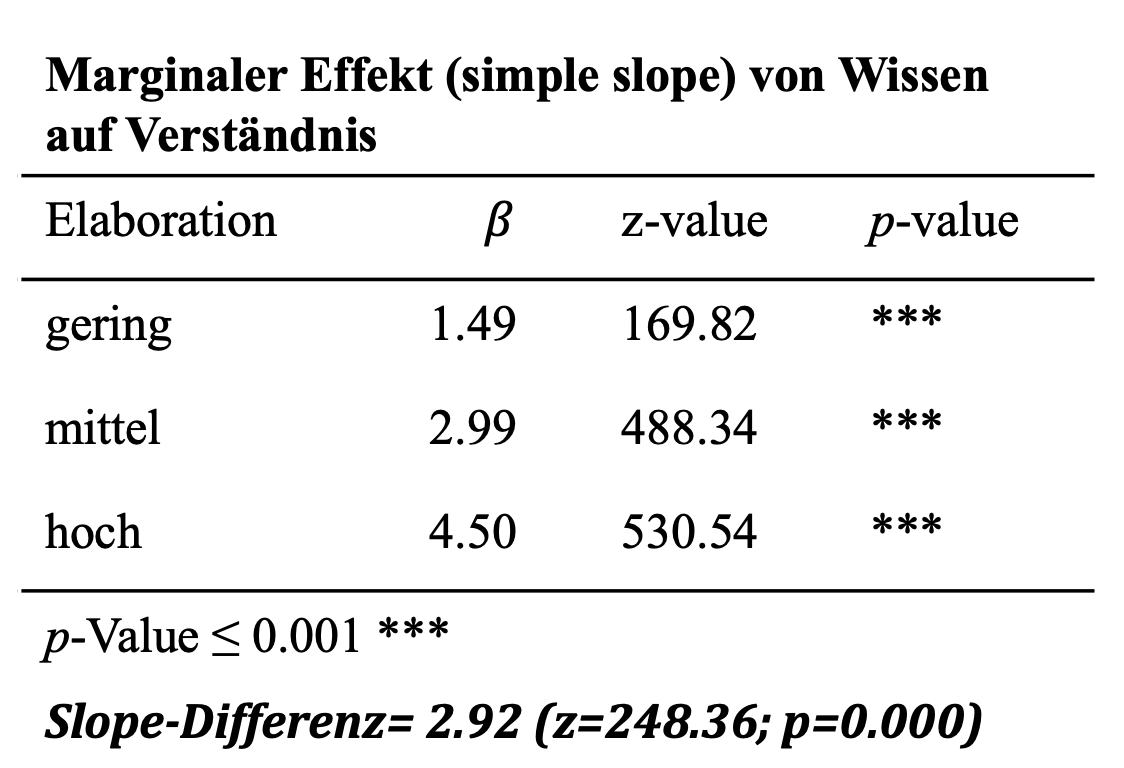
Literatur
Bei korrelierenden unabhängigen Variablen kann das sogenannte Problem der Multikollinearität auftreten. Vereinzelt wurde das Problem auf hoch ausfallende Standardfehler fokussiert, was dann mit einem geringeren Testwert und entsprechend schlechteren p-Wert dargestellt wird. Eine andere Sichtweise bezieht sich auf die “ceteris paribus” Bedingung, welche die Annahme bezeichnet, dass alle anderen relevanten Faktoren konstant bleiben (Westermann, 2000, S. 156). Bei hoher Korrelation der Prädiktoren im multivariaten Regressionmodell ist diese Bedingung mglw. nicht erfüllt und die Koeffizienten sind dementsprechend zu interpretieren. Die Perspektive der konditionalen Unabhängigkeit kann hierbei hilfreich sein.↩︎