Kapitel 1 Einleitung
“Jedes Handwerkszeug enthält in seiner Form und seiner Materialität bereits eine ‘Theorie’ seines Gegenstandes: Der Hammer ist so wie er ist, weil er sich aus der Praxis des Nageleinschlagens ergeben hat und das gilt vergleichbar auch für den Meißel, die Säge, den Füller, den Anspitzer und alle Dinge, die geeignet sind, bestimmte Aufgaben effektiv zu erledigen. Wer mit einer Spitzhacke einem Zahn im Mund zu Leibe rückt wird ebenso scheitern wie der, welcher das Fieberthermometer nutzt, um Erbsen zu zählen. Das ist trivial – ohne Zweifel. Nicht trivial ist dagegen der Befund, dass diese Trivialität oft vergessen wird”. (Baur & Blasius, 2014, S. 68)
Allgemeinen Aussagen zur Folge sind die Wirtschaftswissenschaften in ein übergeordnetes Wissenschaftssystem eingebettet, in dem Wissen und Entscheidungen als Resultat spezifischer Annahmen, Konzepte und Methoden zugänglich, nachvollziehbar und anschlussfähig werden (Herrmann, 1996).
Auch Strukturgleichungsmodelle, auf die ich in diesem Kurs zu sprechen komme, finden dabei ein zunehmendes Interesse. Um die Anschlussfähigkeit zum Projektseminar herzustellen, werde ich am Anfang etwas weiter ausholen und auf den Bezug zwischen Empirischer Forschung und den Wirtschaftswissenschaften eingehen.
Weiter gefasst und den Sozialwissenschaften zugeordnet, verfolgen die Wirtschaftswissenschaften die Zielsetzung, menschliches Verhalten wissenschaftlich zu beschreiben, zu erklären, zu prognostizieren und rational zu gestalten (Colbe & Laßmann, 1974, S. 2).
Dabei geht also einerseits darum Phänomene und Zusammenhänge aufzuzeigen und zu erklären, um möglichst gesicherte Erkenntnisse zu finden und andererseits darum, zukünftige Vorgänge zu prognostizieren und optimale Handlungsweisen für gegebene Ziele zu bestimmen (Entscheidungslogik) (Döring & Bortz, 2016, S. 5). Diese Problemstellungen der Sozialwissenschaften betreffen damit mehr oder weniger konkrete Aspekte der direkten Erfahrungswelt, womit die Sozialwissenschaften im Bereich der Realwissenschaften (also der Erfahrungs- und empirischen Wissenschaften) verortet sind.
Die empirische Forschung im Rahmen der Wirtschaftswissenschaften gibt also eine wissenschaftliche Methodik vor, um die als zielgerichtet angesehenen Handlungen und Entscheidungen von Individuen und Gruppen als betriebliches Geschehen im gewerblichen Bereich der Wirtschaft zu beschreiben, sowie die damit verbundenen Prozesse und Strukturen aufzuzeigen, nachzuweisen und mögliche Prognosen über zukünftige Ereignisse zu treffen.
Die Formulierung der interessierenden Fragestellungen weisen dabei eine hohe Bedeutung auf, weil die systematische Überprüfung von Theorien nicht nur voraussetzt, dass theoretische Überlegungen vorliegen, sondern auch, dass sich aus theoretischen Modellen empirische Konsequenzen ableiten lassen (Schnell, Hill & Esser, 2008, S. 7). Dabei beinhaltet die Art und Weise der Fragestellung häufig auch die Bedingungen für Messung und Methoden.
Im ersten Semester des Projektseminares waren wir auf die Erhebung von Daten (z.B. mittels Befragung) eingegangen und haben verschiedene Methoden (Kovarianz und Regression) behandelt, die dafür geeignet erscheinen, bi-variate und multivariate Zusammenhänge aufzuzeigen bzw. nachzuweisen. Diese Techniken eignen sich dafür, die Strukturen zwischen gemessenen Variablen durch mathematische Gleichungen aufzudecken und einfache Zusammenhänge zu überprüfen.
Dabei wurde darauf verwiesen, dass Korrelation nicht mit Kausalität gleichzusetzen ist. So geht ‘das Krähen des Hahnes mit dem Sonnenaufgang einher, verursacht es aber nicht’ (Pearl & Mackenzie, 2018, S. 5) und die bestehende Korrelation zwischen dem ‘Nisten von Störchen und höheren Geburtenraten’ zeigt nicht auf, ‘dass der Storch die Babys bringt’.
Weiterhin wurde darauf hingewiesen, dass der Zahlenwert des Zusammenhangsmaße unter bestimmten Umständen ein falsches Ergebnis liefern kann. Dieses Phänomen haben wir unter der Bezeichnung ‘Endogenität’ kennen gelernt und als Ursache die konditionale Unabhängigkeit bzw. konditionale Abhängigkeit von Variablen dargestellt.
Als kurze Wiederholung sei hier angemerkt, dass die konditionale Unabhängigkeit zwischen zwei Variablen dann besteht, wenn die Unabhängigkeit zwischen zwei Variablen durch die Auswirkung bzw. dem Einwirken einer dritten Variablen besteht. D.h. das berechnete Zusammenhangsmaß zweier Variablen ist durch den Einfluss einen dritten Variablen gleich Null oder weicht nicht signifikant von Null ab.
Solche dritte Variablen bezeichnet man als Störvariablen (confounder). Insbesondere dann, wenn Methoden der empirischen Forschung nicht der Überprüfung von theoretischen Annahmen, sondern dem Aufdecken von Zusammenhängen zur Theoriebildung angewandt werden, können also radikale Fehlschlüsse auftreten. Sie betreffen zum einen die Richtung des Zusammenhanges zwischen Variablen und zum anderen die Stärke des Zusammenhanges.
An ein paar Beispielen sei dies noch einmal verdeutlicht.
1.1 Beispiel 1: Google

Die New York Times berichtete im März 2019 über eine Studie zum geschlechterspezifischen Lohngefälle bei Google.1
Zur Überraschung der meisten und entgegen der Behauptungen des Arbeitsministeriums wurde festgestellt, dass Männer in ähnlichen Positionen weniger Geld erhielten als Frauen. In der Konsequenz wurde dieses Ergebnis als Diskriminierung männlicher Mitarbeiter gewertet und ihre Bezahlung erhöht. Wie kann es zu einem solchen Ergebnis kommen und beinhaltet es möglicherweise eine konstruierte Verzerrung?
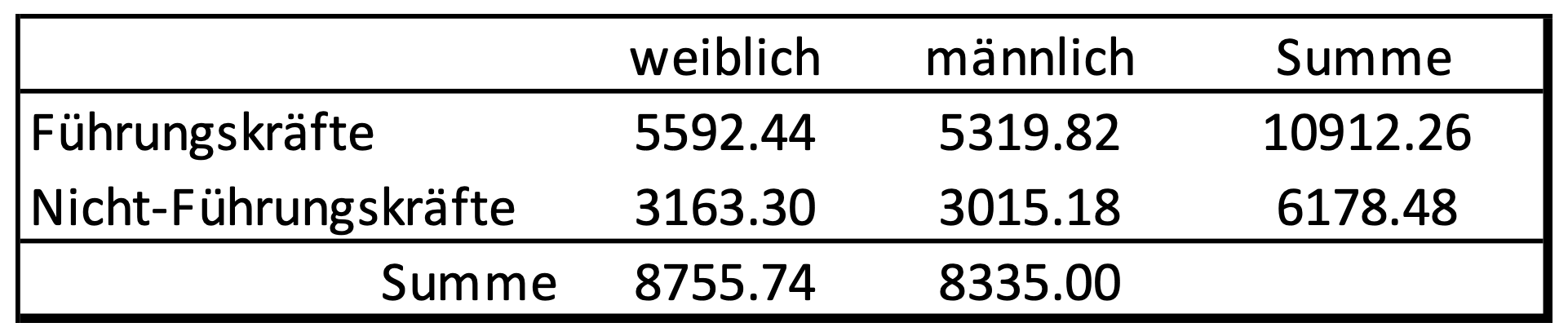
Tabelle: Mittlerer Lohn für weibliche und männliche Angestellte in Führungs- sowie Nicht-Führungspositionen
In diesem Beispiel wird Geschlechtergerechtigkeit im Sinne von Einkommensgleichheit bei gleicher Tätigkeit angesehen. Tabelle 1 bildet das mittlere Einkommen von weiblichen und männlichen Angestellten unter den Führungskräften und Nicht-Führungskräften ab. Wie zuvor berichtet, zeigt sich ein höherer Lohn sowohl bei weiblichen Führungskräften gegenüber männlichen Führungskräften als auch bei weiblichen Nicht-Führungskräften gegenüber männlichen Nicht-Führungskräften. Ist damit die Frage nach der Geschlechtergerechtigkeit ausreichend geklärt!?

Tabelle: Beobachtete und erwartete Häufigkeiten für weibliche und männliche Angestellte in Führungspositionen
Angenommen in diesem Unternehmen sind 41 männliche und 13 weibliche Führungskräfte angestellt. Kann man davon ausgehen, dass dieser Unterschied zufällig zustande gekommen ist? Die Antwort auf diese Frage ist davon abhängig, wie wir die Nullhypothese formulieren. Man kann einmal überprüfen, ob dieses Zahlenverhältnis mit der H0 vereinbar ist, dass die Anzahl männlicher und weiblicher [Führungskräfte] mit dem allgemeinen Geschlechterverhältnis 50:50 übereinstimmt. Für diesen Fall wäre zu erwarten, dass ebenso viele weibliche wie männliche Mitarbeiter in Führungspositionen angestellt sind. Mit einem \(chi^2\)(df)=14.5(1) und dem korrespondierendem p-Wert ≤0.001 würde das Ergebnis die Nullhypothese (‘Die Anzahl männlicher und weiblicher Führungskräfte stimmt einem Geschlechterverhältnis von 50:50 überein’) zurückweisen.

Tabelle: Häufigkeit für weibliche und männliche Angestellte in Führungs-sowie Nicht-Führungspositionen
Eine zweite H0 könnte behaupten, dass das Verhältnis männlich zu weiblich bei den Führungskräften dem Verhältnis männlich zu weiblich bei den Nicht-Führungskräften entspricht. Auch diese Annahme würde zurückgewiesen werden. Eine dritte H0 könnte behaupten, dass das Verhältnis männlich zu weiblich bei den Führungskräften dem Verhältnis männlich zu weiblich im gesamten Unternehmen entspricht (Bortz, 1993, S. 147). Die Referenz entscheidet in diesem Fall letztlich darüber, wie das Ergebnis zu interpretieren ist.
Allen Ergebnissen gemeinsam wird hier aufgezeigt, dass die Geschlechtergerechtigkeit eben nicht allein über das konkrete Einkommen in einer Position aufgezeigt werden kann, sondern auch die Wahrscheinlichkeit in einer solchen Positionen zu arbeiten einschließt.
Wie bereits aufgezeigt, ist die Wahrscheinlichkeit für weibliche Angestellte in Führungspositionen signifikant geringer als für männliche Angestellte. Um eine generelle Aussage zum durchschnittlichen Einkommen von weiblichen und männlichen Angestellten zu treffen, wäre demnach eine Gewichtung notwendig.

Tabelle: Berechnung der gewichteten arithmetischen Mittel
Das gewichtete arithmetische Mittel für weibliche Angestellte ergibt sich als Summe der Produkte von Häufigkeit und Einkommen, geteilt durch die gesamte Anzahl der weiblichen Angestellten.
Demnach erzieht eine weibliche Angestellte ein durchschnittliches Einkommen von 3479.09 und damit 480.99 weniger als ein männlicher Angestellter mit einem durchschnittlichen Einkommen von 3960.08. Dieses Ergebnis zeigt auf, dass ein geringeres Einkommen doch vom Geschlecht abhängig ist. Vereinfacht ausgedrückt spiegelt diese Operationalisierung ‘Geschlechtergerechtigkeit’ im Sinne von Verteilungsgerechtigkeit wider.
1.2 Beispiel 2: Education and Salary (Simulation data)
Derartige Fehlschlüsse treten in gleicher Weise auch in anderen Techniken, wie zum Beispiel Regressionen, auf. In einem Datensatz von 1000 Mitarbeitern eines Unternehmens werden die drei Faktoren Bildung (education), hierarchisches Level (management) und Gehalt (salary) berücksichtigt.
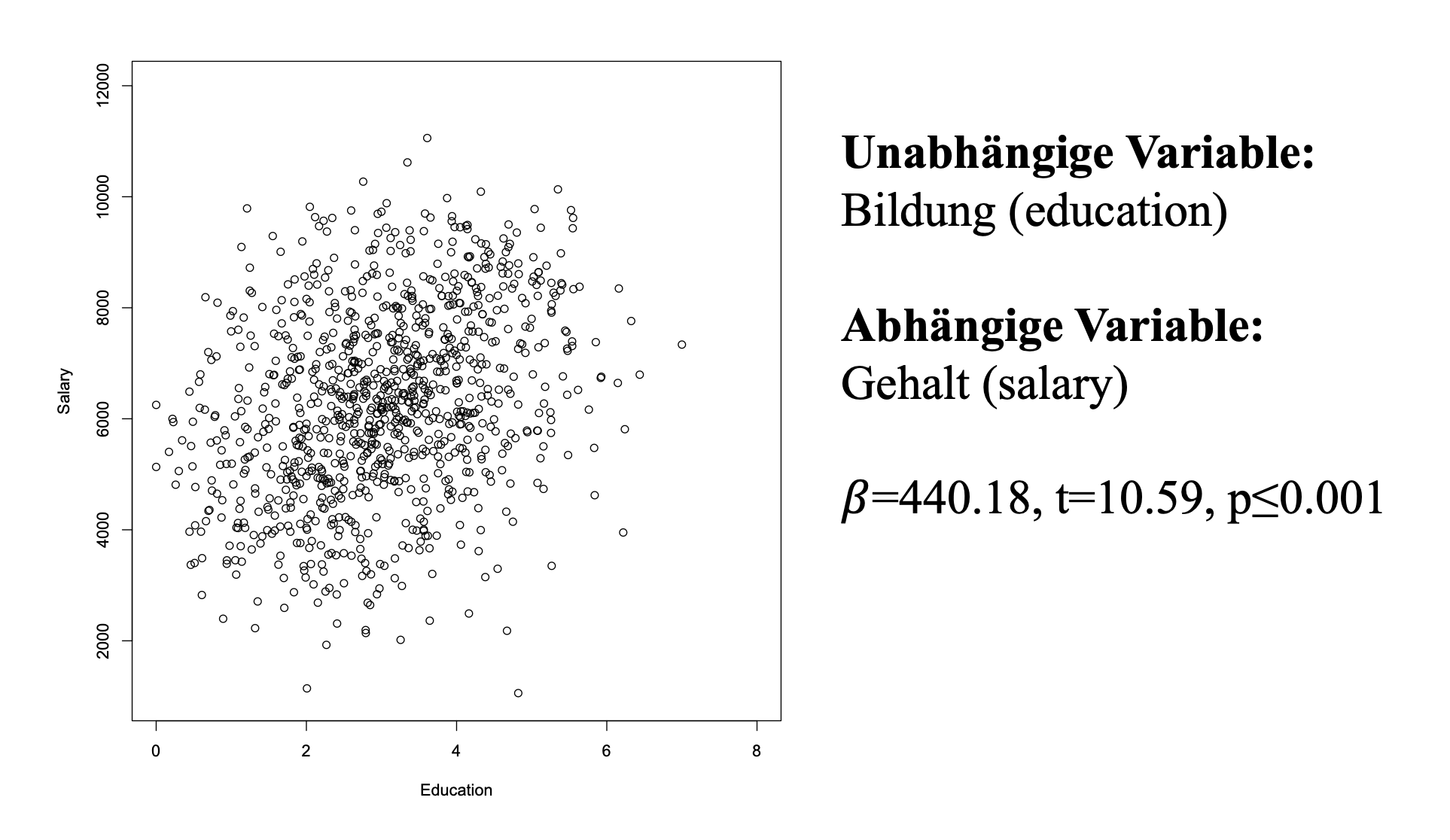
Der Plot des Zusammenhangs von Bildung und Gehalt lässt einen positiven Trend vermuten, der sich in einer Regressionsanalyse bestätigt. Mit einem signifikant positiven Regressionskoeffizienten (\(\beta\)=440.18, t=10.59, p≤0.001) wird ein positiver Zusammenhang zwischen Bildung und Gehalt aufgezeigt.
Betrachten wir die gleiche Fragestellung unter Berücksichtigung hierarchischer Level, also auf unterschiedlichen Ebenen des Managements, weist die Analyse ein gegenteiliges Ergebnis hin. Auf allen drei hierarchischen Stufen wird ein negativer Zusammenhang zwischen Bildung und Gehalt erkennbar. Über derartige Aspekte der Datenstruktur sollten wir uns im Folgenden immer bewusst sein.
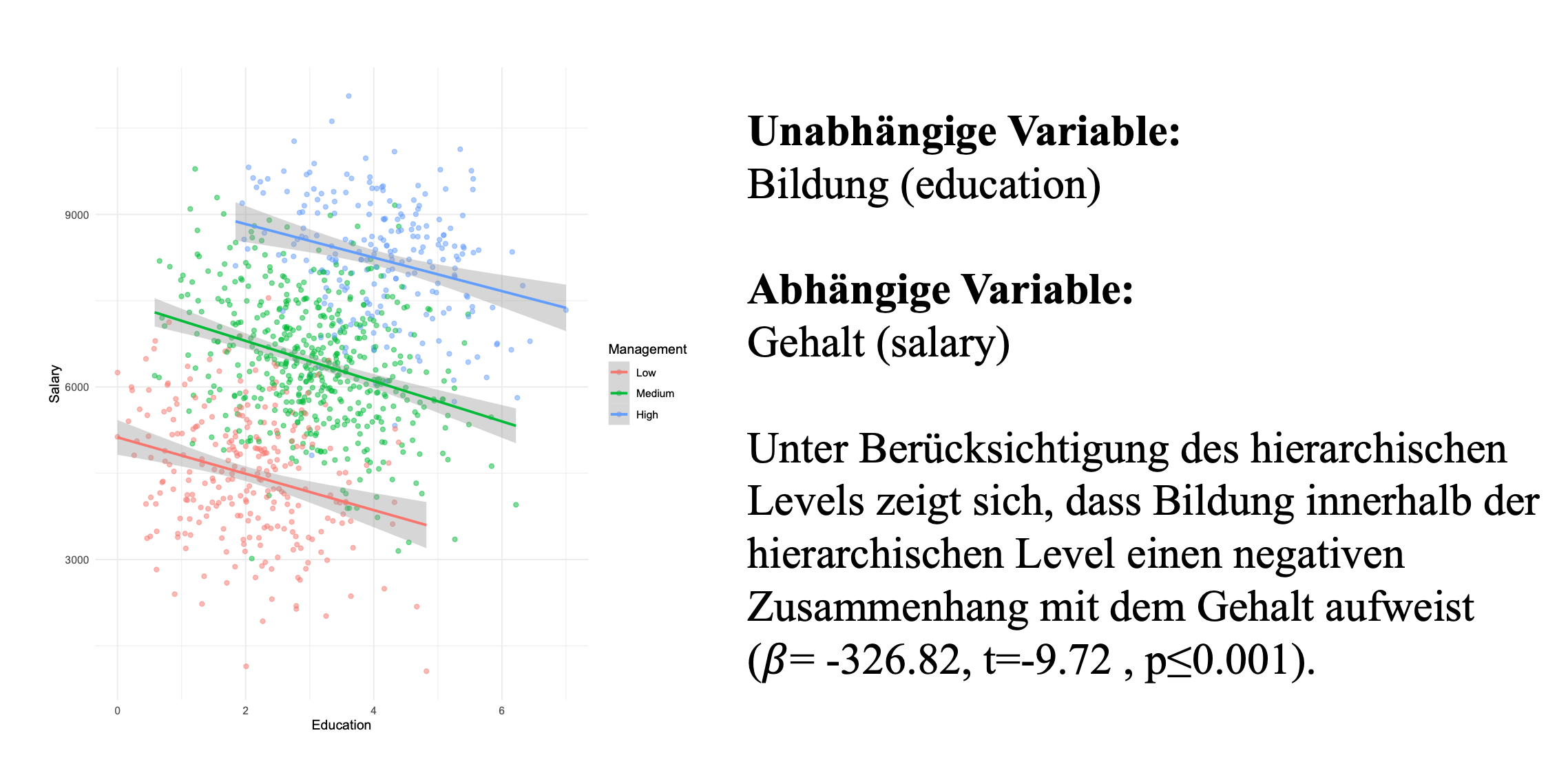
Unerwartete Ergebnisse sind insofern keine schlechteren Ergebnisse, sondern sie sollen dazu anregen, die Gründe für Diskrepanz von Erwartung und Ergebnissen zu erklären.
Häufig wird der Forschende an dieser Stelle gezwungen, weitere Aspekte in seine Überlegungen einfließen zu lassen, weil selbst einfache Zusammenhänge zwischen zwei Variablen durch weitere Faktoren bestimmt sein können.
Mit zunehmender Anzahl von Variablen werden jedoch andere Probleme auftreten, die für andere Methoden (als die einfache Regressionsanalyse) sprechen. Dies wird in folgendem Beispiel deutlich.
1.3 Beispiel 3: Corporate venture planning
Sie sehen die Ergebnisse von vier Regressionsmodellen.2 Im ersten Modell wurden Kontrollvariablen verwendet, um die abhängige Variable ‘corporate venture planning’ zu prognostizieren. ‘Corporate venture planning’ steht in diesem Artikel für ‘Planungsautonomie’.
In dieser unvorteilhaften Darstellungsform sind die p-Werte der Regressionskoeffizienten in eckigen Klammern aufgeführt. Eine der Kontrollvariablen, die ‘Anzahl der Mitarbeiter im Mutterunternehmen’ weist mit einem p-Wert von 0.06 auf einen tendenziell signifikanten Koeffizienten hin. Im zweiten Regressionsmodell wurden zwei weitere Variablen in das Modell eingefügt: Mark-Vertrautheit und Produkt-Ähnlichkeit. Beide Variablen weisen keine signifikanten Regressionskoeffizienten auf. Trotzdem verändert sich der p-Wert des Regressionskoeffizienten für ‘Anzahl der Mitarbeiter im Mutterunternehmen’ in diesem Modell auf einen Wert von 0.46. Worauf würde dies hindeuten?
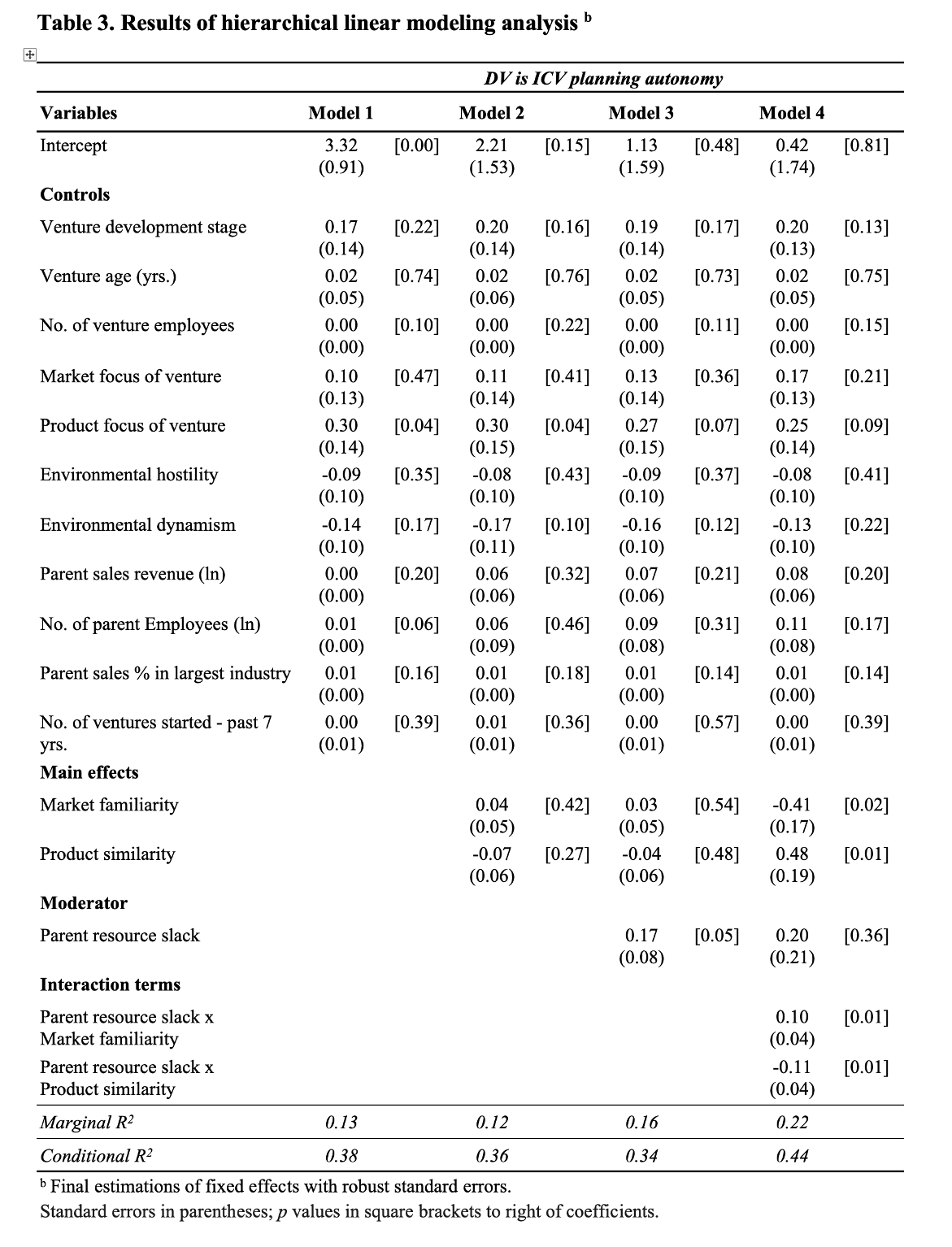
Es ist wahrscheinlich, dass sich die geschätzten Parameter der Kontrollvariablen durch die Hinzunahme weiterer Variablen verändert haben.
Vor dem Hintergrund der konditionalen Unabhängigkeit wäre zu argumentieren, dass der Zusammenhang zwischen der Variablen ‘Anzahl der Mitarbeiter’ und ‘Planungsautonomie’ in diesem Modell konditional unabhängig ist. Das bedeutet, die Unabhängigkeit in Modell 2 ist durch den Einfluss einer dritten Variable verursacht. Die entscheidende ‘Drittvariable’ könnte in diesem speziellen Fall eine der hinzugefügten Variablen ‘Mark-Vertrautheit’ oder ‘Produkt-Ähnlichkeit’ sein.
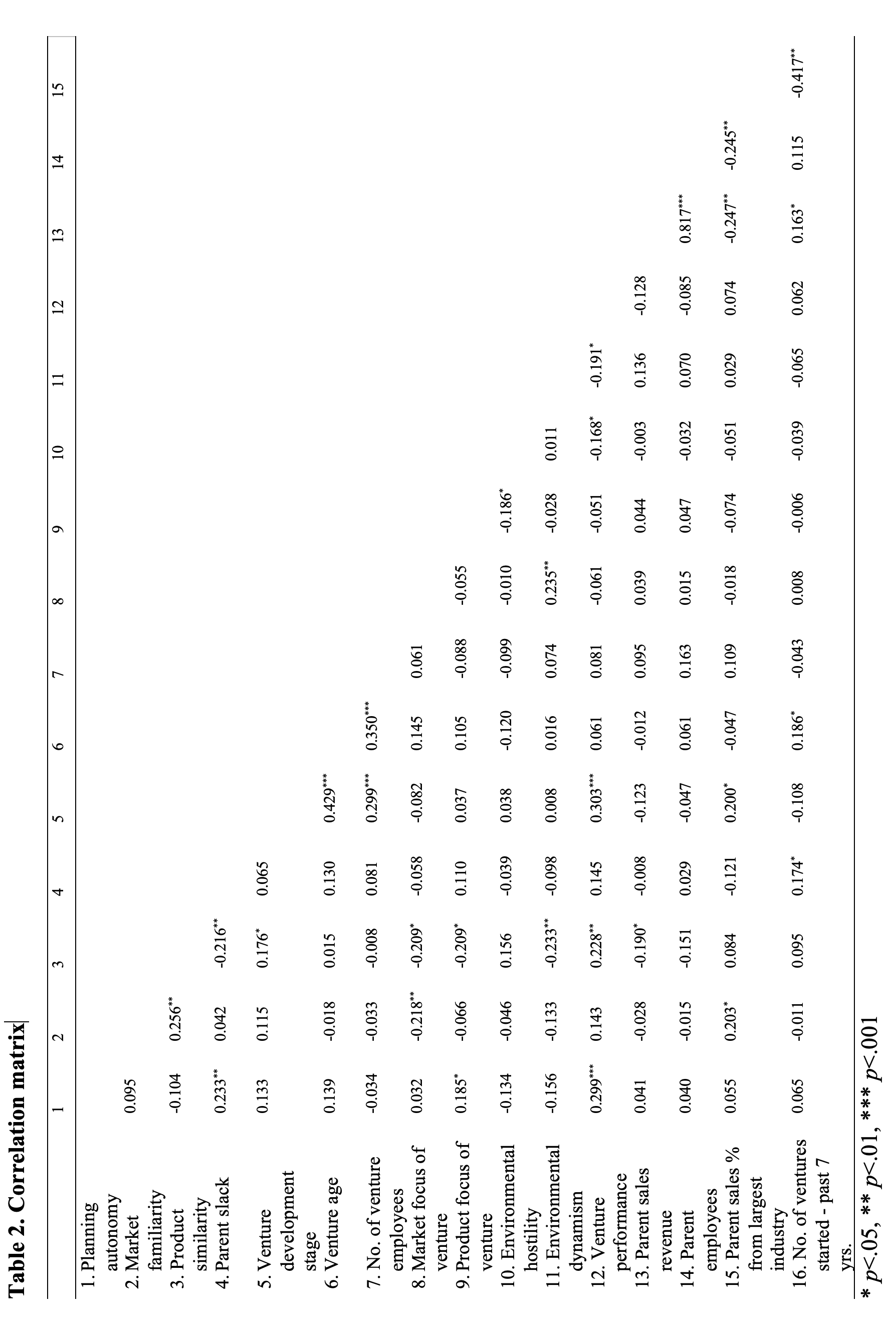
Da keine der beiden Variablen einen signifikanten Koeffizienten hinsichtlich der abhängigen Variablen ‘Planungsautonomie’ aufweist, ist die Form einer Kette (‘chain’) unwahrscheinlich. Die Formen der Gabel (‘fork’) und der Kollision (‘collider’) sind aus der Korrelationstabelle nicht ersichtlich.
Literatur
When Google conducted a study recently to determine whether the company was underpaying women and members of minority groups, it found, to the surprise of just about everyone, that men were paid less money than women for doing similar work (https://www.nytimes.com/2019/03/04/technology/google-gender-pay-gap.html)↩︎
Werden zusätzliche Variablen zur Kontrolle in ein Regressionsmodell einbezogen, wird traditionell eine hierarchische Regression angewandt. Dabei wird ein Regressionsmodell bestimmt, in dem die Kontrollvariablen als Prädiktoren für die abhängige Variable fungieren. Im nächsten Schritt werden dann die interessierenden unabhängigen Variablen in das Modell eingefügt. Nur wenn dadurch ein signifikanter Anstieg im Determinationskoeffizienten R2 erreicht wird, gilt die unabhängige Variable als sinnvoller Prädiktor für die abhängige Variable. Dies ist ein Grund, warum viele Journale die R2 für die einzelnen Modelle verlangen.↩︎