Kapitel 4 SEM und Hypothesentestung
Im letzten Kapitel wurde besprochen, wie die Zuordnung von manifesten Variablen zu latenten Konstrukten mit einer konfirmatorischen Faktorenanalyse überprüft werden kann. Dabei wurden zwei Aspekte deutlich. Zum einen galt es, die Messung der theoretischen Konstrukte in Hinsicht auf Reliabilität und Validität zu beurteilen und zum anderen ging es darum, die Güte des Modells insgesamt zu bewerten.
Am Ende des Beitrages hatte ich kurz erwähnt, dass als Ergebnis der konfirmatorischen Faktorenanalyse die Werte der latenten Variablen mit der Anweisung ‘lavPredict’ gespeichert werden können, um sie beispielsweise für Plots oder Regressionsanalysen verfügbar zu machen.
Hier werde ich anknüpfen, bevor ich dann auf die Hypothesentestung durch das Strukturgleichungsmodell zu sprechen komme.
# Speichern der Werte der latenten Variablen
fscores <- as.data.frame(lavPredict(CFA_FIT))
head(fscores)## Vertrauen Vertrag BMI
## 1 -0.19251645 -1.55190281 -0.6349184
## 2 -0.15433512 0.18029853 0.3080957
## 3 0.20909812 0.19819078 0.3044153
## 4 -0.89389719 0.15416892 1.0002662
## 5 0.06892823 -0.23338888 -0.5443213
## 6 0.06196503 0.02507901 0.9889015Betrachten wir Vertragskomplexität und BMI im Plot fällt auf, dass hohe Vertragskomplexität scheinbar eine notwendige Bedingung5 für hohe BMI darstellt.
plot(fscores$Vertrag,fscores$BMI, xlab="Vertragskomplexität", ylab="Business Modell Innovation")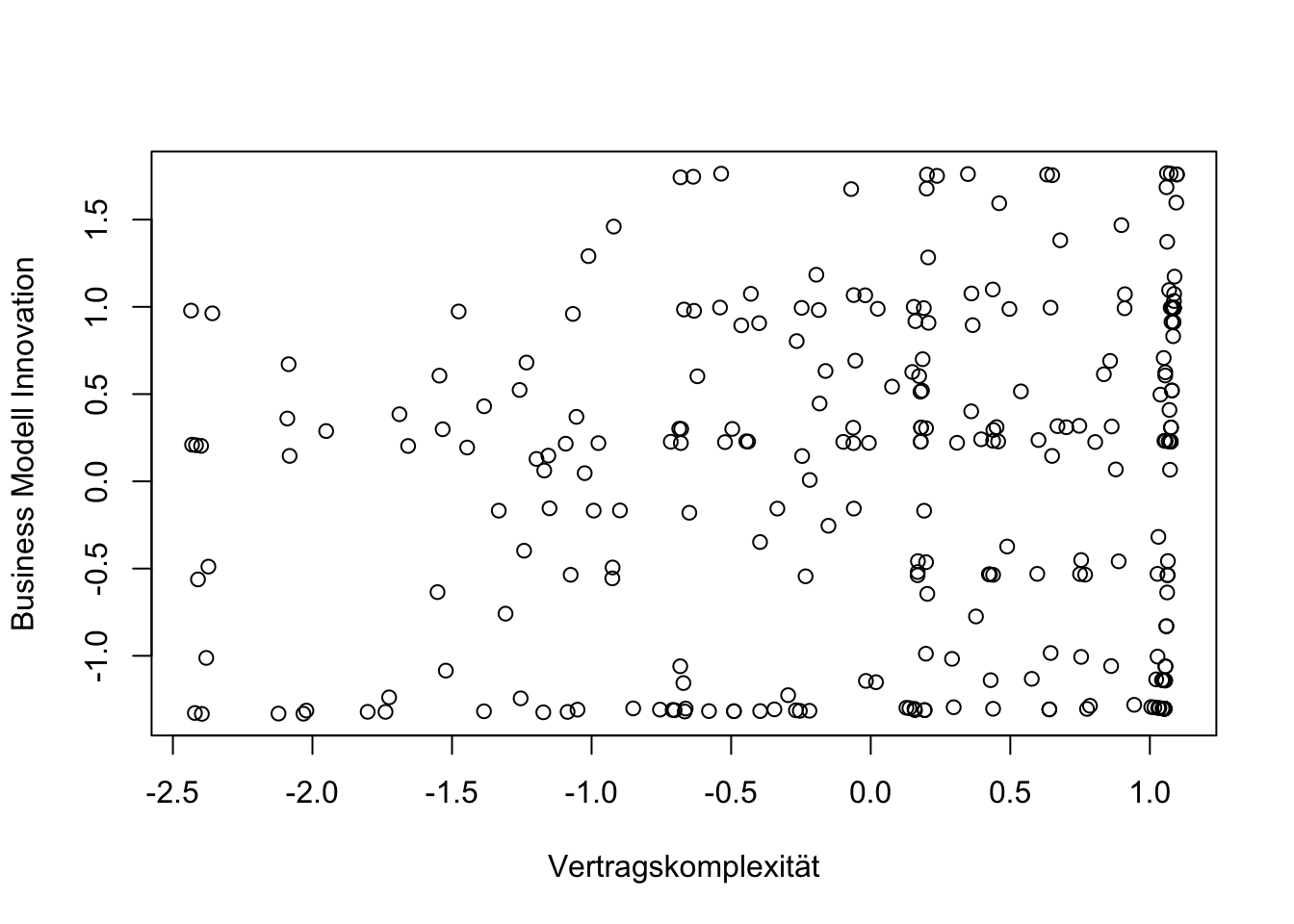
Die notwendige Bedingung (‘necessary condition’) ist ein Begriff aus der Logik, der beinhaltet, dass wir keine sehr hoch ausgeprägten Ergebnisse (hier BMI) vorfinden, ohne dass auch die Bedingung (hier Vertragskomplexität) in sehr hoher Ausprägung vorliegt.
Anders formuliert, links wo die Vertragskomplexität sehr gering ist, sind keine extrem hohen Werte von BMI zu finden. Andererseits sehen wir auch, dass die BMI bei extrem hoher Vertragskomplexität (rechts) in vielen Fällen nur sehr gering ist.
Hohe Vertragskomplexität ist demnach also keine hinreichende Bedingung (sufficient condition) die zwangsläufig mit hoher BMI einhergeht (überprüfen).
4.1 Beispiel 4: Prinzipal-Agenten-Theorie
vgl. Jensen & Meckling (1976); Jensen (2000)
Als Grundlage für unsere Hypothesenbildung greifen wir an dieser Stelle auf die Prinzipal-Agenten-Theorie zurück. Demnach können die Beziehungen zwischen Auftraggeber und Auftragnehmer durch eine asymmetrische Informationsverteilung beschrieben werden, die mit großer Unsicherheit gegenüber dem Vertragspartner einhergehen kann und diese Unsicherheit könnte möglicherweise dazu führen, dass die gewünschten Ergebnisse nicht erreicht werden (Jones & Bouncken, 2008, S. 106).
Vertragliche Kontrolle ist eine Möglichkeit, dem entgegen zu wirken (Jones & Bouncken, 2008, S. 106) und Verträge werden daher hinsichtlich ihrer Vollständigkeit unterschieden. Nehmen wir zusätzlich an, dass ein vollständiger Vertrag mehr Spezifikationen einschließt, um Unsicherheiten zwischen den Vertragspartnern zu reduzieren, wäre anzunehmen, dass ein vollständiger Vertrag in Hinblick auf seinen Umfang komplexer ausfällt und dazu beiträgt, Unsicherheiten zu reduzieren und Vertrauen in den Partnern zu fördern. Geprüft werden sollen demnach die Hypothesen:
Hypothese 1: “Vertragskomplexität fördert die Wertschöpfung für BMI” und
Hypothese 2: “Vertragskomplexität fördert interorganisationsales Vertrauen”.
Wir könnten in diesem Fall zwei einfache Regressionen durchführen. Das Ergebnis zeigt auf, dass der Zusammenhang zwischen Vertragskomplexität und BMI durch einen signifikant positiven Regressionskoeffizienten in Höhe von 0.123 unterstütz wird.
regression <- lm(BMI~Vertrag, data=fscores)
summary(regression)##
## Call:
## lm(formula = BMI ~ Vertrag, data = fscores)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.4326 -1.0319 0.1805 0.7798 1.8291
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -7.427e-17 5.774e-02 0.000 1.0000
## Vertrag 1.230e-01 5.841e-02 2.106 0.0362 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9452 on 266 degrees of freedom
## Multiple R-squared: 0.0164, Adjusted R-squared: 0.0127
## F-statistic: 4.434 on 1 and 266 DF, p-value: 0.03617Für den Zusammenhang zwischen Vertragskomplexität und Vertrauen resultiert ein signifikant positiver Regressionskoeffizient in Höhe von 0.195.
regression <- lm(Vertrauen~Vertrag, data=fscores)
summary(regression)##
## Call:
## lm(formula = Vertrauen ~ Vertrag, data = fscores)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.7688 -0.3339 0.0847 0.4095 0.9861
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.454e-16 3.509e-02 0.000 1
## Vertrag 1.953e-01 3.550e-02 5.503 8.78e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5744 on 266 degrees of freedom
## Multiple R-squared: 0.1022, Adjusted R-squared: 0.09883
## F-statistic: 30.28 on 1 and 266 DF, p-value: 8.777e-08Die Ergebnisse dieser zwei Regressionsanalysen wollen wir jetzt mit den Ergebnissen eines Strukturgleichungsmodells vergleichen.
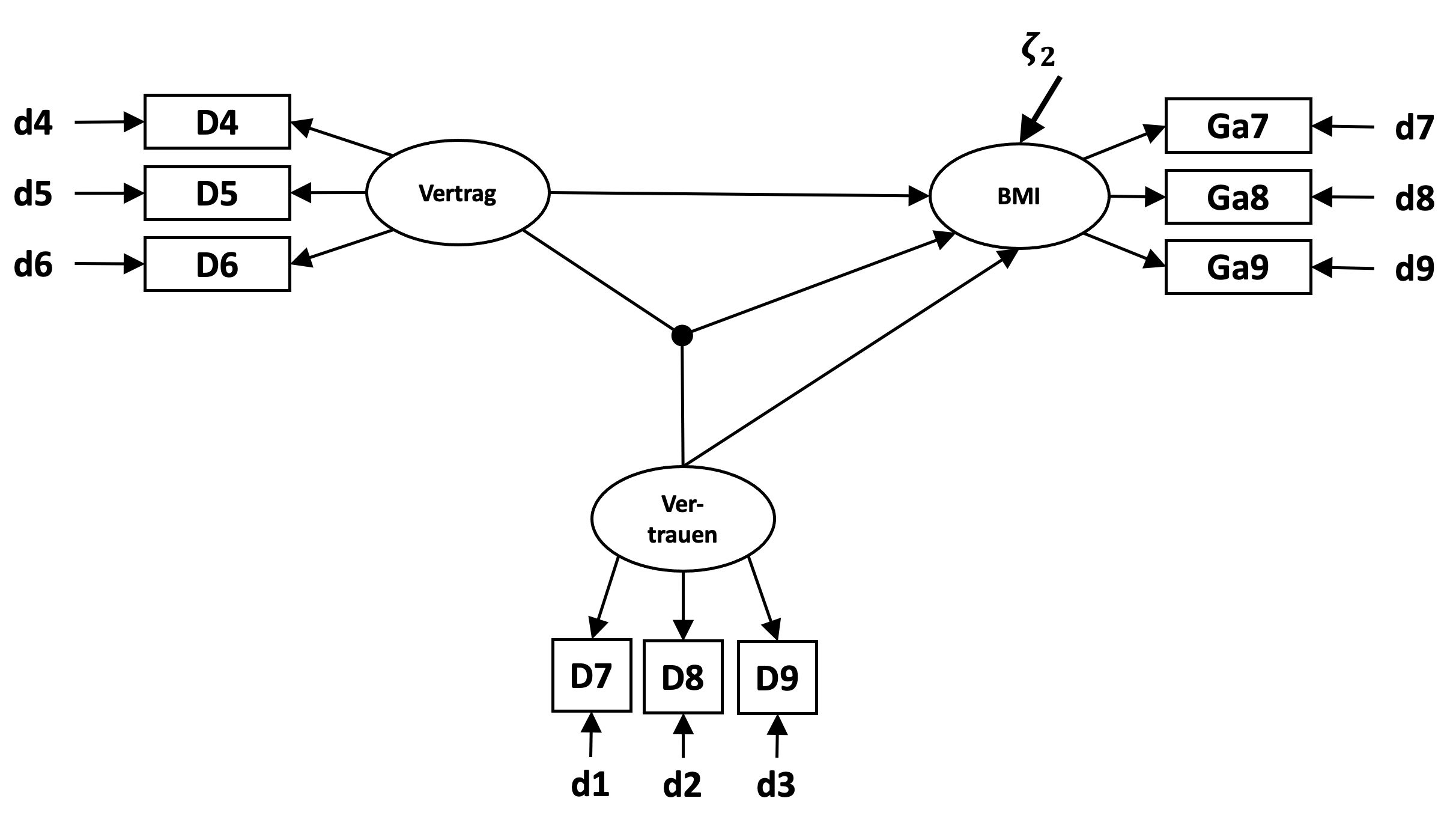
Die Abbildung zeigt das Modell mit einer exogenen latenten Variable (Vertragskomplexität) und zwei endogenen latenten Variablen (Vertrauen und Wertschöpfung) auf.
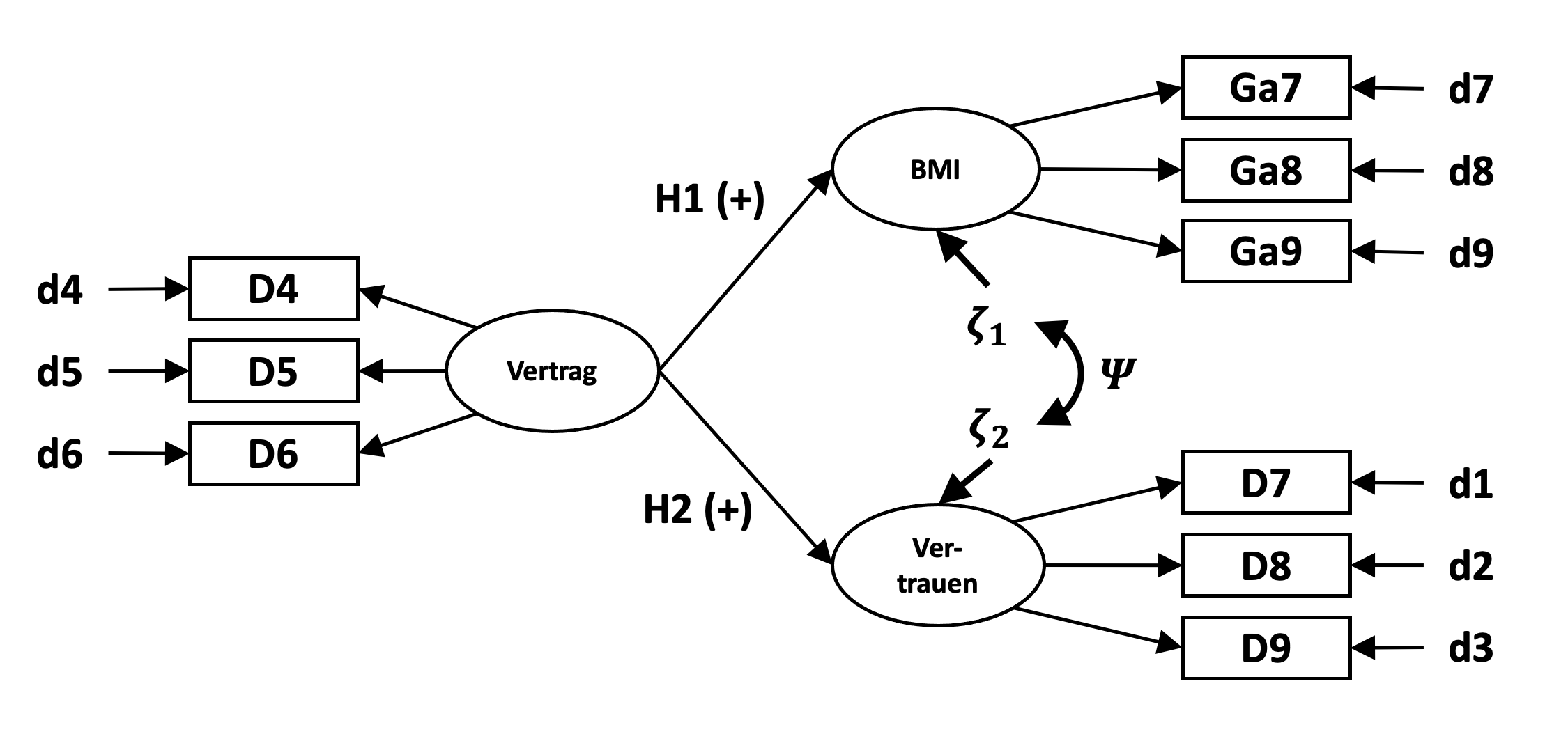
Wenn wir an dieser Stelle von exogenen Variablen sprechen, meinen wir möglicherweise Ursachen, können aber hinsichtlich des Studiendesign (Querschnitt) keine zeitliche Abfolge nachweisen.
Wir müssen also damit argumentieren, dass in dieser retrospektiven Befragung dem Befragten aufgrund der Formulierung der Aussagen des Befragungsinstrumentes deutlich wird, dass sich die Vertragskomplexität auf den Zeitraum zu Beginn der Kooperation bezieht, während sich die Aussagen zum Vertrauen auf eine Bewertung bezieht, die sich erst im weiteren Verlauf der Kooperation, und damit auch aufgrund primärer vertraglicher Festlegungen und darauffolgender Erfahrungen ergeben hat.
Überprüft wird demnach keine empirische Kausalrichtung, sondern die Annahme der Prinzipal-Agenten-Theorie.
4.2 Modell-Syntax
Ausgehend von den Modellspezifikation der konfirmatorischen Faktorenanalyse werden in diesem Hypothesenmodell demnach die Doppelpfeile zwischen Vertrag und Wertschöpfung sowie zwischen Vertrag und Vertrauen durch gerichtete Pfeile ersetzt.
Zusätzlich weisen die endogenen latenten Variablen Wertschöpfung für BMI sowie Vertrauen jeweils einen Varianzanteil auf der nicht durch das Modell erklärt wird und hier mit \(\zeta_1\) und \(\zeta_2\) bezeichnet ist. Die Kovarianz \(\Psi\) dieser nicht erklärten Varianzanteile wird im Strukturgleichungsmodell ebenfalls geschätzt.
In der Modell-Syntax werden anstelle der Doppel-Tilde für Kovarianzen nur einfache Tilden für die Regressionspfade von Vertrag auf BMI und Vertrag auf Vertrauen formuliert. Zu beachten ist, dass die zu erklärende Variable dabei vor der Tilde steht.
# Vollständiges Strukturgleichungsmodell
Model1 <- '
Vertrag =~ D4 + D5 + D6
Vertrauen =~ D7 + D8 + D9
BMI =~ Ga7 + Ga8 + Ga9
BMI ~ Vertrag
Vertrauen ~ Vertrag
Vertrauen ~~ BMI
'#Modellparameter anhand der Daten ermitteln
Model1_FIT <- sem(Model1,subdata)Betrachten wir zunächst wieder die globalen Güte-Kriterien des Modells. Aufgrund fehlender Werte wurden von den 423 Fällen nur 268 Fälle verwendet. Das insignifikante chi2 in Höhe von 25.677 weist auf eine gute Übereinstimmung zwischen theoretischer und empirischer Kovarianzmatrix hin.
# Ausgabe aller Model-Fit-Indizes zur Bestimmung der Modell-Güte
summary (Model1_FIT, fit.measures=TRUE)## lavaan 0.6-10 ended normally after 32 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
##
## Number of observations 268
##
## Model Test User Model:
##
## Test statistic 25.677
## Degrees of freedom 24
## P-value (Chi-square) 0.370
##
## Model Test Baseline Model:
##
## Test statistic 1438.390
## Degrees of freedom 36
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.999
## Tucker-Lewis Index (TLI) 0.998
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3037.526
## Loglikelihood unrestricted model (H1) -3024.687
##
## Akaike (AIC) 6117.051
## Bayesian (BIC) 6192.462
## Sample-size adjusted Bayesian (BIC) 6125.879
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.016
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.053
## P-value RMSEA <= 0.05 0.928
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.031
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Vertrag =~
## D4 1.000
## D5 1.117 0.063 17.816 0.000
## D6 0.941 0.060 15.657 0.000
## Vertrauen =~
## D7 1.000
## D8 1.166 0.094 12.350 0.000
## D9 1.276 0.104 12.253 0.000
## BMI =~
## Ga7 1.000
## Ga8 1.265 0.082 15.353 0.000
## Ga9 1.214 0.079 15.284 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BMI ~
## Vertrag 0.112 0.063 1.784 0.074
## Vertrauen ~
## Vertrag 0.180 0.044 4.127 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## .Vertrauen ~~
## .BMI -0.060 0.042 -1.424 0.154
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .D4 0.374 0.051 7.293 0.000
## .D5 0.274 0.055 4.994 0.000
## .D6 0.540 0.059 9.197 0.000
## .D7 0.386 0.041 9.494 0.000
## .D8 0.177 0.034 5.142 0.000
## .D9 0.311 0.046 6.780 0.000
## .Ga7 0.797 0.076 10.510 0.000
## .Ga8 0.208 0.054 3.875 0.000
## .Ga9 0.267 0.052 5.141 0.000
## Vertrag 1.078 0.128 8.451 0.000
## .Vertrauen 0.385 0.060 6.373 0.000
## .BMI 0.952 0.138 6.919 0.000Während zwei einzelne Regressionen beide Hypothesen angenommen hätten, würde die Prüfung im Strukturgleichungsmodell die erste Hypothese zurückweisen, zumindest, wenn im Vorfeld ein Kriterium von p < 0.05 festgelegt wurde.
Dies ist einer der nicht seltenen Fälle in denen das Strukturgleichungsmodell durch seine höhere Strenge eine Hypothese zurückweist, die mittels Regressionsmodell angenommen werden könnte.
Zurückzuführen ist dies in diesem Fall wahrscheinlich darauf, dass die Signifikanz von Koeffizienten im Strukturmodell anhand der z-Verteilung geprüft wird, während der Koeffizient bei der Regression anhand der t-Verteilung geprüft wird.
Die t-Verteilung weist in kleinen Stichproben eher ein signifikanten p-Wert auf, was aber auch eher zur Annahme einer falschen Hypothese führt. In diesem Fall wäre eine gangbare Lösung, den im Strukturmodell geschätzten Pfadkoeffizienten mit einem p-Wert < 0.10 als tendenziell signifikant zu bezeichnen und die Hypothese ebenfalls, aber unter Vorbehalt anzunehmen.
Ergebnisse aus zwei Regressionen:
\(\beta_1\)=0.12; t=2.11; p=0.036
\(\beta_2\)=0.20; t=5.60; p=0.000
Ergebnisse aus einem SEM:
\(\gamma_1\)=0.11; z=1.78; p=0.074
\(\gamma_2\)=0.18; z=4.13; p=0.000
4.3 Indirekte Pfade
Tendenziell werden wirtschaftswissenschaftliche Untersuchungen seltener darauf ausgerichtet sein, Vertrauen als Ergebnisvariable zu betrachten, sondern sie als Kontingenz also als mögliche Begleiterscheinung betrachten.
Zudem wäre es im Kontext der anfänglich angesprochenen Prinzipal-Agenten-Theorie interessant, inwiefern Vertrauen für den Zusammenhang zwischen Vertragskomplexität und Wertschöpfung bedeutsam ist.
Bedeutsam könnte in diesem Zusammenhang bezeichnen, dass ein großer Teil des positiven Zusammenhangs zwischen Vertragskomplexität und Wertschöpfung durch Vertrauen erklärt werden könnte. Aus den bereits besprochenen Konzepten entspricht dies der Mediation bzw. dem indirekten Effekt.
Wir positionieren die Variable des Vertrauens im Modell zwischen Vertragskomplexität und der endogenen latenten Variable BMI.
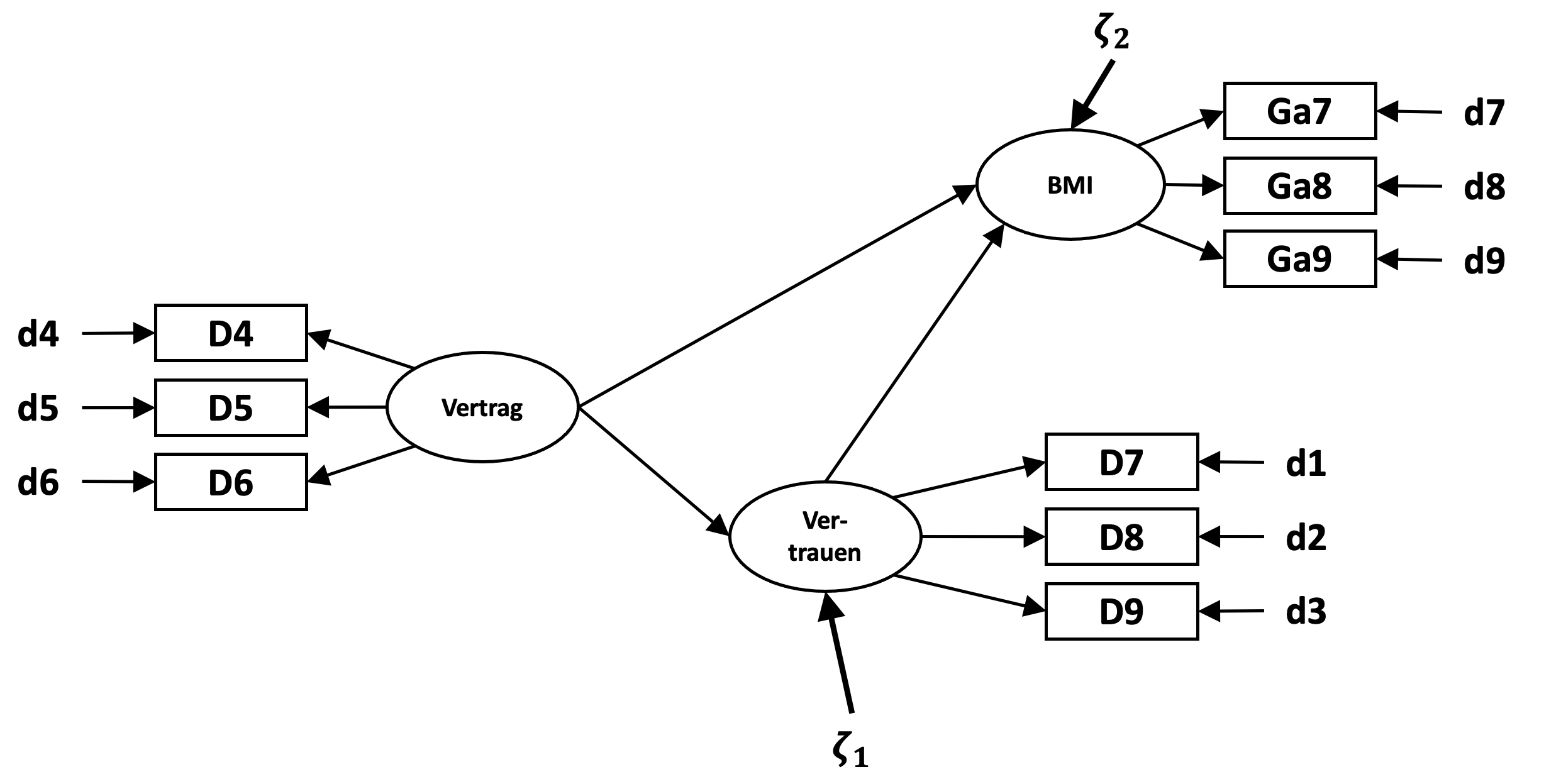
Über die bereits angesprochene Fragestellung, zu welchem Anteil der Zusammenhang zwischen Vertragskomplexität und BMI durch Vertrauen erklärt werden kann, wird auch deutlich, welcher Zusammenhang zwischen Vertrag und BMI wäre zu erwarten, wenn der Zusammenhang zwischen Vertragskomplexität und Wertschöpfung für Businessmodellinnovation nicht über Variationen des Vertrauens in den Partner erklärt wird.
Vertragskomplexität, welche nicht darauf ausgerichtet ist, das Vertrauen in den Kooperationspartner zu fördern, könnte andere Bereiche der Austauschbeziehung zwischen Kooperationspartner betreffen, z.B. Details über Verwertungsrechte, Liefer- oder Abnahmegarantien oder formale Rahmenbedingungen, welche die Interaktion zwischen den Kooperationspartnern regulieren und insbesondere vor dem Hintergrund innovativer Vorhaben begrenzend oder behindernd wirken könnten.
Wie wir es schon in Pfadmodellen gezeigt hatten, ergibt sich in solch einem Modell der Totale Effekt als Summe des direkten und des totalen indirekten Effektes, wobei sich der totale indirekte Effekt aus dem Produkt der Pfadkoeffizienten ergibt.
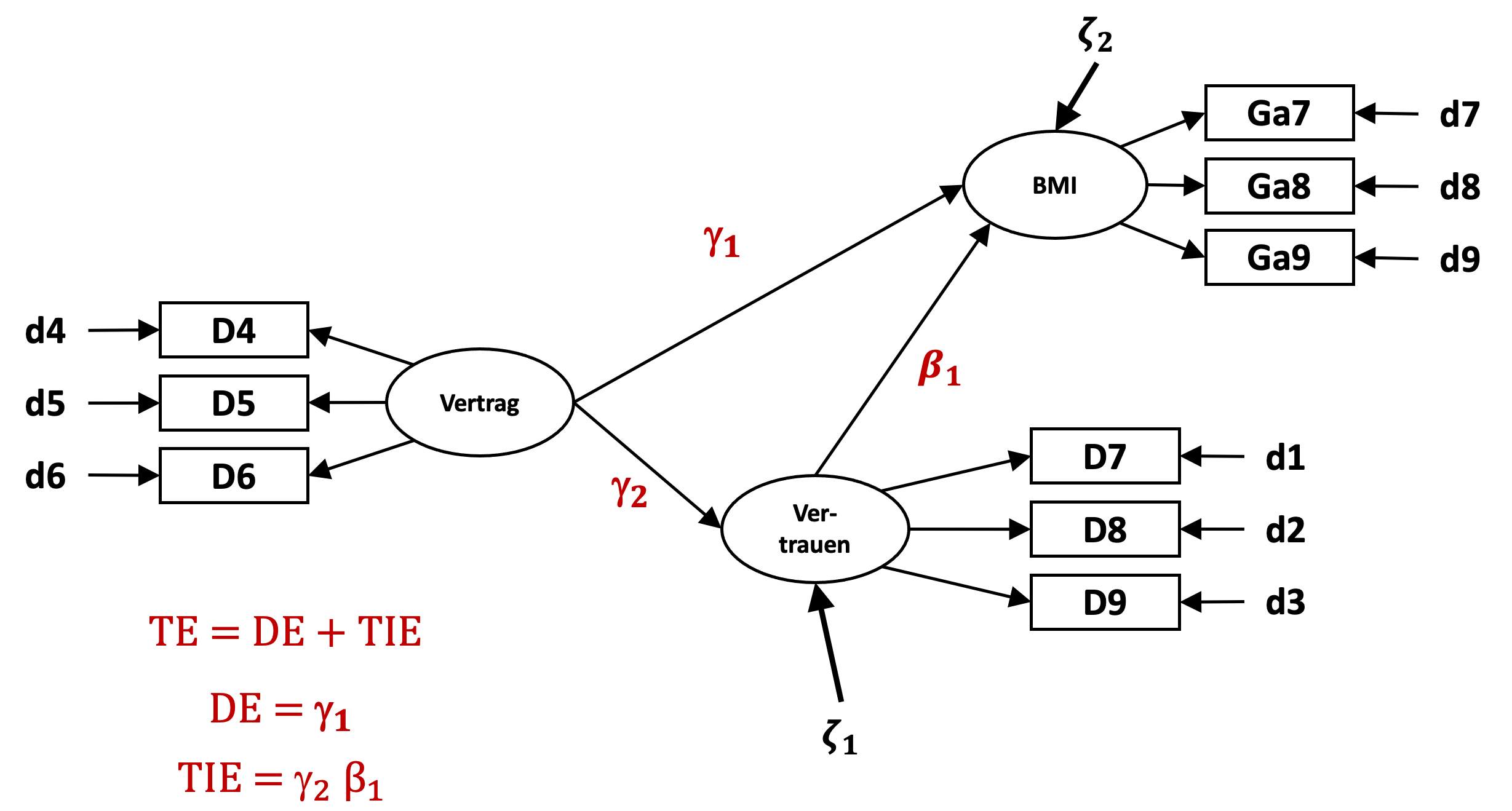
In der Modellspezifikation ersetzen wir die Doppeltilde, welche die Kovarianz von Vertrag und Vertrauen bezeichnete durch eine einzelne Tilde, um sie als gerichteten Pfad zu definieren.
# Vollständiges Strukturgleichungsmodell mit indirektem Pfad
Model2 <- '
Vertrag =~ D4 + D5 + D6
Vertrauen =~ D7 + D8 + D9
BMI =~ Ga7 + Ga8 + Ga9
BMI ~ gamma1*Vertrag
Vertrauen ~ gamma2*Vertrag
BMI ~ beta1*Vertrauen
DE:=gamma1
TIE:=gamma2*beta1
TE:=DE+TIE
'Außerdem weisen wir den drei interessierenden Pfadkoeffizienten jeweils ein Label zu. wir bezeichnen sie als ‘gamma1’, ‘gamma2’ und ‘beta1’, und definieren die Gleichungen für den Totalen Effekt als Summe des direkten und des totalen indirekten Effektes, wobei der direkte Effekt gleich dem Pfadkoeffizienten ‘gamma1’ ist und der Totale indirekte Effekt sich aus dem Produkt von ‘gamma2’ und ‘beta1’ ergibt.
#Modellparameter anhand der Daten ermitteln
Model2_FIT <- sem(Model2,subdata)Wir beginnen wieder mit der Bewertung der globalen Modell-Güte- Kriterien. Von den 423 Befragungen sind 268 zur Bestimmung verwendet worden. Aus dem chi2-Wert von 25.677 resultiert bei den gegebenen 24 Freiheitsgraden ein p-Wert in Höhe von 0.370. Dies weist darauf hin, das keine signifikante Abweichung zwischen der theoretischen und der empirischen Kovarianzmatrix vorliegt.
Der CFI liegt mit einem Wert von 0.999 deutlich über dem geforderten Wert von 0.95. Ebenso der RMSEA. Er liegt mit einem Wert von 0.016 deutlich unter dem kritischen Wert von 0.06, wie auch der SRMR, der mit einem Wert von 0.031 unter dem kritischen Wert von 0.08 liegt.
# Ausgabe aller Model-Fit-Indizes zur Bestimmung der Modell-Güte
summary (Model2_FIT, fit.measures=TRUE)## lavaan 0.6-10 ended normally after 32 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
##
## Number of observations 268
##
## Model Test User Model:
##
## Test statistic 25.677
## Degrees of freedom 24
## P-value (Chi-square) 0.370
##
## Model Test Baseline Model:
##
## Test statistic 1438.390
## Degrees of freedom 36
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.999
## Tucker-Lewis Index (TLI) 0.998
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3037.526
## Loglikelihood unrestricted model (H1) -3024.687
##
## Akaike (AIC) 6117.051
## Bayesian (BIC) 6192.462
## Sample-size adjusted Bayesian (BIC) 6125.879
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.016
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.053
## P-value RMSEA <= 0.05 0.928
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.031
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Vertrag =~
## D4 1.000
## D5 1.117 0.063 17.816 0.000
## D6 0.941 0.060 15.657 0.000
## Vertrauen =~
## D7 1.000
## D8 1.166 0.094 12.350 0.000
## D9 1.276 0.104 12.253 0.000
## BMI =~
## Ga7 1.000
## Ga8 1.265 0.082 15.353 0.000
## Ga9 1.214 0.079 15.284 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BMI ~
## Vertrag (gmm1) 0.140 0.066 2.112 0.035
## Vertrauen ~
## Vertrag (gmm2) 0.180 0.044 4.127 0.000
## BMI ~
## Vertran (bet1) -0.155 0.108 -1.434 0.152
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .D4 0.374 0.051 7.293 0.000
## .D5 0.274 0.055 4.994 0.000
## .D6 0.540 0.059 9.197 0.000
## .D7 0.386 0.041 9.494 0.000
## .D8 0.177 0.034 5.142 0.000
## .D9 0.311 0.046 6.780 0.000
## .Ga7 0.797 0.076 10.510 0.000
## .Ga8 0.208 0.054 3.875 0.000
## .Ga9 0.267 0.052 5.141 0.000
## Vertrag 1.078 0.128 8.451 0.000
## .Vertrauen 0.385 0.060 6.373 0.000
## .BMI 0.943 0.136 6.910 0.000
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## DE 0.140 0.066 2.112 0.035
## TIE -0.028 0.021 -1.357 0.175
## TE 0.112 0.063 1.784 0.074Betrachten wir zunächst die Pfadkoeffizienten. Der Pfad von Vertragskomplexität auf Wertschöpfung für BMI, wir hatten ihm das Label gamma1 zugewiesen, beträgt 0.14 und dies ist mit einem korrespondierenden p-Wert in Höhe von 0.035 signifikant unterschiedlich von null.
Ähnliches sehen wir für den Pfad von Vertragskomplexität auf das Vertrauen in den Kooperationspartner. Wir haben ihn mit ‘gamma2’ bezeichnet. ’gamma2Ä beträgt 0.180 und ist mit einem p-Wert kleiner als 0.001 höchst signifikant.
Allein der Pfadkoeffizient von Vertrauen auf Wertschöpfung für BMI stellt sich als insignifikant heraus.
Welche Konsequenzen hat dies nun für unsere definierten Parameter des totalen und des totalen indirekten Effektes .
Der direkte Effekt entspricht ja dem Pfad ‘gamma1’. Das ist also der identische Wert wie oben.
Der totale indirekte Effekt von Vertragskomplexität über Vertrauen auf die Wertschöpfung für BMI, also das Produkt von ‘gamma2’ und ‘beta1’, ist nicht signifikant.
Und der totale Effekt von Vertragskomplexität auf Wertschöpfung BMI ist gleich 0.11, insignifikant oder tendenziell signifikant mit einem p-Wert von 0.074. Das ist im übrigen das gleiche Ergebnis, welches wir im ersten Modell für Vertragskomplexität erzielt haben, als Vertrauen als abhängige Variable untersucht wurde.
4.4 Interaktion
Im letzten Abschnitt wurde gezeigt, dass Vertragskomplexität nicht nur die Wertschöpfung für BMI in Kooperationen, sondern auch das Vertrauen in den Kooperationspartner fördern kann. In einem zweiten Modell konnte nicht gezeigt werden, dass das Vertrauen in den Kooperationspartner den Einfluss von Vertragskomplexität auf BMI erklären kann, also dass das Vertrauen ein Mediator für den Zusammenhang zwischen Vertragskomplexität und BMI darstellt.
Ich hatte erwähnt, dass es an dieser Stelle keine Erklärung der Kausalitäten geben kann, weil wir in dem Querschnittdesign nur von der Annahme der Prinzipal-Agenten-Theorie ausgehen können, dass vertragliche Komplexität zur Reduzierung von Unsicherheit eingesetzt wird und demnach unter anderem Vertrauen in den Kooperationspartner fördern kann.
Die zurückgewiesene Mediationshypothese weist insofern darauf hin, dass die Prinzipal Agenten-Theorie in diesem Kontext nicht alle Befunde so gut vorhersagen kann.
4.5 Beispiel 5: Relational contracting/ Relational view
vgl. Williamson (1985); Gulati (1998); Bouncken et al. (2020)
Eine andere Perspektive bietet eine relationale Sichtweise, wonach Vertrauen die Komplexität von Verträgen substituieren kann (Bouncken, Hughes, Ratzmann, Cesinger & Pesch, 2020). Es wäre also vorstellbar, dass eine Interaktion zwischen Vertragskomplexität und Vertrauen existiert.
Hypothese 1: “Vertragskomplexität und Vertrauen interagieren in Hinsicht auf die Wertschöpfung für BMI.”
Hypothese 2: “Der positive Einfluss der Vertragskomplexität auf die Wertschöpfung für BMI ist bei geringem Vertrauen ausgeprägter als bei hohem Vertrauen.”
Dabei würde sich die zweite Hypothese auf den speziellen Fall beziehen, der auch schon von der Prinzipal Agenten Theorie angesprochen wurde. Wenn nur sehr geringes Vertrauen in den Kooperationspartner besteht, werden komplexere Verträge notwendig und möglicherweise erfolgversprechend sein. Voraussetzung für den Nachweis einer solchen Moderation ist grundlegend die Signifikanz dieser Interaktion.
Die Darstellung der Interaktion von latenten Variablen unterscheidet sich im Prinzip nicht von denen, wie sie in den ersten Kapiteln für die Regressionen und Pfadmodelle aufgezeigt wurde.
Auch die Operationalisierung der Interaktionsterme durch mittelwertzentrierte Produktterme ist übertragbar. Da für die latenten Variablen vor der Modelltestung jedoch keine Werte existieren, erfordert das Verfahren kurze Anmerkungen.
Dabei werde ich zwei Möglichkeiten aufzeigen, wobei die erste eine stark vereinfachte Version der zweiten ist. Für Modellierungen im Rahmen der studentischen Forschung ist die erste jedoch völlig ausreichend.
Aufbauend auf der bekannten konfirmatorischen Faktorenanalyse für Vertragskomplexität, Vertrauen und Wertschöpfung für BMI betrachten wir in diesem Fall das Modell mit den zwei exogenen latenten Variablen ‘Vertragskomplexität’ und ‘Vertrauen’ und einer endogenen latenten Variable ‘BMI’ vorerst ohne Interaktion.
Den gesamten Code für das Modell habe ich hier schon vorbereitet. Zuerst werden wir wieder die Datei mit den Daten einlesen und die interessierenden Indikatoren der Datenmatrix ‘subdata’ zuordnen.
#Einlesen von .CSV-Tabellen mit Spaltennamen
data <- read.csv2(file='_bookdown_files/data/DatenSS20_21.csv',
header=TRUE)
subdata <- data [,c("D4","D5","D6","D7","D8","D9","Ga7","Ga8","Ga9")]
head(subdata)## D4 D5 D6 D7 D8 D9 Ga7 Ga8 Ga9
## 1 2 2 2 4 4 4 1 2 2
## 2 4 4 4 4 4 4 4 3 3
## 3 NA NA NA NA NA NA NA NA NA
## 4 4 4 4 4 5 4 4 3 3
## 5 4 4 4 3 3 3 4 4 4
## 6 5 5 5 5 5 5 NA NA NAEin Blick auf die Datenmatrix zeigt uns, dass auch Fälle vorhanden sind, in denen einzelne oder alle Werte fehlen.
Wir laden die Programm-Bibiothek ‘Lavaan’ und spezifizieren das Modell mit den drei latenten Variablen, wobei Vertragskomplexität und Vertrauen als exogene und Wertschöpfung für BMI als endogene Variablen bestimmt werden.
library ('lavaan')
Model1 <- '
Vertrag =~D4 + D5 + D6
Vertrauen =~ D7 + D8 + D9
BMI =~ Ga7 + Ga8 + Ga9
BMI ~ Vertrag + Vertrauen
'Wir führen den Schätz-Algorithmus aus und sehen uns die Ergebnisse der Schätzung an. Von den insgesamt 423 Fällen werden 268 in die Schätzung einbezogen. Die übrigen weisen fehlende Werte auf.
Model1_FIT <- sem(Model1,subdata)
summary (Model1_FIT, fit.measures=TRUE)## lavaan 0.6-10 ended normally after 32 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
##
## Used Total
## Number of observations 268 423
##
## Model Test User Model:
##
## Test statistic 25.677
## Degrees of freedom 24
## P-value (Chi-square) 0.370
##
## Model Test Baseline Model:
##
## Test statistic 1438.390
## Degrees of freedom 36
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.999
## Tucker-Lewis Index (TLI) 0.998
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3037.526
## Loglikelihood unrestricted model (H1) -3024.687
##
## Akaike (AIC) 6117.051
## Bayesian (BIC) 6192.462
## Sample-size adjusted Bayesian (BIC) 6125.879
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.016
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.053
## P-value RMSEA <= 0.05 0.928
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.031
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Vertrag =~
## D4 1.000
## D5 1.117 0.063 17.816 0.000
## D6 0.941 0.060 15.657 0.000
## Vertrauen =~
## D7 1.000
## D8 1.166 0.094 12.350 0.000
## D9 1.276 0.104 12.253 0.000
## BMI =~
## Ga7 1.000
## Ga8 1.265 0.082 15.353 0.000
## Ga9 1.214 0.079 15.284 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BMI ~
## Vertrag 0.140 0.066 2.112 0.035
## Vertrauen -0.155 0.108 -1.434 0.152
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## Vertrag ~~
## Vertrauen 0.194 0.050 3.887 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .D4 0.374 0.051 7.293 0.000
## .D5 0.274 0.055 4.994 0.000
## .D6 0.540 0.059 9.197 0.000
## .D7 0.386 0.041 9.494 0.000
## .D8 0.177 0.034 5.142 0.000
## .D9 0.311 0.046 6.780 0.000
## .Ga7 0.797 0.076 10.510 0.000
## .Ga8 0.208 0.054 3.875 0.000
## .Ga9 0.267 0.052 5.141 0.000
## Vertrag 1.078 0.128 8.451 0.000
## Vertrauen 0.420 0.065 6.422 0.000
## .BMI 0.943 0.136 6.910 0.000Der insignifikante chi2-Test weist darauf hin, dass die theoretische Kovarianzmatrix unseres Modells nicht signifikant von der empirischen Datenmatrix abweicht.
Der CFI weist mit einem Wert größer als 0.95 und der RMSEA mit einem Wert kleiner als 0.06 auf eine gute Anpassungsgüte des Modells hin.
Mit einem Wert kleiner als 0.08 weist der SRMR ebenfalls auf ein gutes Modell hin.
Wir finden in diesem Modell einen signifikant positiven Pfadkoeffizienten für Vertragskomplexität auf Wertschöpfung für BMI. Der Pfadkoeffizient von Vertrauen in den Kooperationspartner ist insignifikant.
Das repliziert insofern das Mediationsmodell, als dass wir auch dort keinen signifikanten Pfadkoeffizienten von Vertrauen auf Wertschöpfung für BMI vorgefunden hatten. (Prüfen)
Im zweiten Modell wollen wir nun den Interaktionsterm einbeziehen. Kenny & Judd (1984) haben eine Methode vorgestellt, mit welcher ein latenter Interaktionsterm bestimmt werden kann, indem das Produkt der Indikatoren der interagierenden latenten Variablen als Indikatoren des Interaktionsterms eingesetzt werden (Kenny & Judd, 1984).
Dabei hat sich herausgestellt, dass es wie auch bei Interaktionstermen für Regressionen von Vorteil ist, diese Indikatoren vor der Produktbildung zu zentrieren.
Dazu zieht man in der Datenmatrix für jeden Indikator in jedem einzelnen Fall den Spaltenweisen Mittelwert ab. Da die spaltenweisen Mittelwerte in den Grundeinstellungen von ‘R’ nicht berechnet werden, wenn fehlende Werte in dieser Spalte vorhanden sind, werde ich zuerst nur diejenigen Datenzeilen behalten, die auch vollständig ausgefüllt sind, d.h. keine fehlenden Werte aufweisen.
subdata <- subdata[complete.cases(subdata),] Im nächsten Schritt bestimme ich hier einmal den spaltenweisen Mittelwert des Indikators ‘D4’.
mean (subdata$D4) ## [1] 3.865672In den folgenden Zeilen mit ‘R’-Code ziehe ich nun jeweils den Spaltenweisen Mittelwert von den Skalenwerten ab, bevor ich das Produkt bilde aus dem mittelwertzentrierten Skalenwert des ersten Indikators für Vertragskomplexität mit dem mittelwertzentrierten Skalenwert des ersten Indikators von Vertrauen. Es ist wichtig, hier diese Klammern zu setzen, damit die Differenz vor der Produktbildung berechnet wird. Anderenfalls erhalten wir falsche Indikatorwerte für den Interaktionsterm.
subdata$i1 <- (subdata$D4-mean(subdata$D4)) * (subdata$D7-mean(subdata$D7))
subdata$i2 <- (subdata$D5-mean(subdata$D5)) * (subdata$D8-mean(subdata$D8))
subdata$i3 <- (subdata$D6-mean(subdata$D6)) * (subdata$D9-mean(subdata$D9))Die drei neu erstellten Variablen, ich habe sie mit i1, i2 und i3 benannt, liegen jetzt in der Datenmatrix ‘subdata’ vor und können im folgenden Modell verwendet werden, um die latente Interaktion von Vertragskomplexität und Vertrauen zu spezifizieren.
head (subdata) ## D4 D5 D6 D7 D8 D9 Ga7 Ga8 Ga9 i1 i2 i3
## 1 2 2 2 4 4 4 1 2 2 0.27845845 0.52553464 0.19881934
## 2 4 4 4 4 4 4 4 3 3 -0.02004901 -0.07894297 -0.02506126
## 4 4 4 4 4 5 4 4 3 3 -0.02004901 0.18225106 -0.02506126
## 5 4 4 4 3 3 3 4 4 4 -0.15437737 -0.34013700 -0.24894186
## 8 4 3 4 4 4 5 2 2 2 -0.02004901 0.22329583 0.19881934
## 9 4 4 3 4 4 5 4 4 4 -0.02004901 -0.07894297 -0.68924037Im Modell ändern wir einzig eine Zeile Code im Messmodell, in der wir die latente Variable ‘Interaktion’ benennen und ihr die drei Indikatoren i1, i2 und i3 zuweisen. Im Strukturmodell erweitern wir die Funktion zur Prognose von Wertschöpfung für BMI durch die benannte latente Variable ‘Interaktion’.
Model2 <- '
Vertrag =~ D4 + D5 + D6
Vertrauen =~ D7 + D8 + D9
Interaktion =~ i1 + i2 + i3
BMI =~ Ga7 + Ga8 + Ga9
BMI ~ Vertrag + Vertrauen + Interaktion
'Wenn wir nun das Modell schätzen und die Ergebnisse anfordern, sehen wir wieder die üblichen Kriterien: wir haben 268 Fälle zur Schätzung verwendet, das Modell ist hinsichtlich chi2-Test insignifikant, d.h. es liegt eine gute Übereinstimmung zwischen theoretischer und empirischer Kovarianzmatrix vor, der CFI ist größer als 0.95, der RMSEA ist kleiner als 0.06 und der SRMR ist kleiner als 0.08.
Model2_FIT <- sem(Model2,subdata)
summary (Model2_FIT, fit.measures=TRUE)## lavaan 0.6-10 ended normally after 35 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 30
##
## Number of observations 268
##
## Model Test User Model:
##
## Test statistic 60.292
## Degrees of freedom 48
## P-value (Chi-square) 0.110
##
## Model Test Baseline Model:
##
## Test statistic 1691.111
## Degrees of freedom 66
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.992
## Tucker-Lewis Index (TLI) 0.990
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -4174.293
## Loglikelihood unrestricted model (H1) -4144.147
##
## Akaike (AIC) 8408.586
## Bayesian (BIC) 8516.315
## Sample-size adjusted Bayesian (BIC) 8421.197
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.031
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.053
## P-value RMSEA <= 0.05 0.917
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.037
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Vertrag =~
## D4 1.000
## D5 1.122 0.063 17.841 0.000
## D6 0.942 0.060 15.616 0.000
## Vertrauen =~
## D7 1.000
## D8 1.176 0.095 12.381 0.000
## D9 1.288 0.105 12.239 0.000
## Interaktion =~
## i1 1.000
## i2 1.313 0.174 7.538 0.000
## i3 1.452 0.188 7.709 0.000
## BMI =~
## Ga7 1.000
## Ga8 1.266 0.082 15.344 0.000
## Ga9 1.214 0.080 15.276 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BMI ~
## Vertrag 0.131 0.068 1.921 0.055
## Vertrauen -0.127 0.119 -1.072 0.284
## Interaktion 0.082 0.119 0.683 0.495
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## Vertrag ~~
## Vertrauen 0.192 0.049 3.882 0.000
## Interaktion 0.055 0.048 1.136 0.256
## Vertrauen ~~
## Interaktion -0.126 0.035 -3.613 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .D4 0.379 0.051 7.387 0.000
## .D5 0.267 0.055 4.888 0.000
## .D6 0.542 0.059 9.227 0.000
## .D7 0.392 0.041 9.614 0.000
## .D8 0.175 0.033 5.238 0.000
## .D9 0.308 0.045 6.869 0.000
## .i1 0.933 0.092 10.138 0.000
## .i2 0.340 0.076 4.449 0.000
## .i3 0.710 0.106 6.680 0.000
## .Ga7 0.797 0.076 10.513 0.000
## .Ga8 0.208 0.054 3.884 0.000
## .Ga9 0.266 0.052 5.130 0.000
## Vertrag 1.073 0.127 8.427 0.000
## Vertrauen 0.414 0.065 6.380 0.000
## Interaktion 0.407 0.094 4.319 0.000
## .BMI 0.940 0.136 6.906 0.000Im Ergebnis sehen wir, dass die Signifikanz des Pfadkoeffizienten von Vertragskomplexität auf Wertschöpfung für BMI im Vergleich zum Modell ohne Interaktion etwas gesunken ist, also auch in diesem Fall wie schon im Mediationsmodell erwähnt würde der Forschende vor der Frage stehen, ob der Pfad als tendenziell signifikant mit einem p-Wert kleiner als 0.10 oder als insignifikant mit einem p-Wert größer als 0.05 anzusehen ist. Nach wie vor hat Vertrauen einen insignifikanten Pfadkoeffizienten und die Interaktion ebenfalls.
Es liegt also keine Interaktion vor und die Frage nach der Moderation bedarf dem entsprechend keiner weiteren Nachforschungen.
4.6 Beispiel 6: Knowledge creation theory/ Socio-cognitive view
vgl. Nonaka, Byosiere, Borucki & Konno (1994); Bouncken, Pesch & Reuschl (2016); Bouncken et al. (2020)
Während die Wertschöpfung für BMI im letzten Modell stärker auf ein Ergebnis, bzw. seine subjektive Bewertung ausgerichtet war, möchte ich an dieser Stelle stärker auf eine prozessuale Perspektive der Kooperation zurückgreifen. Informationen und Wissen sind zentrale, produktive, strategische Ressourcen für Unternehmen. Und Wissen entsteht durch die Interaktionen zwischen Kooperationspartnern.
Nach Theorie der Wissensbildung von Nonaka et al. (1994) sind Externalisierung und Wissenskombination basale Formen der Wissensumwandlung, die zur Wissensbildung beitragen können. Aus einer sozio-kognitiven Sicht sind vertrauensvolle und intensive Interaktionen zwischen den Beteiligten grundlegende Bedingungen für die gemeinsame Wissensbildung (Bouncken et al., 2016; Bouncken et al., 2020).
Dies lässt die Annahmen zu, dass Wissenskombination und interorganisationales Vertrauen in Hinblick auf die gemeinsame Wissensbildung interagieren bzw. dass der Einfluss von Wissenskombination auf die gemeinsame Wissensbildung durch interorganisationales Vertrauen gefördert wird.
Hypothese 1: “Wissenskombination und Vertrauen interagieren in Hinsicht auf die gemeinsame Wissensbildung.”
Hypothese 2: “Der positive Einfluss der Wissenskombination auf die gemeinsame Wissensbildung wird durch interorganisationales Vertrauen gefördert.”
Beginnen werde ich an dieser Stelle mit der Auswahl den entsprechenden Indikatoren für Wissenskombination, interorganisationales Vertrauen und gemeinsame Wissensbildung. Die Zuordnung der Indikatoren zu den latenten Konstrukten wurde bereits an anderer Stelle in einer konfirmatorischen Faktorenanalyse überprüft, so dass ich an dieser Stelle nicht noch einmal darauf eingehen werde.
subdata3 <- data [,c("F1","F2","F3","D7","D8","D9","F4","F5","F6")] Die entsprechenden Indikatoren habe ich der Datenmatrix ‘subdata3’ zugewiesen. In der Spezifikation des ‘Lavaan’-Modells habe ich für die gemeinsame Wissensbildung die Bezeichnung ‘MKC’ verwendet, sie steht als Abkürzung für ‘Mutual knowledge creation’.
Model4 <- '
Kombi =~ F1 + F2 + F3
Vertrauen =~ D7 + D8 + D9
MKC =~ F4 + F5 + F6
MKC ~ Kombi + Vertrauen
'Die Annahmen, die in diesem Modell überprüft werden sind, dass Wissenskombination und interorganisationales Vertrauen auf die gemeinsame Wissensbildung wirken.
Model4_FIT <- sem(Model4,subdata3)
summary (Model4_FIT)## lavaan 0.6-10 ended normally after 30 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
##
## Used Total
## Number of observations 301 423
##
## Model Test User Model:
##
## Test statistic 52.269
## Degrees of freedom 24
## P-value (Chi-square) 0.001
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Kombi =~
## F1 1.000
## F2 1.064 0.076 13.916 0.000
## F3 1.009 0.077 13.126 0.000
## Vertrauen =~
## D7 1.000
## D8 1.198 0.091 13.097 0.000
## D9 1.310 0.102 12.864 0.000
## MKC =~
## F4 1.000
## F5 1.030 0.066 15.532 0.000
## F6 0.692 0.056 12.320 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## MKC ~
## Kombi 0.674 0.107 6.322 0.000
## Vertrauen 0.206 0.113 1.822 0.068
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## Kombi ~~
## Vertrauen 0.244 0.038 6.381 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .F1 0.311 0.037 8.454 0.000
## .F2 0.282 0.037 7.539 0.000
## .F3 0.382 0.042 9.147 0.000
## .D7 0.394 0.038 10.453 0.000
## .D8 0.155 0.029 5.400 0.000
## .D9 0.296 0.039 7.506 0.000
## .F4 0.473 0.059 7.976 0.000
## .F5 0.221 0.050 4.408 0.000
## .F6 0.542 0.050 10.782 0.000
## Kombi 0.533 0.069 7.692 0.000
## Vertrauen 0.389 0.059 6.635 0.000
## .MKC 0.638 0.084 7.593 0.000Das Ergebnis weist zunächst darauf hin, dass der geschätzte Pfadkoeffizienten für den Zusammenhang von Wissenskombination und gemeinsamer Wissensbildung die Annahme unterstützt, dass Wissenskombination die gemeinsame Wissensbildung fördert.
Der Zusammenhang zwischen interorganisationalen Vertrauen und gemeinsamer Wissensbildung ist mit einem p-Wert größer als 0.05 insignifikant bzw. er wäre tendenziell signifikant mit einem p-Wert kleiner als 0.10.
Um die Interaktion zwischen beiden latenten Variablen zu bestimmen, werde ich wieder nur die Fälle verwenden, welche keine fehlenden Werte aufweisen und die mittelwertzentrierten Indikatorprodukte berechnen.
subdata3 <- subdata3[complete.cases(subdata3),]
subdata3$i1 <- (subdata3$F1-mean(subdata3$F1)) *
(subdata3$D7-mean(subdata3$D7))
subdata3$i2 <- (subdata3$F2-mean(subdata3$F2)) *
(subdata3$D8-mean(subdata3$D8))
subdata3$i3 <- (subdata3$F3-mean(subdata3$F3)) *
(subdata3$D9-mean(subdata3$D9))Die mittelwertzentrierten Indikatorprodukte sind wieder mit i1, i2 und i3 bezeichnet und in der Datenmatrix ‘subdata3’ verfügbar.
head(subdata3)## F1 F2 F3 D7 D8 D9 F4 F5 F6 i1 i2 i3
## 1 4 4 5 4 4 4 4 4 3 0.01403958 0.04043002 -0.135164071
## 2 4 4 4 4 4 4 4 4 3 0.01403958 0.04043002 -0.005595965
## 4 4 4 4 4 5 4 4 4 3 0.01403958 -0.08249357 -0.005595965
## 5 3 3 3 3 3 3 1 1 3 1.26985353 1.49225726 1.080782773
## 6 5 5 5 5 5 5 5 5 5 0.75822563 0.58860277 0.908025298
## 8 4 4 3 4 4 5 2 2 3 0.01403958 0.04043002 -0.832838490Im ‘Lavaan’-Modell ist der latente Interaktionsterm mit ‘Interaktion’ benannt und als zusätzliche erklärende Variable in das Strukturmodell eingefügt.
library ('lavaan')
Model5 <- '
Kombi =~ F1 + F2 + F3
Vertrauen =~ D7 + D8 + D9
Interaktion =~ i1 + i2 + i3
MKC =~ F4 + F5 + F6
MKC ~ Kombi + Vertrauen + Interaktion'
Model5_FIT <- sem(Model5,subdata3, meanstructure=TRUE)
summary (Model5_FIT)## lavaan 0.6-10 ended normally after 38 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 42
##
## Number of observations 301
##
## Model Test User Model:
##
## Test statistic 141.579
## Degrees of freedom 48
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## Kombi =~
## F1 1.000
## F2 1.073 0.077 13.931 0.000
## F3 1.020 0.078 13.144 0.000
## Vertrauen =~
## D7 1.000
## D8 1.204 0.092 13.118 0.000
## D9 1.316 0.102 12.849 0.000
## Interaktion =~
## i1 1.000
## i2 1.093 0.137 7.961 0.000
## i3 1.245 0.164 7.582 0.000
## MKC =~
## F4 1.000
## F5 1.043 0.067 15.563 0.000
## F6 0.696 0.057 12.299 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## MKC ~
## Kombi 0.719 0.110 6.554 0.000
## Vertrauen 0.280 0.118 2.378 0.017
## Interaktion 0.300 0.122 2.460 0.014
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## Kombi ~~
## Vertrauen 0.241 0.038 6.368 0.000
## Interaktion -0.141 0.034 -4.099 0.000
## Vertrauen ~~
## Interaktion -0.134 0.030 -4.450 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .F1 4.080 0.053 77.038 0.000
## .F2 4.123 0.054 76.026 0.000
## .F3 3.957 0.055 71.375 0.000
## .D7 4.176 0.051 81.881 0.000
## .D8 4.329 0.049 88.980 0.000
## .D9 4.130 0.057 72.998 0.000
## .i1 0.225 0.049 4.549 0.000
## .i2 0.262 0.049 5.340 0.000
## .i3 0.418 0.071 5.910 0.000
## .F4 3.462 0.069 50.086 0.000
## .F5 3.462 0.064 53.822 0.000
## .F6 3.738 0.058 64.708 0.000
## Kombi 0.000
## Vertrauen 0.000
## Interaktion 0.000
## .MKC 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .F1 0.318 0.037 8.654 0.000
## .F2 0.279 0.037 7.546 0.000
## .F3 0.378 0.041 9.132 0.000
## .D7 0.397 0.038 10.520 0.000
## .D8 0.153 0.028 5.466 0.000
## .D9 0.295 0.039 7.605 0.000
## .i1 0.403 0.050 8.119 0.000
## .i2 0.324 0.051 6.372 0.000
## .i3 0.984 0.101 9.775 0.000
## .F4 0.485 0.059 8.185 0.000
## .F5 0.209 0.050 4.189 0.000
## .F6 0.543 0.050 10.811 0.000
## Kombi 0.526 0.069 7.636 0.000
## Vertrauen 0.385 0.058 6.609 0.000
## Interaktion 0.335 0.063 5.346 0.000
## .MKC 0.607 0.082 7.415 0.000In diesem Modell finden wir drei signifikante Pfadkoeffizienten vor. Im Vergleich zum Modell ohne Interaktionsterm werden die Pfadkoeffizienten von Wissenskombination auf die gemeinsame Wissensbildung und Vertrauen auf die gemeinsame Wissensbildung etwas höher geschätzt.
Dies führt unter anderem dazu, dass der Pfadkoeffizient von interorganisationalem Vertrauen auf die gemeinsame Wissensbildung in diesem Modell mit einem p-Wert kleiner als 0.05 signifikant ausfällt.
Diese Veränderung ist dadurch verursacht, dass der Einschluss des Interaktionsterms in die Modellschätzung die Interpretation der Pfadkoeffizienten der latenten Variablen ändert.
So stellt der Wert des Pfadkoeffizienten von Vertrauen auf gemeinsame Wissensbildung den Einfluss von Vertrauen auf die gemeinsame Wissensbildung für die Situation dar, in welcher der Wert von Wissenskombination gleich Null ist.
Aufgrund der vorgenommenen Mittelwertzentrierung steht die Null in diesem Zusammenhang für durchschnittliche Werte.
Die Art der Interpretation wechselt also durch die Hinzunahme des Interaktionterms von einem unkonditionalen zu einem konditionalen Effekt, gelegentlich auch als First-order-Effekt bezeichnet.
Für unsere Hypothesen ergibt sich, dass die erste Hypothese, nach welcher Wissenskombination und Vertrauen in Hinblick auf die gemeinsame Wissensbildung interagieren erste Unterstützung erhält.
Wie schon aus den bisherigen Betrachtungen von Interaktionseffekten bekannt, bedarf es zu Bestätigung der zweiten Hypothese weiterer Betrachtungen und Spezifikationen des Modells.
Um dies zu veranschaulichen, möchte ich eine andere Darstellungsform verwenden. Die Interaktion ‘Wissenskombination x Vertrauen’ ist hier als eigenständige latente Variable dargestellt und ihre Indikatoren bilden die drei Produktterme D4xD7, D5xD8 und D6xD9.
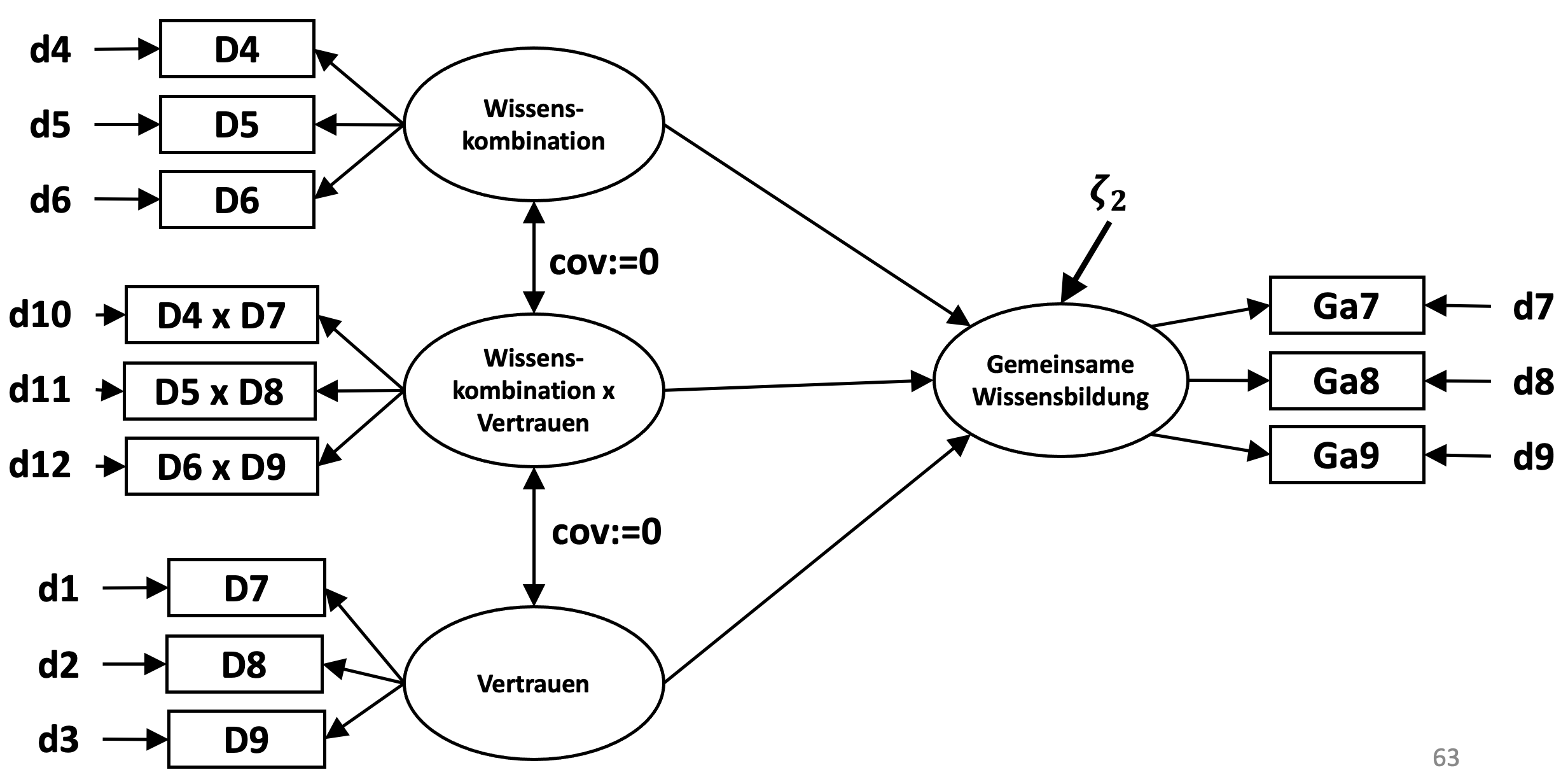
Eine zentrale und bislang unberücksichtigt gebliebene Annahme bei der Testung von Interaktionseffekten ist die Orthogonalität des Interaktionsterms und der exogenen latenten Variablen, hier dargestellt als Kovarianz mit einem zugewiesenem Wert von Null (Little, Bovaird & Widaman, 2006).
Im ‘Lavaan’-Modell bedarf es dafür zwei zusätzlicher Zeilen, in denen die Kovarianzen zwischen dem latenten Interaktionsterm und der latenten Variable Wissenskombination bzw. der latenten Variable Vertrauen auf Null gesetzt werden.
Um die Kovarianz zu bestimmen verwenden wird die Doppel-Tilde gefolgt von der Spezifikation “Null mal” und der latenten Variable Kombi bzw. in der nächsten Zeile gefolgt von der latenten Variable Vertrauen.
Darüber hinaus werden in den nächsten Zeilen noch ein paar Festlegungen getroffen, die es in der Folge ermöglichen, die geschätzten Zusammenhänge zwischen der exogenen latenten Variable und der endogenen latenten Variable für verschiedene Ausprägungen des Moderators mit der Programm-Bibiothek ‘semTools’ zu bestimmen und grafisch darzustellen.
Model5_1 <- '
Kombi =~ F1 + F2 + F3
Vertrauen =~ D7 + D8 + D9
Interaktion =~ i1 + i2 + i3
MKC =~ F4 + F5 + F6
MKC ~ Kombi + Vertrauen + Interaktion
# die Kovarianz zwischen dem latenten Interaktionsterm und den
# latenten Variablen, aus denen er gebildet wurde, werden auf
# Null gesetzt. D.h. der Interaktionsterm soll orthogonal zu
# den latenten Variablen sein.
Interaktion ~~ 0*Kombi
Interaktion ~~ 0*Vertrauen
# die Schnittpunkte/ Intercepts des jeweils ersten Indikators
# der latenten Variablen wird auf einen Wert von Null festgelegt
F1 ~ 0*1
D7 ~ 0*1
i1 ~ 0*1
F4 ~ 0*1
# die Mittelwerte der latenten Variablen und des latenten
# Interaktionsterms werden frei geschätzt, ausgedrückt
# durch "~ NA*1"
Kombi ~ NA*1 # der Mittelwert der latenten Variable
# soll frei geschätzt werden
Vertrauen ~ NA*1
Interaktion ~ NA*1
MKC ~ NA*1
'Diese Festlegungen betreffen die Schnittpunkte des jeweils ersten Indikators pro latenter Variable, die jeweils auf einen Wert von Null festgelegt werden und es wird festgelegt, dass die Mittelwerte aller latenten Variablen inklusive des latenten Interaktionsterms im Modell frei geschätzt werden sollen (vgl. z.B. Theresa Hoffmann & Mayer, 2022).
Die resultierenden Schätzungen für die Pfadkoeffizienten und die damit verbundenen p-Werte unterscheiden sich nur minimal von denen aus dem Interaktionsmodell ohne die explizite Restriktion der Orthogonalität.
## lavaan 0.6-10 ended normally after 81 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 40
##
## Number of observations 301
##
## Model Test User Model:
##
## Test statistic 174.510
## Degrees of freedom 50
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Kombi =~
## F1 1.000 0.728 0.792
## F2 1.067 0.077 13.922 0.000 0.777 0.826
## F3 1.014 0.077 13.143 0.000 0.738 0.768
## Vertrauen =~
## D7 1.000 0.623 0.705
## D8 1.198 0.091 13.113 0.000 0.747 0.885
## D9 1.310 0.102 12.871 0.000 0.817 0.832
## Interaktion =~
## i1 1.000 0.606 0.705
## i2 1.057 0.147 7.172 0.000 0.640 0.752
## i3 1.090 0.154 7.063 0.000 0.660 0.539
## MKC =~
## F4 1.000 0.997 0.820
## F5 1.043 0.065 16.166 0.000 1.040 0.916
## F6 0.696 0.055 12.619 0.000 0.694 0.686
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## MKC ~
## Kombi 0.698 0.106 6.578 0.000 0.509 0.509
## Vertrauen 0.247 0.112 2.202 0.028 0.154 0.154
## Interaktion 0.240 0.101 2.377 0.017 0.146 0.146
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Kombi ~~
## Interaktion 0.000 0.000 0.000
## Vertrauen ~~
## Interaktion 0.000 0.000 0.000
## Kombi ~~
## Vertrauen 0.243 0.038 6.380 0.000 0.536 0.536
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .F1 0.000 0.000 0.000
## .D7 0.000 0.000 0.000
## .i1 0.000 0.000 0.000
## .F4 0.000 0.000 0.000
## Kombi 4.080 0.053 77.038 0.000 5.604 5.604
## Vertrauen 4.176 0.051 81.881 0.000 6.698 6.698
## Interaktion 0.225 0.049 4.549 0.000 0.372 0.372
## .MKC -0.468 0.448 -1.045 0.296 -0.470 -0.470
## .F2 -0.231 0.316 -0.732 0.464 -0.231 -0.246
## .F3 -0.181 0.318 -0.567 0.571 -0.181 -0.188
## .D8 -0.672 0.385 -1.749 0.080 -0.672 -0.797
## .D9 -1.340 0.429 -3.125 0.002 -1.340 -1.365
## .i2 0.024 0.059 0.403 0.687 0.024 0.028
## .i3 0.172 0.079 2.182 0.029 0.172 0.140
## .F5 -0.149 0.229 -0.651 0.515 -0.149 -0.131
## .F6 1.328 0.198 6.720 0.000 1.328 1.312
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .F1 0.314 0.037 8.545 0.000 0.314 0.372
## .F2 0.282 0.037 7.561 0.000 0.282 0.318
## .F3 0.380 0.042 9.133 0.000 0.380 0.411
## .D7 0.394 0.038 10.457 0.000 0.394 0.504
## .D8 0.155 0.029 5.421 0.000 0.155 0.217
## .D9 0.297 0.039 7.532 0.000 0.297 0.308
## .i1 0.371 0.056 6.678 0.000 0.371 0.503
## .i2 0.314 0.058 5.430 0.000 0.314 0.434
## .i3 1.066 0.104 10.291 0.000 1.066 0.710
## .F4 0.485 0.059 8.253 0.000 0.485 0.328
## .F5 0.209 0.049 4.247 0.000 0.209 0.162
## .F6 0.543 0.050 10.825 0.000 0.543 0.530
## Kombi 0.530 0.069 7.669 0.000 1.000 1.000
## Vertrauen 0.389 0.059 6.638 0.000 1.000 1.000
## Interaktion 0.367 0.070 5.257 0.000 1.000 1.000
## .MKC 0.608 0.081 7.549 0.000 0.611 0.611Wie schon angesprochen besteht in diesem Fall ein entscheidender Vorteil in der Möglichkeit, die Ergebnisse mit der Programm-Bibiothek ‘semTools’ genauer zu betrachten und darzustellen.
In diesem konkreten Beispiel werden die drei Prädiktoren ‘Kombi’, ‘Vertrauen’ und ‘Interaktion’ einbezogen und die gemeinsame Wissensbildung abgekürzt mit ‘MKC’ als endogene, also abhängige Variable angesehen.
‘Vertrauen’ soll in der Interaktion als Moderator betrachtet werden. Im Ergebnis wollen wir die Zusammenhänge von Wissenskombination auf die Wissensbildung bei geringem, mittlerem und hohen Vertrauen bestimmen. Hierfür geben wir den Wert -1 für geringes, 0 für mittleres bzw. 1 für hohes Vertrauen an.
## $SimpleIntcept
## Vertrauen est se z pvalue
## 1 -1 -0.715 0.517 -1.382 0.167
## 2 0 -0.468 0.448 -1.045 0.296
## 3 1 -0.222 0.399 -0.556 0.578
##
## $SimpleSlope
## Vertrauen est se z pvalue
## 1 -1 0.458 0.144 3.174 0.002
## 2 0 0.698 0.106 6.578 0.000
## 3 1 0.938 0.149 6.309 0.000Demnach weist Wissenskombination bei geringem Vertrauen in den Kooperationspartner einen Zusammenhang mit gemeinsamer Wissensbildung in Höhe von 0.458 auf. Im Kontext hohen Vertrauens wächst dieser Zusammenhang auf einen Wert in Höhe von 0.938. Weisen wir dieses Ergebnis dem Label ‘result2wayMC’ zu können wir das Ergebnis mit der Anweisung ‘plotProbe’ darstellen.
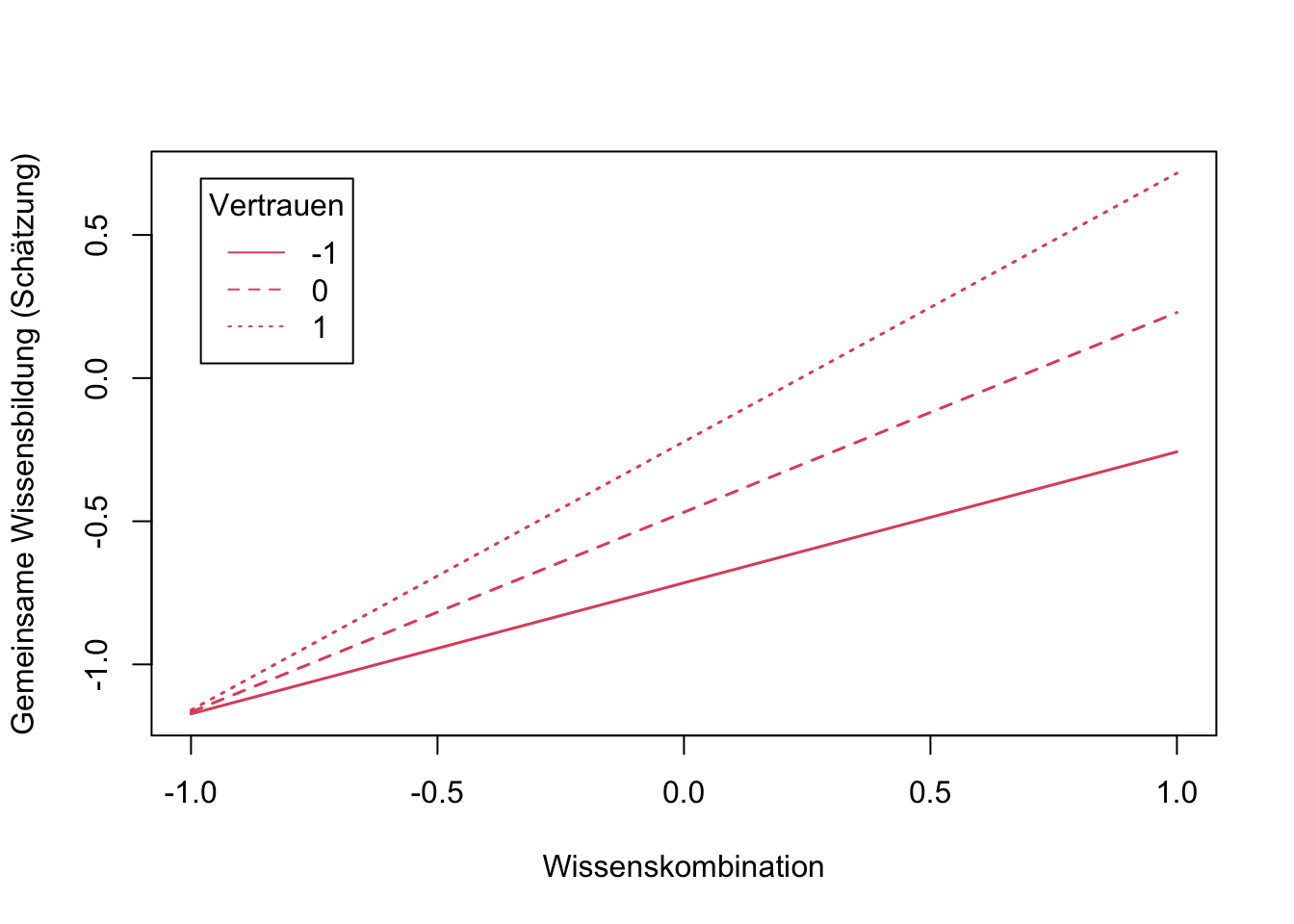
Dieses Vorgehen kommt dem gegenwärtigen Standard an die Modellierung latenter Interaktionen schon recht nahe.
Zwei Weiterentwicklungen werde ich in einem noch folgenden Video vorstellen, die doppelte Mittelwertzentrierung und den Residual-basierten Ansatz bei der Produktindikator-Bildung.
Für beide Methoden kann die Programm-Bibliothek ‘semTools’ verwendet werden. Bei der doppelten Mittelwertzentrierung werden die Indikatoren wie wir es bereits kennen gelernt haben vor der Produktbildung zentriert und im Anschluss an die Produktbildung werden die resultierenden Indikatorprodukte noch einmal einer Mittelwertzentriert unterzogen.
Dies kann einfach gesagt eine Verzerrung des Produktterms durch hohe Kovarianz der latenten Variablen, eine unterschiedliche Varianz ihrer Indikatoren und einer damit verbundene Schiefe der Verteilungen reduzieren.
Vorerst und abschließend in diesem Beitrag möchte ich jedoch noch einmal die Möglichkeit aufzeigen, wie unsere zweite Hypothese: Das der positive Einfluss der Wissenskombination auf die gemeinsame Wissensbildung bei hohem Vertrauen signifikant stärker ausgeprägt ist als bei geringem Vertrauen.
Wir hatten zuletzt mit Hilfe der Programm-Bibiothek ‘semTools’ die marginalen Zusammenhänge bestimmt. Bei geringem Vertrauen beträgt der Zusammenhang zwischen Wissenskombination und gemeinsamer Wissensbildung 0.458, während dieser Zusammenhang bei hohem Vertrauen 0.938 beträgt.
Wie wir bestimmen können, ob dieser Unterschied auch signifikant ist, hatten wir schon in einem früheren Beitrag im Kontext der Pfadmodelle aufgezeigt. An dieser Stelle will ich dieses Vorgehen noch einmal wiederholen.
Ausgehend von der Gleichung des marginalen Effektes ergibt sich der konditionale Effekt von Wissenskombination auf die gemeinsame Wissensbildung aus der Summe des Pfadkoeffizienten für Wissenskombination (gamma1) und dem Produkt des Pfadkoeffizienten für den Interaktionsterm (gamma3) und der Ausprägung von Vertrauen.
'MKC ~ gamma1 * Kombi + Vertrauen + gamma3 * Interaktion
ME_gerVert := gamma1 + (gamma3*(-1))
ME_hohVert := gamma1 + (gamma3*(+1))'## [1] "MKC ~ gamma1 * Kombi + Vertrauen + gamma3 * Interaktion\n ME_gerVert := gamma1 + (gamma3*(-1))\n ME_hohVert := gamma1 + (gamma3*(+1))"Wir bestimmen also direkt im Modell den marginalen Zusammenhang für Wissenskombination bei geringem und bei hohem Vertrauen, wobei wir wieder -1 für geringes und +1 für hohes Vertrauen angeben. Darüber hinaus bilden wir die Differenz aus diesen beiden Werten.
'ME_Diff := ME_gerVert - ME_hohVert'## [1] "ME_Diff := ME_gerVert - ME_hohVert"Hier die gesamte Syntax:
Model5_2 <- '
Kombi =~ F1 + F2 + F3
Vertrauen =~ D7 + D8 + D9
Interaktion =~ i1 + i2 + i3
MKC =~ F4 + F5 + F6
MKC ~ gamma1 * Kombi + Vertrauen + gamma3 * Interaktion
ME_gerVert := gamma1 + (gamma3*(-1))
ME_hohVert := gamma1 + (gamma3*(+1))
ME_Diff := ME_gerVert - ME_hohVert
Interaktion ~~ 0*Kombi
Interaktion ~~ 0*Vertrauen
F1 ~ 0*1
D7 ~ 0*1
i1 ~ 0*1
F4 ~ 0*1
Kombi ~ NA*1 # der Mittelwert der latenten Variable
# soll frei geschätzt werden
Vertrauen ~ NA*1
Interaktion ~ NA*1
MKC ~ NA*1
'
Model5_2FIT <- sem(Model5_2,subdata3, meanstructure=TRUE)
summary (Model5_2FIT, standardized=TRUE)## lavaan 0.6-10 ended normally after 81 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 40
##
## Number of observations 301
##
## Model Test User Model:
##
## Test statistic 174.510
## Degrees of freedom 50
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Kombi =~
## F1 1.000 0.728 0.792
## F2 1.067 0.077 13.922 0.000 0.777 0.826
## F3 1.014 0.077 13.143 0.000 0.738 0.768
## Vertrauen =~
## D7 1.000 0.623 0.705
## D8 1.198 0.091 13.113 0.000 0.747 0.885
## D9 1.310 0.102 12.871 0.000 0.817 0.832
## Interaktion =~
## i1 1.000 0.606 0.705
## i2 1.057 0.147 7.172 0.000 0.640 0.752
## i3 1.090 0.154 7.063 0.000 0.660 0.539
## MKC =~
## F4 1.000 0.997 0.820
## F5 1.043 0.065 16.166 0.000 1.040 0.916
## F6 0.696 0.055 12.619 0.000 0.694 0.686
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## MKC ~
## Kombi (gmm1) 0.698 0.106 6.578 0.000 0.509 0.509
## Vertran 0.247 0.112 2.202 0.028 0.154 0.154
## Intrktn (gmm3) 0.240 0.101 2.377 0.017 0.146 0.146
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Kombi ~~
## Interaktion 0.000 0.000 0.000
## Vertrauen ~~
## Interaktion 0.000 0.000 0.000
## Kombi ~~
## Vertrauen 0.243 0.038 6.380 0.000 0.536 0.536
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .F1 0.000 0.000 0.000
## .D7 0.000 0.000 0.000
## .i1 0.000 0.000 0.000
## .F4 0.000 0.000 0.000
## Kombi 4.080 0.053 77.038 0.000 5.604 5.604
## Vertrauen 4.176 0.051 81.881 0.000 6.698 6.698
## Interaktion 0.225 0.049 4.549 0.000 0.372 0.372
## .MKC -0.468 0.448 -1.045 0.296 -0.470 -0.470
## .F2 -0.231 0.316 -0.732 0.464 -0.231 -0.246
## .F3 -0.181 0.318 -0.567 0.571 -0.181 -0.188
## .D8 -0.672 0.385 -1.749 0.080 -0.672 -0.797
## .D9 -1.340 0.429 -3.125 0.002 -1.340 -1.365
## .i2 0.024 0.059 0.403 0.687 0.024 0.028
## .i3 0.172 0.079 2.182 0.029 0.172 0.140
## .F5 -0.149 0.229 -0.651 0.515 -0.149 -0.131
## .F6 1.328 0.198 6.720 0.000 1.328 1.312
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .F1 0.314 0.037 8.545 0.000 0.314 0.372
## .F2 0.282 0.037 7.561 0.000 0.282 0.318
## .F3 0.380 0.042 9.133 0.000 0.380 0.411
## .D7 0.394 0.038 10.457 0.000 0.394 0.504
## .D8 0.155 0.029 5.421 0.000 0.155 0.217
## .D9 0.297 0.039 7.532 0.000 0.297 0.308
## .i1 0.371 0.056 6.678 0.000 0.371 0.503
## .i2 0.314 0.058 5.430 0.000 0.314 0.434
## .i3 1.066 0.104 10.291 0.000 1.066 0.710
## .F4 0.485 0.059 8.253 0.000 0.485 0.328
## .F5 0.209 0.049 4.247 0.000 0.209 0.162
## .F6 0.543 0.050 10.825 0.000 0.543 0.530
## Kombi 0.530 0.069 7.669 0.000 1.000 1.000
## Vertrauen 0.389 0.059 6.638 0.000 1.000 1.000
## Interaktion 0.367 0.070 5.257 0.000 1.000 1.000
## .MKC 0.608 0.081 7.549 0.000 0.611 0.611
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ME_gerVert 0.458 0.144 3.174 0.002 0.364 0.364
## ME_hohVert 0.938 0.149 6.309 0.000 0.655 0.655
## ME_Diff -0.480 0.202 -2.377 0.017 -0.291 -0.291Während uns die zwei Zusammenhangsmaße bei geringem und hohen Vertrauen schon bekannt waren, resultiert hier zusätzlich die Differenz der beiden Koeffizienten in Höhe von -0.48 mit einem p-Wert von 0.017.
Dies unterstützt die Hypothese, dass der positive Zusammenhang zwischen Wissenskombination und gemeinsamer Wissensbildung durch hohes Vertrauen gefördert wird.
Literatur
Im Plot zeichnet sich eine notwendige Bedingung dadurch aus, dass die Datenpunkte vorwiegend rechts unter der Diagonalen auftreten. ↩︎